SISTEMAS DE CONTROLE II
Dado o sistema a seguir, calcule o ganho de K.
%7D%5C%5C%7Bx%7D_%7B%7B%7B2%7D%7D%7D%26%7B%5Cleft(%7Bk%7D%2B%7B1%7D%5Cright)%7D%7D%5Cright%5D%7D%3D%7B%5Cleft%5B%5Cmatrix%7B%7B0%7D%26%7B1%7D%5C%5C-%7B0.16%7D%26-%7B1%7D%7D%5Cright%5D%7D%7B%5Cleft%5Clbrace%5Cmatrix%7B%7Bx%7D_%7B%7B%7B1%7D%7D%7D%26%7B%5Cleft(%7Bk%7D%5Cright)%7D%5C%5C%7Bx%7D_%7B%7B%7B2%7D%7D%7D%26%7B%5Cleft(%7Bk%7D%5Cright)%7D%7D%5Cright%5Crbrace%7D%2B%7B%5Cleft%5B%5Cmatrix%7B%7B0%7D%5C%5C%7B1%7D%7D%5Cright%5D%7D%7Bu%7D%7B%5Cleft(%7Bk%7D%5Cright)%7D "[[x_(1),(k+1)],[x_(2),(k+1)]]=[[0,1],[-0.16,-1]]{[x_(1),(k)],[x_(2),(k)]}+[[0],[1]] u(k)")
%7D%3D%7B%5Cleft%5B%5Cmatrix%7B%7B1%7D%26%7B0%7D%7D%5Cright%5D%7D%7B%5Cleft%5Clbrace%5Cmatrix%7B%7Bx%7D_%7B%7B%7B1%7D%7D%7D%26%7B%5Cleft(%7Bk%7D%5Cright)%7D%5C%5C%7Bx%7D_%7B%7B%7B2%7D%7D%7D%26%7B%5Cleft(%7Bk%7D%5Cright)%7D%7D%5Cright%5Crbrace%7D "y(k)=[[1,0]]{[x_(1),(k)],[x_(2),(k)]}")
Sendo os polos da malha:
1
3
0,5
4
2
Um sistema é ____________ no intervalo [to, tf] se qualquer estado inicial x(to) é determinado univocamente através da observação da saída y(t) em um intervalo [to, tf].
Complete a lacuna acima assinalando a alternativa correta.
Observável
Não controlável
Não observável
Controlável
Suportável
Considere uma cadeia de Markov com espaço de estados S = {1, 2, 3} e matriz de transição
A probabilidade condicional de uma transição para o estado 1, dado que o estado inicial era o estado transiente 2, é:
A figura abaixo mostra uma estrutura de controle em malha fechada, onde G(s) corresponde a uma planta que se deseja controlar com uma realimentação de saída através de um compensador H(s). Com base no diagrama, a função de transferência de malha fechada é:
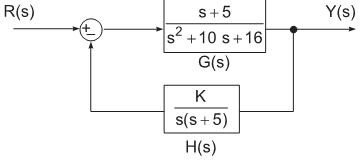
%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%2B%7B10%7D%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B16%7D%7Bs%7D%2B%7BK%7D%7D%7D "(s(s+5))/(s^3+10s^2+16s+K)")
%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B4%7D%7D%2B%7B15%7D%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%2B%7B66%7D%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B80%7D%7Bs%7D%7D%7D "(K(s+5))/(s^4+15s^3+66s^2+80s)")
%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%2B%7B10%7D%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B16%7D%7Bs%7D%2B%7BK%7D%7D%7D "(K(s+5))/(s^3+10s^2+16s+K)")
%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B4%7D%7D%2B%7B15%7D%7B%7Bs%7D%7D%5E%7B%7B3%7D%7D%2B%7B66%7D%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B80%7D%7Bs%7D%2B%7BK%7D%7D%7D "(K(s+51))/(s^4+15s^3+66s^2+80s+K)")
O PID é um caso especial de Lead-lag, o PD comporta-se como _______________, o que afeta sua frequência __________, aumenta seu ângulo de fase, melhorando a estabilidade, há também um aumento da largura de faixa, e o sistema assim fica mais rápido. Tratando do PI ele trabalha com ________________, o que afeta a região de frequência _____________, aumenta seu ganho em baixa frequência, sua precisão é melhorada em regime permanente.
Preencha as lacunas acima e marque a alternativa correspondente.
avanço de fase, baixa, avanço de fase, baixa
atraso de fase, alta, avanço de fase, baixa
avanço de fase, alta, atraso de fase, baixa
atraso de fase, baixa, atraso de fase, baixa
avanço de fase, baixa, atraso de fase, alta
Aplique a técnica de compensação via lugar das raízes para o projeto de um compensador lead para a planta abaixo e atendendo as seguintes especificações de desempenho: ξ = 0,5 , ωn =13,5 rad/s.
Assinale a alternativa correta.
%7D%3D%5Cfrac%7B%7B400%7D%7D%7B%7B%7Bs%7D%7B%5Cleft(%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B30%7D%7Bs%7D%2B%7B200%7D%5Cright)%7D%7D%7D "G(s) = 400/(s(s^2+30s+200)")
Pólo = -30,10 Zero = -5,4
Pólo = -26,39 Zero = -7,5
Pólo = -31,36 Zero = -9,1
Pólo = -25,39 Zero = -7,18
Pólo = -28,52 Zero = -6,5
Obtenha aproximações discretas para o sistema contínuo da figura abaixo, através do método Bilinear ou de Tustin na frequência ωs = 1rad/s. Para o método, calcule a resposta analítica da saída y(k) para k = 0, . . . , 5, quando a entrada u(k) for um degrau unitário. Suponha T = 1s.
Assinale a alternativa correta.
%7D%3D%7B1%7D-%5Cfrac%7B%7B2%7D%7D%7B%7B3%7D%7D%7B%7B%5Cleft(%5Cfrac%7B%7B1%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7Bk%7D%7D "y(k)=1-2/3(1/3)^k")
%7D%3D%5Cfrac%7B%7B2%7D%7D%7B%7B3%7D%7D%7B%7B%5Cleft(%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7Bk%7D%7D "y(k)=2/3(4/3)^k")
%7D%3D%5Cfrac%7B%7B2%7D%7D%7B%7B3%7D%7D%7B%7B%5Cleft(%5Cfrac%7B%7B1%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7Bk%7D%7D "y(k)=2/3(1/3)^k")
%7D%3D%7B1%7D-%5Cfrac%7B%7B5%7D%7D%7B%7B3%7D%7D%7B%7B%5Cleft(%5Cfrac%7B%7B1%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7Bk%7D%7D "y(k)=1-5/3(1/3)^k")
%7D%3D%7B1%7D-%5Cfrac%7B%7B2%7D%7D%7B%7B3%7D%7D%7B%7B%5Cleft(%5Cfrac%7B%7B4%7D%7D%7B%7B3%7D%7D%5Cright)%7D%7D%5E%7B%7Bk%7D%7D "y(k)=1-2/3(4/3)^k")
A seguir temos alguns termos relativos a quantidades presentes em sistemas de controle. Os valores dessas quantidades geralmente são funções da variável independente tempo.
A - Variável (ou comando) de referência.
B - Variável controlada (ou regulada).
C - Variável de controle (ou manipulada).
D - Controlador (ou compensador).
( ) É qualquer sistema conectado à planta e responsável pela definição da variável de controle, visando fazer com que a variável controlada responda de acordo com o especificado pela variável de referência.
( ) É a quantidade determinada pela ação de um controlador. A variável de controle é geralmente identificada como a variável de entrada da planta.
( ) É qualquer variável que se deseja controlar. A variável controlada é geralmente representada pela variável de saída do sistema de controle.
( ) Serve de referência (no sentido de comportamento desejado) para a variável a ser controlada.
Completa corretamente a sequência a alternativa:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A
Dada a equação diferencial de 3a ordem x’’’+ x’’ + 2x’ + x = 2f(t), sua representação no espaço de estados é:
1
3
0,5
4
2
Um sistema é ____________ no intervalo [to, tf] se qualquer estado inicial x(to) é determinado univocamente através da observação da saída y(t) em um intervalo [to, tf].
Complete a lacuna acima assinalando a alternativa correta.
Observável
Não controlável
Não observável
Controlável
Suportável
Considere uma cadeia de Markov com espaço de estados S = {1, 2, 3} e matriz de transição
A probabilidade condicional de uma transição para o estado 1, dado que o estado inicial era o estado transiente 2, é:
A figura abaixo mostra uma estrutura de controle em malha fechada, onde G(s) corresponde a uma planta que se deseja controlar com uma realimentação de saída através de um compensador H(s). Com base no diagrama, a função de transferência de malha fechada é:
O PID é um caso especial de Lead-lag, o PD comporta-se como _______________, o que afeta sua frequência __________, aumenta seu ângulo de fase, melhorando a estabilidade, há também um aumento da largura de faixa, e o sistema assim fica mais rápido. Tratando do PI ele trabalha com ________________, o que afeta a região de frequência _____________, aumenta seu ganho em baixa frequência, sua precisão é melhorada em regime permanente.
Preencha as lacunas acima e marque a alternativa correspondente.
avanço de fase, baixa, avanço de fase, baixa
atraso de fase, alta, avanço de fase, baixa
avanço de fase, alta, atraso de fase, baixa
atraso de fase, baixa, atraso de fase, baixa
avanço de fase, baixa, atraso de fase, alta
Aplique a técnica de compensação via lugar das raízes para o projeto de um compensador lead para a planta abaixo e atendendo as seguintes especificações de desempenho: ξ = 0,5 , ωn =13,5 rad/s.
Assinale a alternativa correta.
Pólo = -30,10 Zero = -5,4
Pólo = -26,39 Zero = -7,5
Pólo = -31,36 Zero = -9,1
Pólo = -25,39 Zero = -7,18
Pólo = -28,52 Zero = -6,5
Obtenha aproximações discretas para o sistema contínuo da figura abaixo, através do método Bilinear ou de Tustin na frequência ωs = 1rad/s. Para o método, calcule a resposta analítica da saída y(k) para k = 0, . . . , 5, quando a entrada u(k) for um degrau unitário. Suponha T = 1s.
Assinale a alternativa correta.
A seguir temos alguns termos relativos a quantidades presentes em sistemas de controle. Os valores dessas quantidades geralmente são funções da variável independente tempo.
A - Variável (ou comando) de referência.
B - Variável controlada (ou regulada).
C - Variável de controle (ou manipulada).
D - Controlador (ou compensador).
( ) É qualquer sistema conectado à planta e responsável pela definição da variável de controle, visando fazer com que a variável controlada responda de acordo com o especificado pela variável de referência.
( ) É a quantidade determinada pela ação de um controlador. A variável de controle é geralmente identificada como a variável de entrada da planta.
( ) É qualquer variável que se deseja controlar. A variável controlada é geralmente representada pela variável de saída do sistema de controle.
( ) Serve de referência (no sentido de comportamento desejado) para a variável a ser controlada.
Completa corretamente a sequência a alternativa:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A
Dada a equação diferencial de 3a ordem x’’’+ x’’ + 2x’ + x = 2f(t), sua representação no espaço de estados é:
Observável
Não controlável
Não observável
Controlável
Suportável
Considere uma cadeia de Markov com espaço de estados S = {1, 2, 3} e matriz de transição
A probabilidade condicional de uma transição para o estado 1, dado que o estado inicial era o estado transiente 2, é:
A figura abaixo mostra uma estrutura de controle em malha fechada, onde G(s) corresponde a uma planta que se deseja controlar com uma realimentação de saída através de um compensador H(s). Com base no diagrama, a função de transferência de malha fechada é:
O PID é um caso especial de Lead-lag, o PD comporta-se como _______________, o que afeta sua frequência __________, aumenta seu ângulo de fase, melhorando a estabilidade, há também um aumento da largura de faixa, e o sistema assim fica mais rápido. Tratando do PI ele trabalha com ________________, o que afeta a região de frequência _____________, aumenta seu ganho em baixa frequência, sua precisão é melhorada em regime permanente.
Preencha as lacunas acima e marque a alternativa correspondente.
avanço de fase, baixa, avanço de fase, baixa
atraso de fase, alta, avanço de fase, baixa
avanço de fase, alta, atraso de fase, baixa
atraso de fase, baixa, atraso de fase, baixa
avanço de fase, baixa, atraso de fase, alta
Aplique a técnica de compensação via lugar das raízes para o projeto de um compensador lead para a planta abaixo e atendendo as seguintes especificações de desempenho: ξ = 0,5 , ωn =13,5 rad/s.
Assinale a alternativa correta.
Pólo = -30,10 Zero = -5,4
Pólo = -26,39 Zero = -7,5
Pólo = -31,36 Zero = -9,1
Pólo = -25,39 Zero = -7,18
Pólo = -28,52 Zero = -6,5
Obtenha aproximações discretas para o sistema contínuo da figura abaixo, através do método Bilinear ou de Tustin na frequência ωs = 1rad/s. Para o método, calcule a resposta analítica da saída y(k) para k = 0, . . . , 5, quando a entrada u(k) for um degrau unitário. Suponha T = 1s.
Assinale a alternativa correta.
A seguir temos alguns termos relativos a quantidades presentes em sistemas de controle. Os valores dessas quantidades geralmente são funções da variável independente tempo.
A - Variável (ou comando) de referência.
B - Variável controlada (ou regulada).
C - Variável de controle (ou manipulada).
D - Controlador (ou compensador).
( ) É qualquer sistema conectado à planta e responsável pela definição da variável de controle, visando fazer com que a variável controlada responda de acordo com o especificado pela variável de referência.
( ) É a quantidade determinada pela ação de um controlador. A variável de controle é geralmente identificada como a variável de entrada da planta.
( ) É qualquer variável que se deseja controlar. A variável controlada é geralmente representada pela variável de saída do sistema de controle.
( ) Serve de referência (no sentido de comportamento desejado) para a variável a ser controlada.
Completa corretamente a sequência a alternativa:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A
Dada a equação diferencial de 3a ordem x’’’+ x’’ + 2x’ + x = 2f(t), sua representação no espaço de estados é:
A figura abaixo mostra uma estrutura de controle em malha fechada, onde G(s) corresponde a uma planta que se deseja controlar com uma realimentação de saída através de um compensador H(s). Com base no diagrama, a função de transferência de malha fechada é:
O PID é um caso especial de Lead-lag, o PD comporta-se como _______________, o que afeta sua frequência __________, aumenta seu ângulo de fase, melhorando a estabilidade, há também um aumento da largura de faixa, e o sistema assim fica mais rápido. Tratando do PI ele trabalha com ________________, o que afeta a região de frequência _____________, aumenta seu ganho em baixa frequência, sua precisão é melhorada em regime permanente.
Preencha as lacunas acima e marque a alternativa correspondente.
avanço de fase, baixa, avanço de fase, baixa
atraso de fase, alta, avanço de fase, baixa
avanço de fase, alta, atraso de fase, baixa
atraso de fase, baixa, atraso de fase, baixa
avanço de fase, baixa, atraso de fase, alta
Aplique a técnica de compensação via lugar das raízes para o projeto de um compensador lead para a planta abaixo e atendendo as seguintes especificações de desempenho: ξ = 0,5 , ωn =13,5 rad/s.
Assinale a alternativa correta.
Pólo = -30,10 Zero = -5,4
Pólo = -26,39 Zero = -7,5
Pólo = -31,36 Zero = -9,1
Pólo = -25,39 Zero = -7,18
Pólo = -28,52 Zero = -6,5
Obtenha aproximações discretas para o sistema contínuo da figura abaixo, através do método Bilinear ou de Tustin na frequência ωs = 1rad/s. Para o método, calcule a resposta analítica da saída y(k) para k = 0, . . . , 5, quando a entrada u(k) for um degrau unitário. Suponha T = 1s.
Assinale a alternativa correta.
A seguir temos alguns termos relativos a quantidades presentes em sistemas de controle. Os valores dessas quantidades geralmente são funções da variável independente tempo.
A - Variável (ou comando) de referência.
B - Variável controlada (ou regulada).
C - Variável de controle (ou manipulada).
D - Controlador (ou compensador).
( ) É qualquer sistema conectado à planta e responsável pela definição da variável de controle, visando fazer com que a variável controlada responda de acordo com o especificado pela variável de referência.
( ) É a quantidade determinada pela ação de um controlador. A variável de controle é geralmente identificada como a variável de entrada da planta.
( ) É qualquer variável que se deseja controlar. A variável controlada é geralmente representada pela variável de saída do sistema de controle.
( ) Serve de referência (no sentido de comportamento desejado) para a variável a ser controlada.
Completa corretamente a sequência a alternativa:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A
Dada a equação diferencial de 3a ordem x’’’+ x’’ + 2x’ + x = 2f(t), sua representação no espaço de estados é:
O PID é um caso especial de Lead-lag, o PD comporta-se como _______________, o que afeta sua frequência __________, aumenta seu ângulo de fase, melhorando a estabilidade, há também um aumento da largura de faixa, e o sistema assim fica mais rápido. Tratando do PI ele trabalha com ________________, o que afeta a região de frequência _____________, aumenta seu ganho em baixa frequência, sua precisão é melhorada em regime permanente.
Preencha as lacunas acima e marque a alternativa correspondente.
avanço de fase, baixa, avanço de fase, baixa
atraso de fase, alta, avanço de fase, baixa
avanço de fase, alta, atraso de fase, baixa
atraso de fase, baixa, atraso de fase, baixa
avanço de fase, baixa, atraso de fase, alta
Aplique a técnica de compensação via lugar das raízes para o projeto de um compensador lead para a planta abaixo e atendendo as seguintes especificações de desempenho: ξ = 0,5 , ωn =13,5 rad/s.
Assinale a alternativa correta.
Pólo = -30,10 Zero = -5,4
Pólo = -26,39 Zero = -7,5
Pólo = -31,36 Zero = -9,1
Pólo = -25,39 Zero = -7,18
Pólo = -28,52 Zero = -6,5
Obtenha aproximações discretas para o sistema contínuo da figura abaixo, através do método Bilinear ou de Tustin na frequência ωs = 1rad/s. Para o método, calcule a resposta analítica da saída y(k) para k = 0, . . . , 5, quando a entrada u(k) for um degrau unitário. Suponha T = 1s.
Assinale a alternativa correta.
A seguir temos alguns termos relativos a quantidades presentes em sistemas de controle. Os valores dessas quantidades geralmente são funções da variável independente tempo.
A - Variável (ou comando) de referência.
B - Variável controlada (ou regulada).
C - Variável de controle (ou manipulada).
D - Controlador (ou compensador).
( ) É qualquer sistema conectado à planta e responsável pela definição da variável de controle, visando fazer com que a variável controlada responda de acordo com o especificado pela variável de referência.
( ) É a quantidade determinada pela ação de um controlador. A variável de controle é geralmente identificada como a variável de entrada da planta.
( ) É qualquer variável que se deseja controlar. A variável controlada é geralmente representada pela variável de saída do sistema de controle.
( ) Serve de referência (no sentido de comportamento desejado) para a variável a ser controlada.
Completa corretamente a sequência a alternativa:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A
Dada a equação diferencial de 3a ordem x’’’+ x’’ + 2x’ + x = 2f(t), sua representação no espaço de estados é:
avanço de fase, baixa, avanço de fase, baixa
atraso de fase, alta, avanço de fase, baixa
avanço de fase, alta, atraso de fase, baixa
atraso de fase, baixa, atraso de fase, baixa
avanço de fase, baixa, atraso de fase, alta
Aplique a técnica de compensação via lugar das raízes para o projeto de um compensador lead para a planta abaixo e atendendo as seguintes especificações de desempenho: ξ = 0,5 , ωn =13,5 rad/s.
Assinale a alternativa correta.
Pólo = -30,10 Zero = -5,4
Pólo = -26,39 Zero = -7,5
Pólo = -31,36 Zero = -9,1
Pólo = -25,39 Zero = -7,18
Pólo = -28,52 Zero = -6,5
Obtenha aproximações discretas para o sistema contínuo da figura abaixo, através do método Bilinear ou de Tustin na frequência ωs = 1rad/s. Para o método, calcule a resposta analítica da saída y(k) para k = 0, . . . , 5, quando a entrada u(k) for um degrau unitário. Suponha T = 1s.
Assinale a alternativa correta.
A seguir temos alguns termos relativos a quantidades presentes em sistemas de controle. Os valores dessas quantidades geralmente são funções da variável independente tempo.
A - Variável (ou comando) de referência.
B - Variável controlada (ou regulada).
C - Variável de controle (ou manipulada).
D - Controlador (ou compensador).
( ) É qualquer sistema conectado à planta e responsável pela definição da variável de controle, visando fazer com que a variável controlada responda de acordo com o especificado pela variável de referência.
( ) É a quantidade determinada pela ação de um controlador. A variável de controle é geralmente identificada como a variável de entrada da planta.
( ) É qualquer variável que se deseja controlar. A variável controlada é geralmente representada pela variável de saída do sistema de controle.
( ) Serve de referência (no sentido de comportamento desejado) para a variável a ser controlada.
Completa corretamente a sequência a alternativa:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A
Dada a equação diferencial de 3a ordem x’’’+ x’’ + 2x’ + x = 2f(t), sua representação no espaço de estados é:
Pólo = -30,10 Zero = -5,4
Pólo = -26,39 Zero = -7,5
Pólo = -31,36 Zero = -9,1
Pólo = -25,39 Zero = -7,18
Pólo = -28,52 Zero = -6,5
Obtenha aproximações discretas para o sistema contínuo da figura abaixo, através do método Bilinear ou de Tustin na frequência ωs = 1rad/s. Para o método, calcule a resposta analítica da saída y(k) para k = 0, . . . , 5, quando a entrada u(k) for um degrau unitário. Suponha T = 1s.
Assinale a alternativa correta.
A seguir temos alguns termos relativos a quantidades presentes em sistemas de controle. Os valores dessas quantidades geralmente são funções da variável independente tempo.
A - Variável (ou comando) de referência.
B - Variável controlada (ou regulada).
C - Variável de controle (ou manipulada).
D - Controlador (ou compensador).
( ) É qualquer sistema conectado à planta e responsável pela definição da variável de controle, visando fazer com que a variável controlada responda de acordo com o especificado pela variável de referência.
( ) É a quantidade determinada pela ação de um controlador. A variável de controle é geralmente identificada como a variável de entrada da planta.
( ) É qualquer variável que se deseja controlar. A variável controlada é geralmente representada pela variável de saída do sistema de controle.
( ) Serve de referência (no sentido de comportamento desejado) para a variável a ser controlada.
Completa corretamente a sequência a alternativa:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A
Dada a equação diferencial de 3a ordem x’’’+ x’’ + 2x’ + x = 2f(t), sua representação no espaço de estados é:
A seguir temos alguns termos relativos a quantidades presentes em sistemas de controle. Os valores dessas quantidades geralmente são funções da variável independente tempo.
A - Variável (ou comando) de referência.
B - Variável controlada (ou regulada).
C - Variável de controle (ou manipulada).
D - Controlador (ou compensador).
( ) É qualquer sistema conectado à planta e responsável pela definição da variável de controle, visando fazer com que a variável controlada responda de acordo com o especificado pela variável de referência.
( ) É a quantidade determinada pela ação de um controlador. A variável de controle é geralmente identificada como a variável de entrada da planta.
( ) É qualquer variável que se deseja controlar. A variável controlada é geralmente representada pela variável de saída do sistema de controle.
( ) Serve de referência (no sentido de comportamento desejado) para a variável a ser controlada.
Completa corretamente a sequência a alternativa:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A
Dada a equação diferencial de 3a ordem x’’’+ x’’ + 2x’ + x = 2f(t), sua representação no espaço de estados é:
B, C, D e A
A, B, D e C
C, B, D e A
D, C, B e A
A, C, B e A