SISTEMAS DE CONTROLE I
A transformada de Laplace da função
f (t) = te-3t + e-2t cos(2t)
é a função F(s) indicada em uma das alternativa
seguintes. Marque a alternativa correta.
%7D%7D%5E%7B%7B2%7D%7D%7D%2B%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B2%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D) `
`
%7D%7D%5E%7B%7B2%7D%7D%7D%2B%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B2%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B2%7D%7D%7D)
%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D)
%7D%7D%5E%7B%7B2%7D%7D%7D%2B%5Cfrac%7B%7Bs%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B2%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D)
%7D%7D%5E%7B%7B3%7D%7D%7D%2B%5Cfrac%7B%7B%7Bs%7D%2B%7B2%7D%7D%7D%7B%7B%7B%7B%5Cleft(%7Bs%7D%2B%7B2%7D%5Cright)%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%7D%7D) `
`
Deseja-se controlar o sistema abaixo por malha fechada, dessa forma, qual será a variável manipulada (MV) e a variável controlada (PV).

PV : qi(t) e MV : h(t).
PV : qo(t) e MV : qi(t).
PV : h(t) e MV : qo(t).
PV : qi(t) e MV : qo(t).
PV : h(t) e MV : qi(t).
Nas equações apresentas abaixo, c(t) representa possíveis respostas de sistemas de segunda ordem, sujeitos a entrada do tipo degrau unitário.
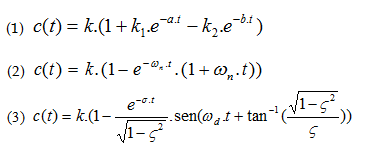
As equações (1), (2) e (3) correspondem, respectivamente, a respostas de sistemas:
Criticamente amortecido, sobreamortecido e subamortecido.
Criticamente amortecido, subamortecido e sobreamortecido.
Sobreamortecido, criticamente amortecido e subamortecido.
Subamortecido, sobreamortecido e criticamente amortecido.
Sobreamortecido, subamortecido e criticamente amortecido.
Considere o lugar das raízes de um sistema de controle com realimentação unitária, e controlador com ganho variável G dado na figura abaixo.
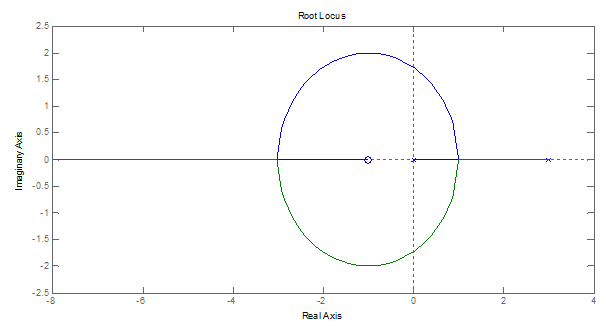
A partir da análise da informações contidas no gráfico, avalie a veracidade das afirmativas a seguir:
I - A equação caraterística do sistema é 1 + G. (s+1)/(s2 -3.s)=0
II - A Função de transferência de malha fechada do sistema de controle é: G(s+1)/(s2 + (G-3).s + G)
III - O lugar das raízes começa nos pólos s=0 e s=3, e terminos zeros s=-1 e s=-∞
IV - Dependendo do valor do parâmetro G, o sistema poderá ser estável ou instável
V - O sistema poderá responder de forma oscilatória ou monótona, dependendo do valor de G
São verdadeiras as afirmativas:
I, II, III, IV e V
II, III e V
II, III e IV
I, III, IV e V
II, III, IV e V
A figura abaixo apresenta o diagrama de um sistema de controle manual de um processo de aquecimento de água em um trocador de calor, usando vapor superaquecido como fonte de energia térmica.
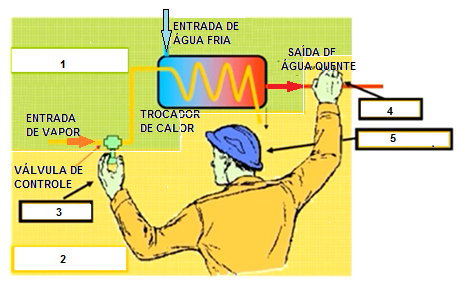
Nos quadros numerados cabem os termos técnicos: processo, sistema de controle, sensor, controlador e atuador.
Nessa ordem, a numeração dos blocos será:
1 - processo; 2 - atuador ; 3 - sensor ; 4 - controlador ; 5 - sistema de controle
1 - processo; 2 - atuador ; 3 - sensor ; 4 - sistema de controle; 5 - controlador
1 - sistema de controle; 2 - processo; 3 - atuador ; 4 - sensor ; 5 - controlador
1 - processo; 2 - atuador ; 3 - sistema de controle; 4 - sensor; 5 - controlador
1 - processo; 2 - sistema de controle; 3 - atuador; 4 - sensor; 5 - controlador
Apresenta-se a seguir uma tabela com pares de transformadas de Laplace de algumas funções.
Porém, em uma mesma linha, pode ser que F(s) não seja a transformada de Laplace de f(t).
Na coluna A foi atribuída uma numeração das funções f(t).
Enumere a coluna B com o número da função f(t), de forma a haver a correta correspondência entre f(t) e F(s),
ou seja, que f(t) e F(s) correspondentes tenham a mesma numeração.
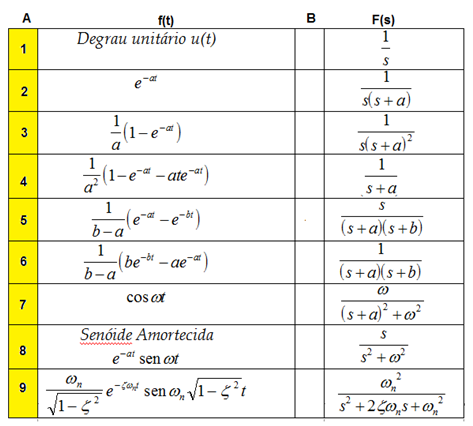
A coluna B, na forma transposta, terá a seguinte sequência numérica:
1 4 3 2 5 6 8 7 9
1 3 4 2 6 5 8 7 9
1 3 4 2 6 5 7 8 9
1 3 4 2 5 6 7 8 9
1 3 4 5 2 6 8 7 9
Na figura abaixo apresenta-se os diagramas elétrico e de blocos de um sistema físico.
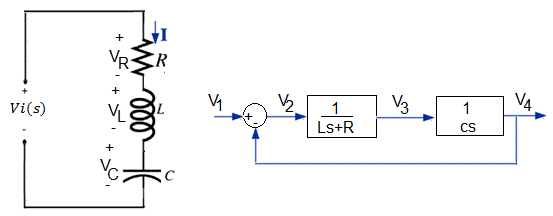
As variáveis V1, V2, V3 e V4 correspondem, respectivamente às variáveis elétricas:
VC ; VR - VL ; I ; Vi
Vi ; VR ; VC ; VL
VL ; Vi - Vc ; I ; VC
Vi ; VR+VL ; I ; VC
Vi ; VC ; VL ; VR
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
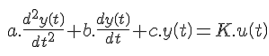
Sendo k=1, a=1, b=3 e c=2.
Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t) será:
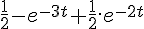
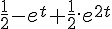
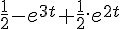
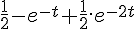
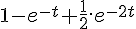
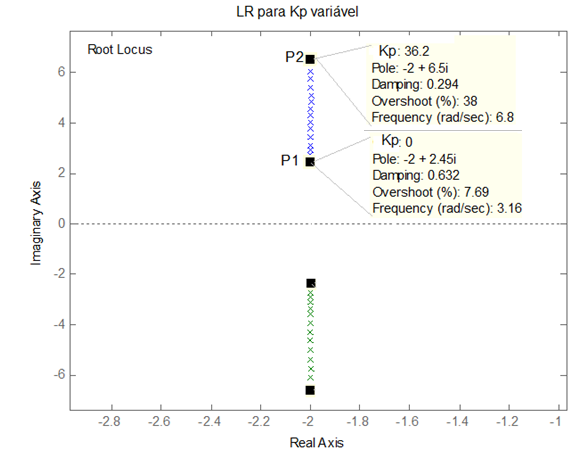
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.
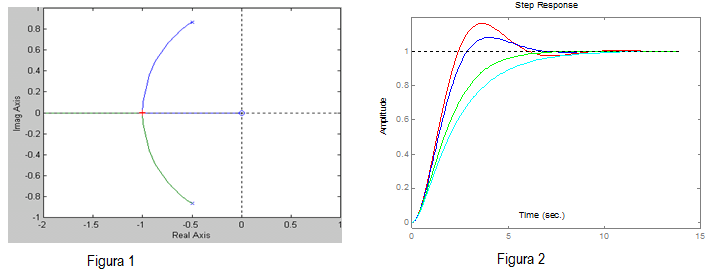
Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas:
Deseja-se controlar o sistema abaixo por malha fechada, dessa forma, qual será a variável manipulada (MV) e a variável controlada (PV).

PV : qi(t) e MV : h(t).
PV : qo(t) e MV : qi(t).
PV : h(t) e MV : qo(t).
PV : qi(t) e MV : qo(t).
PV : h(t) e MV : qi(t).
Nas equações apresentas abaixo, c(t) representa possíveis respostas de sistemas de segunda ordem, sujeitos a entrada do tipo degrau unitário.
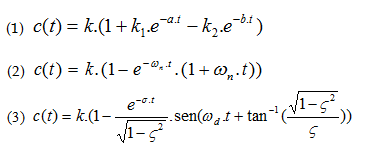
As equações (1), (2) e (3) correspondem, respectivamente, a respostas de sistemas:
Criticamente amortecido, sobreamortecido e subamortecido.
Criticamente amortecido, subamortecido e sobreamortecido.
Sobreamortecido, criticamente amortecido e subamortecido.
Subamortecido, sobreamortecido e criticamente amortecido.
Sobreamortecido, subamortecido e criticamente amortecido.
Considere o lugar das raízes de um sistema de controle com realimentação unitária, e controlador com ganho variável G dado na figura abaixo.

A partir da análise da informações contidas no gráfico, avalie a veracidade das afirmativas a seguir:
I - A equação caraterística do sistema é 1 + G. (s+1)/(s2 -3.s)=0
II - A Função de transferência de malha fechada do sistema de controle é: G(s+1)/(s2 + (G-3).s + G)
III - O lugar das raízes começa nos pólos s=0 e s=3, e terminos zeros s=-1 e s=-∞
IV - Dependendo do valor do parâmetro G, o sistema poderá ser estável ou instável
V - O sistema poderá responder de forma oscilatória ou monótona, dependendo do valor de G
São verdadeiras as afirmativas:
I, II, III, IV e V
II, III e V
II, III e IV
I, III, IV e V
II, III, IV e V
A figura abaixo apresenta o diagrama de um sistema de controle manual de um processo de aquecimento de água em um trocador de calor, usando vapor superaquecido como fonte de energia térmica.

Nos quadros numerados cabem os termos técnicos: processo, sistema de controle, sensor, controlador e atuador.
Nessa ordem, a numeração dos blocos será:
1 - processo; 2 - atuador ; 3 - sensor ; 4 - controlador ; 5 - sistema de controle
1 - processo; 2 - atuador ; 3 - sensor ; 4 - sistema de controle; 5 - controlador
1 - sistema de controle; 2 - processo; 3 - atuador ; 4 - sensor ; 5 - controlador
1 - processo; 2 - atuador ; 3 - sistema de controle; 4 - sensor; 5 - controlador
1 - processo; 2 - sistema de controle; 3 - atuador; 4 - sensor; 5 - controlador
Apresenta-se a seguir uma tabela com pares de transformadas de Laplace de algumas funções.
Porém, em uma mesma linha, pode ser que F(s) não seja a transformada de Laplace de f(t).
Na coluna A foi atribuída uma numeração das funções f(t).
Enumere a coluna B com o número da função f(t), de forma a haver a correta correspondência entre f(t) e F(s),
ou seja, que f(t) e F(s) correspondentes tenham a mesma numeração.

A coluna B, na forma transposta, terá a seguinte sequência numérica:
1 4 3 2 5 6 8 7 9
1 3 4 2 6 5 8 7 9
1 3 4 2 6 5 7 8 9
1 3 4 2 5 6 7 8 9
1 3 4 5 2 6 8 7 9
Na figura abaixo apresenta-se os diagramas elétrico e de blocos de um sistema físico.

As variáveis V1, V2, V3 e V4 correspondem, respectivamente às variáveis elétricas:
VC ; VR - VL ; I ; Vi
Vi ; VR ; VC ; VL
VL ; Vi - Vc ; I ; VC
Vi ; VR+VL ; I ; VC
Vi ; VC ; VL ; VR
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
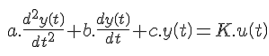
Sendo k=1, a=1, b=3 e c=2.
Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t) será:
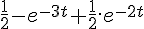
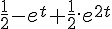
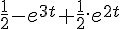
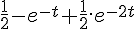
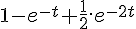
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.

Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas:
PV : qi(t) e MV : h(t).
PV : qo(t) e MV : qi(t).
PV : h(t) e MV : qo(t).
PV : qi(t) e MV : qo(t).
PV : h(t) e MV : qi(t).
Nas equações apresentas abaixo, c(t) representa possíveis respostas de sistemas de segunda ordem, sujeitos a entrada do tipo degrau unitário.
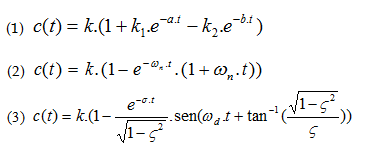
As equações (1), (2) e (3) correspondem, respectivamente, a respostas de sistemas:
Criticamente amortecido, sobreamortecido e subamortecido.
Criticamente amortecido, subamortecido e sobreamortecido.
Sobreamortecido, criticamente amortecido e subamortecido.
Subamortecido, sobreamortecido e criticamente amortecido.
Sobreamortecido, subamortecido e criticamente amortecido.
Considere o lugar das raízes de um sistema de controle com realimentação unitária, e controlador com ganho variável G dado na figura abaixo.

A partir da análise da informações contidas no gráfico, avalie a veracidade das afirmativas a seguir:
I - A equação caraterística do sistema é 1 + G. (s+1)/(s2 -3.s)=0
II - A Função de transferência de malha fechada do sistema de controle é: G(s+1)/(s2 + (G-3).s + G)
III - O lugar das raízes começa nos pólos s=0 e s=3, e terminos zeros s=-1 e s=-∞
IV - Dependendo do valor do parâmetro G, o sistema poderá ser estável ou instável
V - O sistema poderá responder de forma oscilatória ou monótona, dependendo do valor de G
São verdadeiras as afirmativas:
I, II, III, IV e V
II, III e V
II, III e IV
I, III, IV e V
II, III, IV e V
A figura abaixo apresenta o diagrama de um sistema de controle manual de um processo de aquecimento de água em um trocador de calor, usando vapor superaquecido como fonte de energia térmica.

Nos quadros numerados cabem os termos técnicos: processo, sistema de controle, sensor, controlador e atuador.
Nessa ordem, a numeração dos blocos será:
1 - processo; 2 - atuador ; 3 - sensor ; 4 - controlador ; 5 - sistema de controle
1 - processo; 2 - atuador ; 3 - sensor ; 4 - sistema de controle; 5 - controlador
1 - sistema de controle; 2 - processo; 3 - atuador ; 4 - sensor ; 5 - controlador
1 - processo; 2 - atuador ; 3 - sistema de controle; 4 - sensor; 5 - controlador
1 - processo; 2 - sistema de controle; 3 - atuador; 4 - sensor; 5 - controlador
Apresenta-se a seguir uma tabela com pares de transformadas de Laplace de algumas funções.
Porém, em uma mesma linha, pode ser que F(s) não seja a transformada de Laplace de f(t).
Na coluna A foi atribuída uma numeração das funções f(t).
Enumere a coluna B com o número da função f(t), de forma a haver a correta correspondência entre f(t) e F(s),
ou seja, que f(t) e F(s) correspondentes tenham a mesma numeração.

A coluna B, na forma transposta, terá a seguinte sequência numérica:
1 4 3 2 5 6 8 7 9
1 3 4 2 6 5 8 7 9
1 3 4 2 6 5 7 8 9
1 3 4 2 5 6 7 8 9
1 3 4 5 2 6 8 7 9
Na figura abaixo apresenta-se os diagramas elétrico e de blocos de um sistema físico.

As variáveis V1, V2, V3 e V4 correspondem, respectivamente às variáveis elétricas:
VC ; VR - VL ; I ; Vi
Vi ; VR ; VC ; VL
VL ; Vi - Vc ; I ; VC
Vi ; VR+VL ; I ; VC
Vi ; VC ; VL ; VR
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
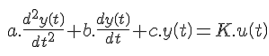
Sendo k=1, a=1, b=3 e c=2.
Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t) será:
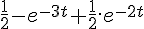
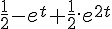
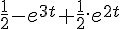
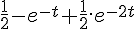
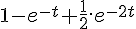
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.

Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas:
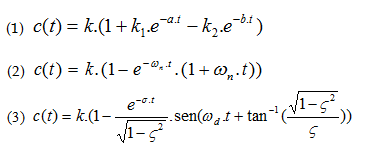
Criticamente amortecido, sobreamortecido e subamortecido.
Criticamente amortecido, subamortecido e sobreamortecido.
Sobreamortecido, criticamente amortecido e subamortecido.
Subamortecido, sobreamortecido e criticamente amortecido.
Sobreamortecido, subamortecido e criticamente amortecido.
Considere o lugar das raízes de um sistema de controle com realimentação unitária, e controlador com ganho variável G dado na figura abaixo.

A partir da análise da informações contidas no gráfico, avalie a veracidade das afirmativas a seguir:
I - A equação caraterística do sistema é 1 + G. (s+1)/(s2 -3.s)=0
II - A Função de transferência de malha fechada do sistema de controle é: G(s+1)/(s2 + (G-3).s + G)
III - O lugar das raízes começa nos pólos s=0 e s=3, e terminos zeros s=-1 e s=-∞
IV - Dependendo do valor do parâmetro G, o sistema poderá ser estável ou instável
V - O sistema poderá responder de forma oscilatória ou monótona, dependendo do valor de G
São verdadeiras as afirmativas:
I, II, III, IV e V
II, III e V
II, III e IV
I, III, IV e V
II, III, IV e V
A figura abaixo apresenta o diagrama de um sistema de controle manual de um processo de aquecimento de água em um trocador de calor, usando vapor superaquecido como fonte de energia térmica.

Nos quadros numerados cabem os termos técnicos: processo, sistema de controle, sensor, controlador e atuador.
Nessa ordem, a numeração dos blocos será:
1 - processo; 2 - atuador ; 3 - sensor ; 4 - controlador ; 5 - sistema de controle
1 - processo; 2 - atuador ; 3 - sensor ; 4 - sistema de controle; 5 - controlador
1 - sistema de controle; 2 - processo; 3 - atuador ; 4 - sensor ; 5 - controlador
1 - processo; 2 - atuador ; 3 - sistema de controle; 4 - sensor; 5 - controlador
1 - processo; 2 - sistema de controle; 3 - atuador; 4 - sensor; 5 - controlador
Apresenta-se a seguir uma tabela com pares de transformadas de Laplace de algumas funções.
Porém, em uma mesma linha, pode ser que F(s) não seja a transformada de Laplace de f(t).
Na coluna A foi atribuída uma numeração das funções f(t).
Enumere a coluna B com o número da função f(t), de forma a haver a correta correspondência entre f(t) e F(s),
ou seja, que f(t) e F(s) correspondentes tenham a mesma numeração.

A coluna B, na forma transposta, terá a seguinte sequência numérica:
1 4 3 2 5 6 8 7 9
1 3 4 2 6 5 8 7 9
1 3 4 2 6 5 7 8 9
1 3 4 2 5 6 7 8 9
1 3 4 5 2 6 8 7 9
Na figura abaixo apresenta-se os diagramas elétrico e de blocos de um sistema físico.

As variáveis V1, V2, V3 e V4 correspondem, respectivamente às variáveis elétricas:
VC ; VR - VL ; I ; Vi
Vi ; VR ; VC ; VL
VL ; Vi - Vc ; I ; VC
Vi ; VR+VL ; I ; VC
Vi ; VC ; VL ; VR
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
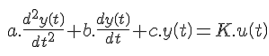
Sendo k=1, a=1, b=3 e c=2.
Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t) será:
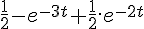
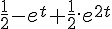
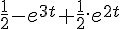
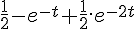
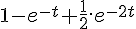
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.

Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas:

I, II, III, IV e V
II, III e V
II, III e IV
I, III, IV e V
II, III, IV e V
A figura abaixo apresenta o diagrama de um sistema de controle manual de um processo de aquecimento de água em um trocador de calor, usando vapor superaquecido como fonte de energia térmica.

Nos quadros numerados cabem os termos técnicos: processo, sistema de controle, sensor, controlador e atuador.
Nessa ordem, a numeração dos blocos será:
1 - processo; 2 - atuador ; 3 - sensor ; 4 - controlador ; 5 - sistema de controle
1 - processo; 2 - atuador ; 3 - sensor ; 4 - sistema de controle; 5 - controlador
1 - sistema de controle; 2 - processo; 3 - atuador ; 4 - sensor ; 5 - controlador
1 - processo; 2 - atuador ; 3 - sistema de controle; 4 - sensor; 5 - controlador
1 - processo; 2 - sistema de controle; 3 - atuador; 4 - sensor; 5 - controlador
Apresenta-se a seguir uma tabela com pares de transformadas de Laplace de algumas funções.
Porém, em uma mesma linha, pode ser que F(s) não seja a transformada de Laplace de f(t).
Na coluna A foi atribuída uma numeração das funções f(t).
Enumere a coluna B com o número da função f(t), de forma a haver a correta correspondência entre f(t) e F(s),
ou seja, que f(t) e F(s) correspondentes tenham a mesma numeração.

A coluna B, na forma transposta, terá a seguinte sequência numérica:
1 4 3 2 5 6 8 7 9
1 3 4 2 6 5 8 7 9
1 3 4 2 6 5 7 8 9
1 3 4 2 5 6 7 8 9
1 3 4 5 2 6 8 7 9
Na figura abaixo apresenta-se os diagramas elétrico e de blocos de um sistema físico.

As variáveis V1, V2, V3 e V4 correspondem, respectivamente às variáveis elétricas:
VC ; VR - VL ; I ; Vi
Vi ; VR ; VC ; VL
VL ; Vi - Vc ; I ; VC
Vi ; VR+VL ; I ; VC
Vi ; VC ; VL ; VR
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
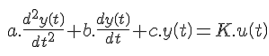
Sendo k=1, a=1, b=3 e c=2.
Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t) será:
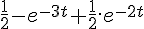
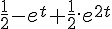
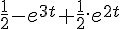
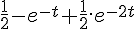
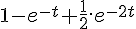
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.

Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas:

1 - processo; 2 - atuador ; 3 - sensor ; 4 - controlador ; 5 - sistema de controle
1 - processo; 2 - atuador ; 3 - sensor ; 4 - sistema de controle; 5 - controlador
1 - sistema de controle; 2 - processo; 3 - atuador ; 4 - sensor ; 5 - controlador
1 - processo; 2 - atuador ; 3 - sistema de controle; 4 - sensor; 5 - controlador
1 - processo; 2 - sistema de controle; 3 - atuador; 4 - sensor; 5 - controlador
Apresenta-se a seguir uma tabela com pares de transformadas de Laplace de algumas funções.
Porém, em uma mesma linha, pode ser que F(s) não seja a transformada de Laplace de f(t).
Na coluna A foi atribuída uma numeração das funções f(t).
Enumere a coluna B com o número da função f(t), de forma a haver a correta correspondência entre f(t) e F(s),
ou seja, que f(t) e F(s) correspondentes tenham a mesma numeração.

A coluna B, na forma transposta, terá a seguinte sequência numérica:
1 4 3 2 5 6 8 7 9
1 3 4 2 6 5 8 7 9
1 3 4 2 6 5 7 8 9
1 3 4 2 5 6 7 8 9
1 3 4 5 2 6 8 7 9
Na figura abaixo apresenta-se os diagramas elétrico e de blocos de um sistema físico.

As variáveis V1, V2, V3 e V4 correspondem, respectivamente às variáveis elétricas:
VC ; VR - VL ; I ; Vi
Vi ; VR ; VC ; VL
VL ; Vi - Vc ; I ; VC
Vi ; VR+VL ; I ; VC
Vi ; VC ; VL ; VR
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
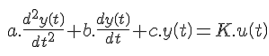
Sendo k=1, a=1, b=3 e c=2.
Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t) será:
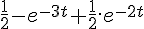
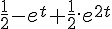
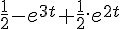
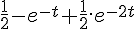
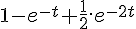
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.

Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas:

1 4 3 2 5 6 8 7 9
1 3 4 2 6 5 8 7 9
1 3 4 2 6 5 7 8 9
1 3 4 2 5 6 7 8 9
1 3 4 5 2 6 8 7 9
Na figura abaixo apresenta-se os diagramas elétrico e de blocos de um sistema físico.

As variáveis V1, V2, V3 e V4 correspondem, respectivamente às variáveis elétricas:
VC ; VR - VL ; I ; Vi
Vi ; VR ; VC ; VL
VL ; Vi - Vc ; I ; VC
Vi ; VR+VL ; I ; VC
Vi ; VC ; VL ; VR
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
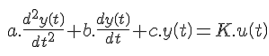
Sendo k=1, a=1, b=3 e c=2.
Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t) será:
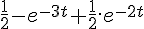
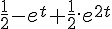
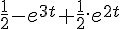
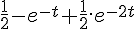
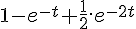
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.

Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas:

VC ; VR - VL ; I ; Vi
Vi ; VR ; VC ; VL
VL ; Vi - Vc ; I ; VC
Vi ; VR+VL ; I ; VC
Vi ; VC ; VL ; VR
Um sistema de controle de posição de braço de robô tem como variável de entrada tensão u(t), dada em volts, e pode ter duas variáveis de saída: velocidade v(t) dada em metros por segundo, e o deslocamento y(t) dado em metros.
O comportamento dinâmico do sistema é dado pela equação diferencial:
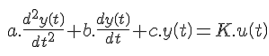
Sendo k=1, a=1, b=3 e c=2.
Considerando o sinal de excitação u(t) do tipo degrau unitário, a resposta y(t) será:
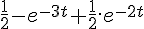
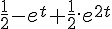
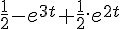
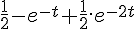
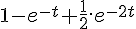
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.

Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas:
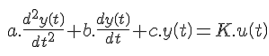
Nas figuras a seguir são apresentados respectivamente o gráfico do lugar das raízes de um sistema de controle, e respostas desse mesmo sistema para entrada degrau unitário, para 4 valores distintos do parâmetro ajustável K do controlador.

Considerando que o sistema tem realimentação unitária, e que o controlador é do tipo proporcional, avalie a veracidade das afirmativas a seguir:
I - Nas respostas oscilatórias foram utilizados valores de K maiores que nas repostas exponenciais
II - O menor valor de K foi utilizado na reposta de maior overshoot
III - O valor de K aumenta da curva de maior para a de menor overshoot
IV - O maior valor de K foi utilizado na curva de maior tempo de acomodação;
V - As respostas exponenciais (não-oscilatórias) foram utilizados valores de K que tornam os pólos do sistema reais.
São corretas as afirmativas: