CONTEÚDOS E METODOLOGIAS DO ENSINO DE MATEMÁTICA
Ao dividirmos em partes iguais uma grandeza, considerada como um todo, cada uma das partes é uma unidade fracionária. Uma ou mais unidades fracionárias reunidas constituem uma fração.
Com base nesta afirmação analise cada desenho e assinale a alternativa que indica a representação de uma fração.
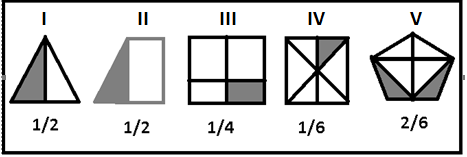
Ilustração V
Ilustração IV
Ilustraçao I
Ilustração III
Ilustração II

O mínimo múltiplo comum de dois números naturais a e b é o menor dos seus múltiplos comuns.
Em uma competição de ciclismo, o atleta A levou 180 minutos (3h) para realizar o circuito completo, os ciclistas B e C levaram 210 (3h 30) e 220 minutos (3h 40) respectivamente para realizar o mesmo circuito. Suponha que, num dado momento, os três atletas passem juntos, pelo mesmo ponto do circuito. Após quantos minutos eles voltarão a se alinhar, e passar por esse ponto?
É correto APENAS o que se afirma em:
13.900 minutos (23 h).
13.800 minutos (230h).
610 minutos (10h).
270 minutos (4h 30).
13.860 minutos (231h).

Calcule o MDC e o MMC dos números pensados por Ana e por Luísa e verifique quem é a mais velha e quem alcançou a média, total, mais alta.
É correto APENAS o que se afirma em´:
Luísa é a mais velha e ambas obtiveram a mesma média.
Ana é a mais velha e também obteve média maior.
Luísa é a mais velha e também obteve média maior.
Luísa é a mais velha e Ana obteve média maior.
Ana é a mais velha e Luísa obteve média maior.
O sistema de numeração utilizado atualmente, na maioria de nossas culturas contemporâneas, é denominado sistema indo-arábico. Trata-se de um sistema decimal, daí porque usualmente nos referimos a ele chamando-o de sistema de numeração decimal. A palavra decimal tem sua origem na palavra “decem”, que significa dez, pois, assim como vários sistemas de numeração antigos, o nosso atual sistema também é de base dez, ou seja, os agrupamentos são sempre feitos de dez em dez. (CENTURIÓN, Marília. Números e operações. p.32,1995.)
Sobre o sistema de numeração decimal assinale a alternativa errada.
No sistema de numeração decimal o algarismo tem valor posicional, o que significa que ele tem um valor absoluto; o valor do algarismo depende da posição que ele ocupa no número. E o valor relativo, que é o valor do próprio algarismo.
No sistema de numeração decimal, cada algarismo escrito imediatamente à esquerda de outro tem um valor dez vezes maior que teria se tivesse na posição do outro.
O conjunto dos números naturais servem para contar coisas, podemos sempre supor algo a “mais” a ser contado, para isso precisamos de um novo número, o seguinte na sucessão dos números naturais. Mediante está afirmação, todo número natural tem um sucessor, e consequentemente um antecessor, exceto o zero.
O sistema de numeração decimal é multiplicativo, visto que o valor do algarismo é multiplicado pelo valor da casa ocupada.
O ensino do sistema de numeração decimal deve considerar a exploração e/ou manipulação de diferentes recursos pedagógicos; a articulação dos princípios do sistema de numeração com as regras das operações matemáticas e o trabalho com diferentes bases.
– A abordagem dos números racionais no segundo ciclo tem como objetivo principal levar os alunos a perceberem que os números naturais, já conhecidos, são insuficientes para resolver.(PCN de Matemática, pagina 63.)
Assim, identificar, encontrar estratégias de resolução de operações com números fracionários passa a ser parte integrante do cotidiano do aluno.
Sobre como resolver operações envolvendo frações assinale a afirmativa errada.
Na multiplicação de frações multiplicarmos, numerador por numerador e denominador por denominador, respeitando suas posições.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos.
A divisão deve ser efetuada aplicando uma regra prática e de fácil assimilação, que diz: “repetir a primeira fração e multiplicar pelo inverso da segunda”.
Nas operações da adição ou subtração envolvendo números na forma de fração com numeradores diferentes, devemos criar um novo numerador através do cálculo do mínimo múltiplo comum – MMC dos numeradores fornecidos.
Quando os denominadores das frações forem guais, os numeradores serão somados ou subtraídos, de acordo com os sinais operatórios, e o valor do denominador será mantido.
As crianças desde muito cedo, dividem, repartem, distribuem coisas. Essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida e a de repartir em partes iguais. A ideia é de medida quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados. A ideia da divisão é de repartir quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir.
- Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
- Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
- Ari comprou 48 figurinhas e vai dividir essas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
- Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
Assinale a sequência correta.
R, M, R, R, M
M, M, R. R. M
R, R, R, M, M
M, R, R, M, M
M, R, M, R, M
No dia-a-dia as pessoas e as crianças em particular, dividem, repartem, distribuem coisas. essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida (M) e a de repartir (R) em partes iguais.
A ideia da divisão é de repartir (R) quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
A ideia é de medida (M) quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir. Em seguida assinale a sequência correta.
I – Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
II – Ari comprou 48 figurinhas e vai dividir estas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
III- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
IV – Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
V - Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
R, R, R, R, R
R, R, M, M, R
M, M, M, M, M
R, R, M, M, M
M, M, R, R, R
As crianças desde muito cedo realizam contagens e relacionam pequenas quantidades a essa contagem. Elas contam no dedo, contam com palitos dentre outros objetos. Para sistematizar o processo de contagem, estabelecer a relação número quantidade e compreender o sistema de numeração, o professor pode utilizar o material Dourado.
“Material Dourado é um dos materiais idealizados pela médica e educadora Maria Montessori. Ele tem como foco o trabalho com a matemática. Apesar de ter sido elaborado para o trabalho com aritmética, seguiu os mesmos princípios montessorianos sobre a educação sensorial”. Disponível em: http://pt.wikipedia.org/wiki/Material_Dourado. Acesso em: 07/02/2017.
Leia e analise as alternativas abaixo, em seguida assinale a alternativa que não corresponde a característica ou aplicabilidade desse recurso na sala de aula.
O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?


Ilustração V
Ilustração IV
Ilustraçao I
Ilustração III
Ilustração II

O mínimo múltiplo comum de dois números naturais a e b é o menor dos seus múltiplos comuns.
Em uma competição de ciclismo, o atleta A levou 180 minutos (3h) para realizar o circuito completo, os ciclistas B e C levaram 210 (3h 30) e 220 minutos (3h 40) respectivamente para realizar o mesmo circuito. Suponha que, num dado momento, os três atletas passem juntos, pelo mesmo ponto do circuito. Após quantos minutos eles voltarão a se alinhar, e passar por esse ponto?
É correto APENAS o que se afirma em:
13.900 minutos (23 h).
13.800 minutos (230h).
610 minutos (10h).
270 minutos (4h 30).
13.860 minutos (231h).

Calcule o MDC e o MMC dos números pensados por Ana e por Luísa e verifique quem é a mais velha e quem alcançou a média, total, mais alta.
É correto APENAS o que se afirma em´:
Luísa é a mais velha e ambas obtiveram a mesma média.
Ana é a mais velha e também obteve média maior.
Luísa é a mais velha e também obteve média maior.
Luísa é a mais velha e Ana obteve média maior.
Ana é a mais velha e Luísa obteve média maior.
O sistema de numeração utilizado atualmente, na maioria de nossas culturas contemporâneas, é denominado sistema indo-arábico. Trata-se de um sistema decimal, daí porque usualmente nos referimos a ele chamando-o de sistema de numeração decimal. A palavra decimal tem sua origem na palavra “decem”, que significa dez, pois, assim como vários sistemas de numeração antigos, o nosso atual sistema também é de base dez, ou seja, os agrupamentos são sempre feitos de dez em dez. (CENTURIÓN, Marília. Números e operações. p.32,1995.)
Sobre o sistema de numeração decimal assinale a alternativa errada.
No sistema de numeração decimal o algarismo tem valor posicional, o que significa que ele tem um valor absoluto; o valor do algarismo depende da posição que ele ocupa no número. E o valor relativo, que é o valor do próprio algarismo.
No sistema de numeração decimal, cada algarismo escrito imediatamente à esquerda de outro tem um valor dez vezes maior que teria se tivesse na posição do outro.
O conjunto dos números naturais servem para contar coisas, podemos sempre supor algo a “mais” a ser contado, para isso precisamos de um novo número, o seguinte na sucessão dos números naturais. Mediante está afirmação, todo número natural tem um sucessor, e consequentemente um antecessor, exceto o zero.
O sistema de numeração decimal é multiplicativo, visto que o valor do algarismo é multiplicado pelo valor da casa ocupada.
O ensino do sistema de numeração decimal deve considerar a exploração e/ou manipulação de diferentes recursos pedagógicos; a articulação dos princípios do sistema de numeração com as regras das operações matemáticas e o trabalho com diferentes bases.
– A abordagem dos números racionais no segundo ciclo tem como objetivo principal levar os alunos a perceberem que os números naturais, já conhecidos, são insuficientes para resolver.(PCN de Matemática, pagina 63.)
Assim, identificar, encontrar estratégias de resolução de operações com números fracionários passa a ser parte integrante do cotidiano do aluno.
Sobre como resolver operações envolvendo frações assinale a afirmativa errada.
Na multiplicação de frações multiplicarmos, numerador por numerador e denominador por denominador, respeitando suas posições.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos.
A divisão deve ser efetuada aplicando uma regra prática e de fácil assimilação, que diz: “repetir a primeira fração e multiplicar pelo inverso da segunda”.
Nas operações da adição ou subtração envolvendo números na forma de fração com numeradores diferentes, devemos criar um novo numerador através do cálculo do mínimo múltiplo comum – MMC dos numeradores fornecidos.
Quando os denominadores das frações forem guais, os numeradores serão somados ou subtraídos, de acordo com os sinais operatórios, e o valor do denominador será mantido.
As crianças desde muito cedo, dividem, repartem, distribuem coisas. Essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida e a de repartir em partes iguais. A ideia é de medida quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados. A ideia da divisão é de repartir quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir.
- Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
- Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
- Ari comprou 48 figurinhas e vai dividir essas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
- Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
Assinale a sequência correta.
R, M, R, R, M
M, M, R. R. M
R, R, R, M, M
M, R, R, M, M
M, R, M, R, M
No dia-a-dia as pessoas e as crianças em particular, dividem, repartem, distribuem coisas. essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida (M) e a de repartir (R) em partes iguais.
A ideia da divisão é de repartir (R) quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
A ideia é de medida (M) quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir. Em seguida assinale a sequência correta.
I – Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
II – Ari comprou 48 figurinhas e vai dividir estas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
III- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
IV – Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
V - Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
R, R, R, R, R
R, R, M, M, R
M, M, M, M, M
R, R, M, M, M
M, M, R, R, R
As crianças desde muito cedo realizam contagens e relacionam pequenas quantidades a essa contagem. Elas contam no dedo, contam com palitos dentre outros objetos. Para sistematizar o processo de contagem, estabelecer a relação número quantidade e compreender o sistema de numeração, o professor pode utilizar o material Dourado.
“Material Dourado é um dos materiais idealizados pela médica e educadora Maria Montessori. Ele tem como foco o trabalho com a matemática. Apesar de ter sido elaborado para o trabalho com aritmética, seguiu os mesmos princípios montessorianos sobre a educação sensorial”. Disponível em: http://pt.wikipedia.org/wiki/Material_Dourado. Acesso em: 07/02/2017.
Leia e analise as alternativas abaixo, em seguida assinale a alternativa que não corresponde a característica ou aplicabilidade desse recurso na sala de aula.
O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?

13.900 minutos (23 h).
13.800 minutos (230h).
610 minutos (10h).
270 minutos (4h 30).
13.860 minutos (231h).

Calcule o MDC e o MMC dos números pensados por Ana e por Luísa e verifique quem é a mais velha e quem alcançou a média, total, mais alta.
É correto APENAS o que se afirma em´:
Luísa é a mais velha e ambas obtiveram a mesma média.
Ana é a mais velha e também obteve média maior.
Luísa é a mais velha e também obteve média maior.
Luísa é a mais velha e Ana obteve média maior.
Ana é a mais velha e Luísa obteve média maior.
O sistema de numeração utilizado atualmente, na maioria de nossas culturas contemporâneas, é denominado sistema indo-arábico. Trata-se de um sistema decimal, daí porque usualmente nos referimos a ele chamando-o de sistema de numeração decimal. A palavra decimal tem sua origem na palavra “decem”, que significa dez, pois, assim como vários sistemas de numeração antigos, o nosso atual sistema também é de base dez, ou seja, os agrupamentos são sempre feitos de dez em dez. (CENTURIÓN, Marília. Números e operações. p.32,1995.)
Sobre o sistema de numeração decimal assinale a alternativa errada.
No sistema de numeração decimal o algarismo tem valor posicional, o que significa que ele tem um valor absoluto; o valor do algarismo depende da posição que ele ocupa no número. E o valor relativo, que é o valor do próprio algarismo.
No sistema de numeração decimal, cada algarismo escrito imediatamente à esquerda de outro tem um valor dez vezes maior que teria se tivesse na posição do outro.
O conjunto dos números naturais servem para contar coisas, podemos sempre supor algo a “mais” a ser contado, para isso precisamos de um novo número, o seguinte na sucessão dos números naturais. Mediante está afirmação, todo número natural tem um sucessor, e consequentemente um antecessor, exceto o zero.
O sistema de numeração decimal é multiplicativo, visto que o valor do algarismo é multiplicado pelo valor da casa ocupada.
O ensino do sistema de numeração decimal deve considerar a exploração e/ou manipulação de diferentes recursos pedagógicos; a articulação dos princípios do sistema de numeração com as regras das operações matemáticas e o trabalho com diferentes bases.
– A abordagem dos números racionais no segundo ciclo tem como objetivo principal levar os alunos a perceberem que os números naturais, já conhecidos, são insuficientes para resolver.(PCN de Matemática, pagina 63.)
Assim, identificar, encontrar estratégias de resolução de operações com números fracionários passa a ser parte integrante do cotidiano do aluno.
Sobre como resolver operações envolvendo frações assinale a afirmativa errada.
Na multiplicação de frações multiplicarmos, numerador por numerador e denominador por denominador, respeitando suas posições.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos.
A divisão deve ser efetuada aplicando uma regra prática e de fácil assimilação, que diz: “repetir a primeira fração e multiplicar pelo inverso da segunda”.
Nas operações da adição ou subtração envolvendo números na forma de fração com numeradores diferentes, devemos criar um novo numerador através do cálculo do mínimo múltiplo comum – MMC dos numeradores fornecidos.
Quando os denominadores das frações forem guais, os numeradores serão somados ou subtraídos, de acordo com os sinais operatórios, e o valor do denominador será mantido.
As crianças desde muito cedo, dividem, repartem, distribuem coisas. Essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida e a de repartir em partes iguais. A ideia é de medida quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados. A ideia da divisão é de repartir quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir.
- Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
- Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
- Ari comprou 48 figurinhas e vai dividir essas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
- Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
Assinale a sequência correta.
R, M, R, R, M
M, M, R. R. M
R, R, R, M, M
M, R, R, M, M
M, R, M, R, M
No dia-a-dia as pessoas e as crianças em particular, dividem, repartem, distribuem coisas. essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida (M) e a de repartir (R) em partes iguais.
A ideia da divisão é de repartir (R) quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
A ideia é de medida (M) quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir. Em seguida assinale a sequência correta.
I – Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
II – Ari comprou 48 figurinhas e vai dividir estas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
III- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
IV – Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
V - Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
R, R, R, R, R
R, R, M, M, R
M, M, M, M, M
R, R, M, M, M
M, M, R, R, R
As crianças desde muito cedo realizam contagens e relacionam pequenas quantidades a essa contagem. Elas contam no dedo, contam com palitos dentre outros objetos. Para sistematizar o processo de contagem, estabelecer a relação número quantidade e compreender o sistema de numeração, o professor pode utilizar o material Dourado.
“Material Dourado é um dos materiais idealizados pela médica e educadora Maria Montessori. Ele tem como foco o trabalho com a matemática. Apesar de ter sido elaborado para o trabalho com aritmética, seguiu os mesmos princípios montessorianos sobre a educação sensorial”. Disponível em: http://pt.wikipedia.org/wiki/Material_Dourado. Acesso em: 07/02/2017.
Leia e analise as alternativas abaixo, em seguida assinale a alternativa que não corresponde a característica ou aplicabilidade desse recurso na sala de aula.
O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?

Luísa é a mais velha e ambas obtiveram a mesma média.
Ana é a mais velha e também obteve média maior.
Luísa é a mais velha e também obteve média maior.
Luísa é a mais velha e Ana obteve média maior.
Ana é a mais velha e Luísa obteve média maior.
O sistema de numeração utilizado atualmente, na maioria de nossas culturas contemporâneas, é denominado sistema indo-arábico. Trata-se de um sistema decimal, daí porque usualmente nos referimos a ele chamando-o de sistema de numeração decimal. A palavra decimal tem sua origem na palavra “decem”, que significa dez, pois, assim como vários sistemas de numeração antigos, o nosso atual sistema também é de base dez, ou seja, os agrupamentos são sempre feitos de dez em dez. (CENTURIÓN, Marília. Números e operações. p.32,1995.)
Sobre o sistema de numeração decimal assinale a alternativa errada.
No sistema de numeração decimal o algarismo tem valor posicional, o que significa que ele tem um valor absoluto; o valor do algarismo depende da posição que ele ocupa no número. E o valor relativo, que é o valor do próprio algarismo.
No sistema de numeração decimal, cada algarismo escrito imediatamente à esquerda de outro tem um valor dez vezes maior que teria se tivesse na posição do outro.
O conjunto dos números naturais servem para contar coisas, podemos sempre supor algo a “mais” a ser contado, para isso precisamos de um novo número, o seguinte na sucessão dos números naturais. Mediante está afirmação, todo número natural tem um sucessor, e consequentemente um antecessor, exceto o zero.
O sistema de numeração decimal é multiplicativo, visto que o valor do algarismo é multiplicado pelo valor da casa ocupada.
O ensino do sistema de numeração decimal deve considerar a exploração e/ou manipulação de diferentes recursos pedagógicos; a articulação dos princípios do sistema de numeração com as regras das operações matemáticas e o trabalho com diferentes bases.
– A abordagem dos números racionais no segundo ciclo tem como objetivo principal levar os alunos a perceberem que os números naturais, já conhecidos, são insuficientes para resolver.(PCN de Matemática, pagina 63.)
Assim, identificar, encontrar estratégias de resolução de operações com números fracionários passa a ser parte integrante do cotidiano do aluno.
Sobre como resolver operações envolvendo frações assinale a afirmativa errada.
Na multiplicação de frações multiplicarmos, numerador por numerador e denominador por denominador, respeitando suas posições.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos.
A divisão deve ser efetuada aplicando uma regra prática e de fácil assimilação, que diz: “repetir a primeira fração e multiplicar pelo inverso da segunda”.
Nas operações da adição ou subtração envolvendo números na forma de fração com numeradores diferentes, devemos criar um novo numerador através do cálculo do mínimo múltiplo comum – MMC dos numeradores fornecidos.
Quando os denominadores das frações forem guais, os numeradores serão somados ou subtraídos, de acordo com os sinais operatórios, e o valor do denominador será mantido.
As crianças desde muito cedo, dividem, repartem, distribuem coisas. Essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida e a de repartir em partes iguais. A ideia é de medida quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados. A ideia da divisão é de repartir quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir.
- Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
- Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
- Ari comprou 48 figurinhas e vai dividir essas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
- Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
Assinale a sequência correta.
R, M, R, R, M
M, M, R. R. M
R, R, R, M, M
M, R, R, M, M
M, R, M, R, M
No dia-a-dia as pessoas e as crianças em particular, dividem, repartem, distribuem coisas. essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida (M) e a de repartir (R) em partes iguais.
A ideia da divisão é de repartir (R) quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
A ideia é de medida (M) quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir. Em seguida assinale a sequência correta.
I – Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
II – Ari comprou 48 figurinhas e vai dividir estas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
III- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
IV – Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
V - Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
R, R, R, R, R
R, R, M, M, R
M, M, M, M, M
R, R, M, M, M
M, M, R, R, R
As crianças desde muito cedo realizam contagens e relacionam pequenas quantidades a essa contagem. Elas contam no dedo, contam com palitos dentre outros objetos. Para sistematizar o processo de contagem, estabelecer a relação número quantidade e compreender o sistema de numeração, o professor pode utilizar o material Dourado.
“Material Dourado é um dos materiais idealizados pela médica e educadora Maria Montessori. Ele tem como foco o trabalho com a matemática. Apesar de ter sido elaborado para o trabalho com aritmética, seguiu os mesmos princípios montessorianos sobre a educação sensorial”. Disponível em: http://pt.wikipedia.org/wiki/Material_Dourado. Acesso em: 07/02/2017.
Leia e analise as alternativas abaixo, em seguida assinale a alternativa que não corresponde a característica ou aplicabilidade desse recurso na sala de aula.
O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?

No sistema de numeração decimal o algarismo tem valor posicional, o que significa que ele tem um valor absoluto; o valor do algarismo depende da posição que ele ocupa no número. E o valor relativo, que é o valor do próprio algarismo.
No sistema de numeração decimal, cada algarismo escrito imediatamente à esquerda de outro tem um valor dez vezes maior que teria se tivesse na posição do outro.
O conjunto dos números naturais servem para contar coisas, podemos sempre supor algo a “mais” a ser contado, para isso precisamos de um novo número, o seguinte na sucessão dos números naturais. Mediante está afirmação, todo número natural tem um sucessor, e consequentemente um antecessor, exceto o zero.
O sistema de numeração decimal é multiplicativo, visto que o valor do algarismo é multiplicado pelo valor da casa ocupada.
O ensino do sistema de numeração decimal deve considerar a exploração e/ou manipulação de diferentes recursos pedagógicos; a articulação dos princípios do sistema de numeração com as regras das operações matemáticas e o trabalho com diferentes bases.
– A abordagem dos números racionais no segundo ciclo tem como objetivo principal levar os alunos a perceberem que os números naturais, já conhecidos, são insuficientes para resolver.(PCN de Matemática, pagina 63.)
Assim, identificar, encontrar estratégias de resolução de operações com números fracionários passa a ser parte integrante do cotidiano do aluno.
Sobre como resolver operações envolvendo frações assinale a afirmativa errada.
Na multiplicação de frações multiplicarmos, numerador por numerador e denominador por denominador, respeitando suas posições.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos.
A divisão deve ser efetuada aplicando uma regra prática e de fácil assimilação, que diz: “repetir a primeira fração e multiplicar pelo inverso da segunda”.
Nas operações da adição ou subtração envolvendo números na forma de fração com numeradores diferentes, devemos criar um novo numerador através do cálculo do mínimo múltiplo comum – MMC dos numeradores fornecidos.
Quando os denominadores das frações forem guais, os numeradores serão somados ou subtraídos, de acordo com os sinais operatórios, e o valor do denominador será mantido.
As crianças desde muito cedo, dividem, repartem, distribuem coisas. Essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida e a de repartir em partes iguais. A ideia é de medida quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados. A ideia da divisão é de repartir quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir.
- Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
- Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
- Ari comprou 48 figurinhas e vai dividir essas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
- Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
Assinale a sequência correta.
R, M, R, R, M
M, M, R. R. M
R, R, R, M, M
M, R, R, M, M
M, R, M, R, M
No dia-a-dia as pessoas e as crianças em particular, dividem, repartem, distribuem coisas. essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida (M) e a de repartir (R) em partes iguais.
A ideia da divisão é de repartir (R) quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
A ideia é de medida (M) quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir. Em seguida assinale a sequência correta.
I – Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
II – Ari comprou 48 figurinhas e vai dividir estas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
III- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
IV – Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
V - Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
R, R, R, R, R
R, R, M, M, R
M, M, M, M, M
R, R, M, M, M
M, M, R, R, R
As crianças desde muito cedo realizam contagens e relacionam pequenas quantidades a essa contagem. Elas contam no dedo, contam com palitos dentre outros objetos. Para sistematizar o processo de contagem, estabelecer a relação número quantidade e compreender o sistema de numeração, o professor pode utilizar o material Dourado.
“Material Dourado é um dos materiais idealizados pela médica e educadora Maria Montessori. Ele tem como foco o trabalho com a matemática. Apesar de ter sido elaborado para o trabalho com aritmética, seguiu os mesmos princípios montessorianos sobre a educação sensorial”. Disponível em: http://pt.wikipedia.org/wiki/Material_Dourado. Acesso em: 07/02/2017.
Leia e analise as alternativas abaixo, em seguida assinale a alternativa que não corresponde a característica ou aplicabilidade desse recurso na sala de aula.
O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?

Na multiplicação de frações multiplicarmos, numerador por numerador e denominador por denominador, respeitando suas posições.
Nas operações da adição ou subtração envolvendo números na forma de fração com denominadores diferentes, devemos criar um novo denominador através do cálculo do mínimo múltiplo comum – MMC dos denominadores fornecidos.
A divisão deve ser efetuada aplicando uma regra prática e de fácil assimilação, que diz: “repetir a primeira fração e multiplicar pelo inverso da segunda”.
Nas operações da adição ou subtração envolvendo números na forma de fração com numeradores diferentes, devemos criar um novo numerador através do cálculo do mínimo múltiplo comum – MMC dos numeradores fornecidos.
Quando os denominadores das frações forem guais, os numeradores serão somados ou subtraídos, de acordo com os sinais operatórios, e o valor do denominador será mantido.
As crianças desde muito cedo, dividem, repartem, distribuem coisas. Essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida e a de repartir em partes iguais. A ideia é de medida quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados. A ideia da divisão é de repartir quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir.
- Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
- Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
- Ari comprou 48 figurinhas e vai dividir essas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
- Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
Assinale a sequência correta.
R, M, R, R, M
M, M, R. R. M
R, R, R, M, M
M, R, R, M, M
M, R, M, R, M
No dia-a-dia as pessoas e as crianças em particular, dividem, repartem, distribuem coisas. essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida (M) e a de repartir (R) em partes iguais.
A ideia da divisão é de repartir (R) quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
A ideia é de medida (M) quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir. Em seguida assinale a sequência correta.
I – Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
II – Ari comprou 48 figurinhas e vai dividir estas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
III- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
IV – Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
V - Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
R, R, R, R, R
R, R, M, M, R
M, M, M, M, M
R, R, M, M, M
M, M, R, R, R
As crianças desde muito cedo realizam contagens e relacionam pequenas quantidades a essa contagem. Elas contam no dedo, contam com palitos dentre outros objetos. Para sistematizar o processo de contagem, estabelecer a relação número quantidade e compreender o sistema de numeração, o professor pode utilizar o material Dourado.
“Material Dourado é um dos materiais idealizados pela médica e educadora Maria Montessori. Ele tem como foco o trabalho com a matemática. Apesar de ter sido elaborado para o trabalho com aritmética, seguiu os mesmos princípios montessorianos sobre a educação sensorial”. Disponível em: http://pt.wikipedia.org/wiki/Material_Dourado. Acesso em: 07/02/2017.
Leia e analise as alternativas abaixo, em seguida assinale a alternativa que não corresponde a característica ou aplicabilidade desse recurso na sala de aula.
O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?

R, M, R, R, M
M, M, R. R. M
R, R, R, M, M
M, R, R, M, M
M, R, M, R, M
No dia-a-dia as pessoas e as crianças em particular, dividem, repartem, distribuem coisas. essas experiências constituem o ponto de partida para o trabalho com a divisão que por sua vez possui duas ideias: a de medida (M) e a de repartir (R) em partes iguais.
A ideia da divisão é de repartir (R) quando o número de agrupamentos a ser formado é conhecido, e queremos saber a quantidade de elementos em cada agrupamento. Esta ideia vale para divisão exata e para as que sobram reto, ou seja, que não são exatas.
A ideia é de medida (M) quando o número de elementos de cada agrupamento a ser formado é conhecido e precisamos determinar quantos agrupamentos serão formados.
Com base neste estudo, analise as situações problema e identifique se a ideia é de medir ou repartir. Em seguida assinale a sequência correta.
I – Em uma gincana na escola Ana ganhou 9 chocolates. Ela quer repartir com seus 3 irmãos. Quantos chocolates vai receber cada um dos seus irmãos?
II – Ari comprou 48 figurinhas e vai dividir estas figurinhas com 8 colegas. Quantas figurinha cada colega vai ganhar?
III- Seu Antonio tem 35 bolinhas de gude e quer montar saquinhos com 6 bolinhas. Quantos saquinhos ele precisa?
IV – Ari colou 48 figurinhas em um álbum. Em cada página foram coladas 6 figurinhas. Quantas páginas foram utilizadas?
V - Marcela recebeu 120 reais de mesada. Ela quer repartir esse dinheiro em 3 quantias iguais. Um ela vai gastar, a outra vai comprar uma blusa e a outra quantia ela vai por no cofrinho. Quanto vai dar cada uma dessas quantias?
R, R, R, R, R
R, R, M, M, R
M, M, M, M, M
R, R, M, M, M
M, M, R, R, R
As crianças desde muito cedo realizam contagens e relacionam pequenas quantidades a essa contagem. Elas contam no dedo, contam com palitos dentre outros objetos. Para sistematizar o processo de contagem, estabelecer a relação número quantidade e compreender o sistema de numeração, o professor pode utilizar o material Dourado.
“Material Dourado é um dos materiais idealizados pela médica e educadora Maria Montessori. Ele tem como foco o trabalho com a matemática. Apesar de ter sido elaborado para o trabalho com aritmética, seguiu os mesmos princípios montessorianos sobre a educação sensorial”. Disponível em: http://pt.wikipedia.org/wiki/Material_Dourado. Acesso em: 07/02/2017.
Leia e analise as alternativas abaixo, em seguida assinale a alternativa que não corresponde a característica ou aplicabilidade desse recurso na sala de aula.
O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?

R, R, R, R, R
R, R, M, M, R
M, M, M, M, M
R, R, M, M, M
M, M, R, R, R
As crianças desde muito cedo realizam contagens e relacionam pequenas quantidades a essa contagem. Elas contam no dedo, contam com palitos dentre outros objetos. Para sistematizar o processo de contagem, estabelecer a relação número quantidade e compreender o sistema de numeração, o professor pode utilizar o material Dourado.
“Material Dourado é um dos materiais idealizados pela médica e educadora Maria Montessori. Ele tem como foco o trabalho com a matemática. Apesar de ter sido elaborado para o trabalho com aritmética, seguiu os mesmos princípios montessorianos sobre a educação sensorial”. Disponível em: http://pt.wikipedia.org/wiki/Material_Dourado. Acesso em: 07/02/2017.
Leia e analise as alternativas abaixo, em seguida assinale a alternativa que não corresponde a característica ou aplicabilidade desse recurso na sala de aula.
O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?

O Material Dourado é constituído por bastões e contas douradas. Cada bastão representa uma ordem. Ordem das unidades, ordem das dezenas, ordem das centenas e ordem das milhares.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
No material dourado a cada dez cubinhos das unidades trocamos por uma barrinha, subdividida de dez em dez. E a cada dez barrinhas trocamos por uma plaquinha que representa a centena. E a cada dez plaquinhas – cem- trocamos pelo cubo do milhar.
Com o Material Dourado podemos relacionar número e quantidade, realizar as quatro operações básicas, o cálculo de área e volume.
O Material Dourado é composto por cubinhos que representam as unidades, por barrinhas que representam as dezenas, por placas subdivididas em cem cubinhos que representam as centenas e por um cubo grande; que representa a unidade de milhar.
No que se refere a Matemática, no primeiro ciclo, as crianças estabelecem relações que as aproximam de alguns conceitos, descobrem procedimentos simples e desenvolvem atitudes perante a Matemática. Na educação Infantil e nos anos Iniciais do Ensino Fundamental trabalhar com o material concreto é uma forma de apresentar ao aluno uma maneira mais fácil e palpável de como a matemática é utilizada no cotidiano.
Assim, assinale a afirmativa que não é sugestão de atividade desenvolvida com o auxilio do material concreto.
O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.
Em um balde foram colcocados 15.000 litros de água, que correspondem a 3/5 de sua capacidade total. Quantos litros de água serão necessários para preencher todo o balde?

O uso do Tangram desperta a curiosidade, criatividade e interesse. O mesmo poderá ser utilizado no trabalho na identificação das cores, formas, espessura, os conceitos topológicos.
Atividades de leituras e exercícios reforçam a aprendizagem, e, levam o aluno a interpretar o que está sendo posto.
O trabalho com Material Dourado possibilita a compreensão do agrupamento de dez em dez, isto é, do sistema de numeração decimal. O cálculo neste material inicia da direita para a esquerda, na ordem das unidades simples.
O Quadro Valor de Lugar – QVL, é um recurso prático no qual pode-se trabalhar as ordens e classes. Esse procedimento permite trocas, quando se formam grupos em uma determinada base.
O Ábaco é utilizado na sala de aula, para facilitar a compreensão do nosso sistema de numeração e, consequentemente, os cálculos.