O Sistema de Numeração Romana após o sistema decimal é o sistema mais utilizado na educação básica.   Além disso, é utilizado também na representação de datas, séculos, capítulos e volumes de livros, relógios, textos jurídicos e constituições de países e órgãos internacionais entre outros. O número 8 967    escrito no sistema  de numeração romano 

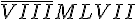
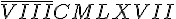
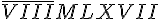
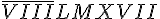
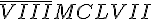
Encontre um número natural que ao ser dividido por 8 resulta um quociente 5 e o resto maior possivel?

Determine M tal que o numero 934M1M seja divisivel por 2 e por 3

Paulo possui um terreno e deseja dividi-lo em lotes quadrados com o maior tamanho possível. Este terreno tem a forma retangular com 40 metros de largura e 60 metros de comprimento. Quantos lotes Paulo terá depois de feita a divisão do terreno?

O instrumento ou ferramenta para provar ou demonstrar uma proposição é o Princípio da Indução Finita (P.I.F.). Então provando por indução finita, a seguinte proposição 4 + 10 + 16 +.....+ (6n-2) = n(3n+1) para todo n , qual das alternativas a seguir, representa a   hipótese DE INDUÇÃO correta:

Com relação ao estudo de Indução, leia as afirmativas a seguir:

I.Iimagine que você está subindo em uma escada sem fim e você pode alcançar o primeiro degrau e se você alcançar um degrau, você pode sempre passar ao degrau seguinte.  Você pode, então, subir tão alto quanto quanto você queira .Desta forma esse exemplifica a Indução.

II.O princípio da indução matemática é uma implicação. A tese desta implicação é uma sentença da forma "P(n) é verdadeira para todos os n inteiros positivos". Portanto, sempre que desejamos demonstrar que alguma propriedade é válida para todo inteiro positivo n, uma tentativa é o uso da indução matemática como técnica de demonstração.

III.Ao desenvolver uma demonstração por indução, estabelecemos inicialmente a veracidade da sentença 1,P(1), que é chamada de base da indução ou passo básico, para a demonstração indutiva. Estabelecer que a sentença é verdadeira constitui o passo indutivo. Quando assumimos que P(k) é verdadeira com o intuito de demonstrar o passo indutivo, P(k) é chamado de suposição indutiva, ou hipótese indutiva

E correto que se afirma em

Considere os números  A e B, estão transcritos no  sistema binário, sendo   A = (10010) e B = (100001) , transcrevendo-os para o sistema  de numeração de base 10 , o valor de  A + B é igual a:

Aritmética (da palavra grega número) é o mais elementar e mais antigo ramo da Matemática. O termo aritmético também é usado para se referir à Teoria dos Números, ramo da Matemática pura que estuda mais profundamente as propriedades dos números em geral, então leia as afirmativas a seguir sobre as operações aritméticas:

 I.“Pedir emprestado” significa fazer trocas: de dezenas por unidades, quando estas não são suficientes; de centenas por dezenas e assim sucessivamente. A denominação “pedir emprestado” não é adequada, porque as quantidades necessárias não estão presentes no número, apenas estão agrupadas, pois nosso sistema de numeração é posicional, de base 10.

 II.Ao multiplicarmos dois números que tem mais de uma ordem, pulamos uma casa por que estamos multiplicando por números de ordem superior, ou seja, quando vamos multiplicar a dezena temos que colocar na respectiva ordem, por isso a expressão “Pular uma casa”. O mesmo ocorre para as outras ordens

 III. Chama-se de “vai um” o transporte de uma ordem para a ordem imediatamente superior, que aqui significa “vai uma dezena”. Quando se somam as dezenas, o “vai um” significa “vai uma centena”, este processo é conhecido como “transporte de reserva”.

E correto que se afirma em:

Se (a + b) + c = a + (b + c), então podemos citar como exemplo: