METODOLOGIA DO ENSINO DA MATEMÁTICA
Observando a operação a seguir , os valores do minuendo e do resto respectivamente são :
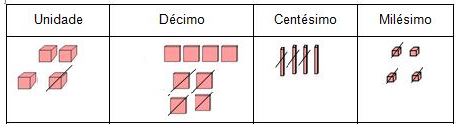
3,431 e 3,411.
4,844 e 3,411.
3,431 e 3,431.
1,433 e 3,411.
1,433 e 3,431.
Ao analisar o esquema a seguir, você entende que ele resume os passos de um processo que denominamos de:
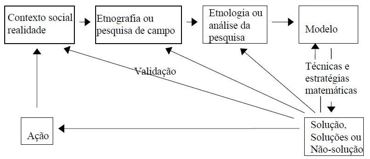
Modelagem Matemática
Resolução de problemas
Pesquisa
Etnomatemática
Questionário
Num acampamento avançado, 30 soldados dispõem de víveres para 60 dias. Se mais 90 soldados chegam ao acampamento, então, por quanto tempo o acampamento estará abastecido?
12
14
11
10
15
Sabemos que na história da Matemática, a álgebra, está presente em várias situações, tais como: equações, números, funções, na geometria, entre outros. Em 1638, o filósofo e Matemático francês René Descartes ( 1596 – 1650 ) usou as primeiras letras do alfabeto para designar os números conhecidos e as últimas letras para incógnitas. Utilizando estas letras, temos os polinômios, em relação a eles, podemos afirmar que as alternativas corretas são:
I – Na expressão 2 x – 3 y, temos um monômio, cujos coeficientes são 2 e – 3.
II – Polinômio é somente uma soma algébrica de binômios.
III – x² + xy +xy + y ² é um trinômio.
IV – Só podemos adicionar ou subtrair polinômios, quando eles forem semelhantes.
V – O Polinômio 8, tem grau 0.
I, IV e V.
III, IV e V.
I, III e V.
II, III e IV.
II, IV e V.
Ao ingressar em uma escola pública que oferece a Educação de Jovens e Adultos, a aluna Marilda, de 38 anos, ficou surpresa ao saber que teria de assistir aulas de artes. Veja o depoimento dela:
“Quando estudei na escola, a educação artística era uma coisa
mecânica, não dava prazer em estudar. Mas fui obrigada a mudar
de opinião ao ingressar nesse colégio (...) De tudo que aprendi,
sei que educação artística não se limita somente à régua e
compasso. Existe muito além dos limites de simples traçados.
Digamos que a arte é infinita e maravilhosa. Simples, completa e
fascinante”.
Neste sentido, é correto afirmar:
I Ajustar esta surpresa é um desafio que, por vezes, mostra-se custoso demais, incorrendo, em muitos casos, no abandono, em nova desistência.
II Como bem pudemos ver no depoimento, ela também precisa ajustar suas expectativas à realidade que encontra quando volta para a escola.
III Com o tempo, através da experiência obtida por meio desta aula e de outras, seu olhar sobre a escola, se transformou.
São corretas as afirmativas:
II apenas.
I, II e III.
I e III apenas.
I e II apenas.
III apenas.
A ausência do domínio da leitura e da escrita, no entanto, não representa ausência de cultura e outros saberes não acadêmicos. Nesse contexto, os projetos pedagógicos para turmas da EJA devem ser pensados de maneira que possam contemplar o multiculturalismo e que sejam capazes de valorizar e reconhecer a complementaridade entre os saberes acadêmicos e os informais (ligados ao contexto sociocultural do educando), a experiência de vida já adquirida pelos discentes e as diferenças entre as formas de conhecimento. O currículo deve abranger temas que possibilitem compreender o contexto em que os alunos vivem, ou seja, que estabeleça o objetivo da educação para adultos integrada à formação profissional. Nesse processo, o professor tem papel fundamental; ele deve atuar como:
um articulador do processo de construção do conhecimento, utilizando um método único e eficiente, ativo, dialógico, crítico e tecnicista, possibilitando uma interação maior entre docente e comunidade e favorecendo o processo de ensino aprendizagem.
um mediador possibilitando uma formação pessoal do indivíduo, dando a ele o direito de entender e intervir na sociedade na qual está inserido, o direito de tornar-se cidadão, de maneira assistemática e esporádica.
um acolhedor das diferenças e as considerar no processo de ensino aprendizagem, reconhecendo que cada estudante aprende de uma forma diferente, desenvolvendo um contexto próprio para ser reconhecido apenas como indivíduo alfabetizado.
um mediador do processo de construção do conhecimento, utilizando um método que seja ativo, dialógico, crítico e criticista, possibilitando uma interação maior entre docente e discente e favorecendo o processo de ensino aprendizagem.
um mediador, facilitador e articulador do conhecimento, aquele que detém toda a informação e saber. Ele deve atuar como um pesquisador, que provoca o aluno a ser também curioso e descobrir a partir de seus próprios questionamentos, que deverá negociar os conhecimentos adquiridos e apoiar os estudantes e juntos sintetizarem o conhecimento compartilhado.
De acordo com o exposto e considerando a etnomatemática para o repensar o fazer pedagógico dos professores, analise as afirmativas a seguir.
I. A Educação Matemática, neste enfoque, contempla o saber oriundo do cotidiano, a qual acredita que está imbuído de saberes e fazeres próprios da cultura.
II. Tem a pretensão de substituir a matemática acadêmica, que é absolutamente inútil na sociedade, considerando a educação multicultural como uma possibilidade a qual valoriza e reconhece como legítimo o saber matemático oriundo das diversas culturas.
III. Tem como objetivo conectar a realidade com a matemática, promovendo o estudo a partir do mundo vivido/concreto para a análise dos conteúdos abstratos e a resolução de problemas que propiciam a compreensão e a constituição de saberes e alternativas para o contexto.
IV. O termo etnomatemática foi constituído por Ubiratan D.Ambrósio. Para compor a palavra etnomatemática, utilizam‐se as raízes tica, matema e etn” para significar que há várias maneiras, técnicas, habilidades (ticas) de explicar, de entender, de lidar e de conviver com (matema) distintos contextos naturais e socioeconômicos da realidade (etnos).
Estão corretas as afirmativas
I, II e III
I, II e IV
II e IV
II, III e IV
I, III e IV
A Etnomatemática surgiu na década de 1970, com base em críticas sociais acerca do ensino tradicional da Matemática, como a análise das práticas matemáticas em seus diferentes contextos culturais. Mais adiante, o conceito passou a designar as diferenças culturais nas diferentes formas de conhecimento, uma junção dos termos techné, mátema e etno, esta proposta educacional defende que a Matemática deve ser explicada e entendida dentro de um contexto cultural próprio, tendo Ubiratan DAmbrósio como precursor e idealizador no Brasil.
Sendo assim, analise as alternativas a seguir e assinale a alternativa que indica as que estão corretas:
I- A Etnomatemática é uma proposta educacional que aborda as relações interculturais da Matemática, em que a disciplina deve ser compreendida para além da constituição social, mas também como construção histórica e política.
II- Muitas vezes, a influência recíproca entre duas ou mais culturas não é levada em consideração na historiografia da Matemática, o que traz implicações na educação. Existe a enorme tendência de se trabalhar a Matemática da cultura predominante, sem a influência do ambiente cultural do aluno.
III- A Etnomatemática defende que se enfatizem as ações pedagógicas construídas dentro do contexto sociocultural dos educandos, levando-se em consideração os distintos grupos culturais. Assim sendo, são enaltecidos os conceitos matemáticos informais desenvolvidos pelos alunos através de seus conhecimentos, fora da vivência escolar.
IV- Etnomatemática valoriza as diferenças e defende que toda construção do conhecimento matemático, está intimamente relacionado com a tradição, sociedade e cultura de cada povo. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
V- O ensino da matemática na perspectiva Etnomatemática contempla as experiências cotidianas e, por isso, enriquece a relação entre teoria e prática, onde a linguagem matemática está presente nas mais diversas atividades humanas, como nas artes, arquitetura, música, dança, esporte, engenharia etc., e faz parte do contexto da sociedade na qual o indivíduo está inserido, estando, assim, relacionada ao social e cultural.
A respeito dessas asserções, assinale a alternativa correta:
Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:
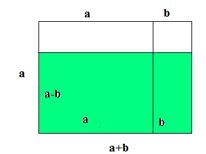
( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:
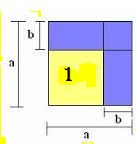

3,431 e 3,411.
4,844 e 3,411.
3,431 e 3,431.
1,433 e 3,411.
1,433 e 3,431.
Ao analisar o esquema a seguir, você entende que ele resume os passos de um processo que denominamos de:

Modelagem Matemática
Resolução de problemas
Pesquisa
Etnomatemática
Questionário
Num acampamento avançado, 30 soldados dispõem de víveres para 60 dias. Se mais 90 soldados chegam ao acampamento, então, por quanto tempo o acampamento estará abastecido?
12
14
11
10
15
Sabemos que na história da Matemática, a álgebra, está presente em várias situações, tais como: equações, números, funções, na geometria, entre outros. Em 1638, o filósofo e Matemático francês René Descartes ( 1596 – 1650 ) usou as primeiras letras do alfabeto para designar os números conhecidos e as últimas letras para incógnitas. Utilizando estas letras, temos os polinômios, em relação a eles, podemos afirmar que as alternativas corretas são:
I – Na expressão 2 x – 3 y, temos um monômio, cujos coeficientes são 2 e – 3.
II – Polinômio é somente uma soma algébrica de binômios.
III – x² + xy +xy + y ² é um trinômio.
IV – Só podemos adicionar ou subtrair polinômios, quando eles forem semelhantes.
V – O Polinômio 8, tem grau 0.
I, IV e V.
III, IV e V.
I, III e V.
II, III e IV.
II, IV e V.
Ao ingressar em uma escola pública que oferece a Educação de Jovens e Adultos, a aluna Marilda, de 38 anos, ficou surpresa ao saber que teria de assistir aulas de artes. Veja o depoimento dela:
“Quando estudei na escola, a educação artística era uma coisa
mecânica, não dava prazer em estudar. Mas fui obrigada a mudar
de opinião ao ingressar nesse colégio (...) De tudo que aprendi,
sei que educação artística não se limita somente à régua e
compasso. Existe muito além dos limites de simples traçados.
Digamos que a arte é infinita e maravilhosa. Simples, completa e
fascinante”.
Neste sentido, é correto afirmar:
I Ajustar esta surpresa é um desafio que, por vezes, mostra-se custoso demais, incorrendo, em muitos casos, no abandono, em nova desistência.
II Como bem pudemos ver no depoimento, ela também precisa ajustar suas expectativas à realidade que encontra quando volta para a escola.
III Com o tempo, através da experiência obtida por meio desta aula e de outras, seu olhar sobre a escola, se transformou.
São corretas as afirmativas:
II apenas.
I, II e III.
I e III apenas.
I e II apenas.
III apenas.
A ausência do domínio da leitura e da escrita, no entanto, não representa ausência de cultura e outros saberes não acadêmicos. Nesse contexto, os projetos pedagógicos para turmas da EJA devem ser pensados de maneira que possam contemplar o multiculturalismo e que sejam capazes de valorizar e reconhecer a complementaridade entre os saberes acadêmicos e os informais (ligados ao contexto sociocultural do educando), a experiência de vida já adquirida pelos discentes e as diferenças entre as formas de conhecimento. O currículo deve abranger temas que possibilitem compreender o contexto em que os alunos vivem, ou seja, que estabeleça o objetivo da educação para adultos integrada à formação profissional. Nesse processo, o professor tem papel fundamental; ele deve atuar como:
um articulador do processo de construção do conhecimento, utilizando um método único e eficiente, ativo, dialógico, crítico e tecnicista, possibilitando uma interação maior entre docente e comunidade e favorecendo o processo de ensino aprendizagem.
um mediador possibilitando uma formação pessoal do indivíduo, dando a ele o direito de entender e intervir na sociedade na qual está inserido, o direito de tornar-se cidadão, de maneira assistemática e esporádica.
um acolhedor das diferenças e as considerar no processo de ensino aprendizagem, reconhecendo que cada estudante aprende de uma forma diferente, desenvolvendo um contexto próprio para ser reconhecido apenas como indivíduo alfabetizado.
um mediador do processo de construção do conhecimento, utilizando um método que seja ativo, dialógico, crítico e criticista, possibilitando uma interação maior entre docente e discente e favorecendo o processo de ensino aprendizagem.
um mediador, facilitador e articulador do conhecimento, aquele que detém toda a informação e saber. Ele deve atuar como um pesquisador, que provoca o aluno a ser também curioso e descobrir a partir de seus próprios questionamentos, que deverá negociar os conhecimentos adquiridos e apoiar os estudantes e juntos sintetizarem o conhecimento compartilhado.
De acordo com o exposto e considerando a etnomatemática para o repensar o fazer pedagógico dos professores, analise as afirmativas a seguir.
I. A Educação Matemática, neste enfoque, contempla o saber oriundo do cotidiano, a qual acredita que está imbuído de saberes e fazeres próprios da cultura.
II. Tem a pretensão de substituir a matemática acadêmica, que é absolutamente inútil na sociedade, considerando a educação multicultural como uma possibilidade a qual valoriza e reconhece como legítimo o saber matemático oriundo das diversas culturas.
III. Tem como objetivo conectar a realidade com a matemática, promovendo o estudo a partir do mundo vivido/concreto para a análise dos conteúdos abstratos e a resolução de problemas que propiciam a compreensão e a constituição de saberes e alternativas para o contexto.
IV. O termo etnomatemática foi constituído por Ubiratan D.Ambrósio. Para compor a palavra etnomatemática, utilizam‐se as raízes tica, matema e etn” para significar que há várias maneiras, técnicas, habilidades (ticas) de explicar, de entender, de lidar e de conviver com (matema) distintos contextos naturais e socioeconômicos da realidade (etnos).
Estão corretas as afirmativas
I, II e III
I, II e IV
II e IV
II, III e IV
I, III e IV
A Etnomatemática surgiu na década de 1970, com base em críticas sociais acerca do ensino tradicional da Matemática, como a análise das práticas matemáticas em seus diferentes contextos culturais. Mais adiante, o conceito passou a designar as diferenças culturais nas diferentes formas de conhecimento, uma junção dos termos techné, mátema e etno, esta proposta educacional defende que a Matemática deve ser explicada e entendida dentro de um contexto cultural próprio, tendo Ubiratan DAmbrósio como precursor e idealizador no Brasil.
Sendo assim, analise as alternativas a seguir e assinale a alternativa que indica as que estão corretas:
I- A Etnomatemática é uma proposta educacional que aborda as relações interculturais da Matemática, em que a disciplina deve ser compreendida para além da constituição social, mas também como construção histórica e política.
II- Muitas vezes, a influência recíproca entre duas ou mais culturas não é levada em consideração na historiografia da Matemática, o que traz implicações na educação. Existe a enorme tendência de se trabalhar a Matemática da cultura predominante, sem a influência do ambiente cultural do aluno.
III- A Etnomatemática defende que se enfatizem as ações pedagógicas construídas dentro do contexto sociocultural dos educandos, levando-se em consideração os distintos grupos culturais. Assim sendo, são enaltecidos os conceitos matemáticos informais desenvolvidos pelos alunos através de seus conhecimentos, fora da vivência escolar.
IV- Etnomatemática valoriza as diferenças e defende que toda construção do conhecimento matemático, está intimamente relacionado com a tradição, sociedade e cultura de cada povo. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
V- O ensino da matemática na perspectiva Etnomatemática contempla as experiências cotidianas e, por isso, enriquece a relação entre teoria e prática, onde a linguagem matemática está presente nas mais diversas atividades humanas, como nas artes, arquitetura, música, dança, esporte, engenharia etc., e faz parte do contexto da sociedade na qual o indivíduo está inserido, estando, assim, relacionada ao social e cultural.
A respeito dessas asserções, assinale a alternativa correta:
Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:

( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:


Modelagem Matemática
Resolução de problemas
Pesquisa
Etnomatemática
Questionário
Num acampamento avançado, 30 soldados dispõem de víveres para 60 dias. Se mais 90 soldados chegam ao acampamento, então, por quanto tempo o acampamento estará abastecido?
12
14
11
10
15
Sabemos que na história da Matemática, a álgebra, está presente em várias situações, tais como: equações, números, funções, na geometria, entre outros. Em 1638, o filósofo e Matemático francês René Descartes ( 1596 – 1650 ) usou as primeiras letras do alfabeto para designar os números conhecidos e as últimas letras para incógnitas. Utilizando estas letras, temos os polinômios, em relação a eles, podemos afirmar que as alternativas corretas são:
I – Na expressão 2 x – 3 y, temos um monômio, cujos coeficientes são 2 e – 3.
II – Polinômio é somente uma soma algébrica de binômios.
III – x² + xy +xy + y ² é um trinômio.
IV – Só podemos adicionar ou subtrair polinômios, quando eles forem semelhantes.
V – O Polinômio 8, tem grau 0.
I, IV e V.
III, IV e V.
I, III e V.
II, III e IV.
II, IV e V.
Ao ingressar em uma escola pública que oferece a Educação de Jovens e Adultos, a aluna Marilda, de 38 anos, ficou surpresa ao saber que teria de assistir aulas de artes. Veja o depoimento dela:
“Quando estudei na escola, a educação artística era uma coisa
mecânica, não dava prazer em estudar. Mas fui obrigada a mudar
de opinião ao ingressar nesse colégio (...) De tudo que aprendi,
sei que educação artística não se limita somente à régua e
compasso. Existe muito além dos limites de simples traçados.
Digamos que a arte é infinita e maravilhosa. Simples, completa e
fascinante”.
Neste sentido, é correto afirmar:
I Ajustar esta surpresa é um desafio que, por vezes, mostra-se custoso demais, incorrendo, em muitos casos, no abandono, em nova desistência.
II Como bem pudemos ver no depoimento, ela também precisa ajustar suas expectativas à realidade que encontra quando volta para a escola.
III Com o tempo, através da experiência obtida por meio desta aula e de outras, seu olhar sobre a escola, se transformou.
São corretas as afirmativas:
II apenas.
I, II e III.
I e III apenas.
I e II apenas.
III apenas.
A ausência do domínio da leitura e da escrita, no entanto, não representa ausência de cultura e outros saberes não acadêmicos. Nesse contexto, os projetos pedagógicos para turmas da EJA devem ser pensados de maneira que possam contemplar o multiculturalismo e que sejam capazes de valorizar e reconhecer a complementaridade entre os saberes acadêmicos e os informais (ligados ao contexto sociocultural do educando), a experiência de vida já adquirida pelos discentes e as diferenças entre as formas de conhecimento. O currículo deve abranger temas que possibilitem compreender o contexto em que os alunos vivem, ou seja, que estabeleça o objetivo da educação para adultos integrada à formação profissional. Nesse processo, o professor tem papel fundamental; ele deve atuar como:
um articulador do processo de construção do conhecimento, utilizando um método único e eficiente, ativo, dialógico, crítico e tecnicista, possibilitando uma interação maior entre docente e comunidade e favorecendo o processo de ensino aprendizagem.
um mediador possibilitando uma formação pessoal do indivíduo, dando a ele o direito de entender e intervir na sociedade na qual está inserido, o direito de tornar-se cidadão, de maneira assistemática e esporádica.
um acolhedor das diferenças e as considerar no processo de ensino aprendizagem, reconhecendo que cada estudante aprende de uma forma diferente, desenvolvendo um contexto próprio para ser reconhecido apenas como indivíduo alfabetizado.
um mediador do processo de construção do conhecimento, utilizando um método que seja ativo, dialógico, crítico e criticista, possibilitando uma interação maior entre docente e discente e favorecendo o processo de ensino aprendizagem.
um mediador, facilitador e articulador do conhecimento, aquele que detém toda a informação e saber. Ele deve atuar como um pesquisador, que provoca o aluno a ser também curioso e descobrir a partir de seus próprios questionamentos, que deverá negociar os conhecimentos adquiridos e apoiar os estudantes e juntos sintetizarem o conhecimento compartilhado.
De acordo com o exposto e considerando a etnomatemática para o repensar o fazer pedagógico dos professores, analise as afirmativas a seguir.
I. A Educação Matemática, neste enfoque, contempla o saber oriundo do cotidiano, a qual acredita que está imbuído de saberes e fazeres próprios da cultura.
II. Tem a pretensão de substituir a matemática acadêmica, que é absolutamente inútil na sociedade, considerando a educação multicultural como uma possibilidade a qual valoriza e reconhece como legítimo o saber matemático oriundo das diversas culturas.
III. Tem como objetivo conectar a realidade com a matemática, promovendo o estudo a partir do mundo vivido/concreto para a análise dos conteúdos abstratos e a resolução de problemas que propiciam a compreensão e a constituição de saberes e alternativas para o contexto.
IV. O termo etnomatemática foi constituído por Ubiratan D.Ambrósio. Para compor a palavra etnomatemática, utilizam‐se as raízes tica, matema e etn” para significar que há várias maneiras, técnicas, habilidades (ticas) de explicar, de entender, de lidar e de conviver com (matema) distintos contextos naturais e socioeconômicos da realidade (etnos).
Estão corretas as afirmativas
I, II e III
I, II e IV
II e IV
II, III e IV
I, III e IV
A Etnomatemática surgiu na década de 1970, com base em críticas sociais acerca do ensino tradicional da Matemática, como a análise das práticas matemáticas em seus diferentes contextos culturais. Mais adiante, o conceito passou a designar as diferenças culturais nas diferentes formas de conhecimento, uma junção dos termos techné, mátema e etno, esta proposta educacional defende que a Matemática deve ser explicada e entendida dentro de um contexto cultural próprio, tendo Ubiratan DAmbrósio como precursor e idealizador no Brasil.
Sendo assim, analise as alternativas a seguir e assinale a alternativa que indica as que estão corretas:
I- A Etnomatemática é uma proposta educacional que aborda as relações interculturais da Matemática, em que a disciplina deve ser compreendida para além da constituição social, mas também como construção histórica e política.
II- Muitas vezes, a influência recíproca entre duas ou mais culturas não é levada em consideração na historiografia da Matemática, o que traz implicações na educação. Existe a enorme tendência de se trabalhar a Matemática da cultura predominante, sem a influência do ambiente cultural do aluno.
III- A Etnomatemática defende que se enfatizem as ações pedagógicas construídas dentro do contexto sociocultural dos educandos, levando-se em consideração os distintos grupos culturais. Assim sendo, são enaltecidos os conceitos matemáticos informais desenvolvidos pelos alunos através de seus conhecimentos, fora da vivência escolar.
IV- Etnomatemática valoriza as diferenças e defende que toda construção do conhecimento matemático, está intimamente relacionado com a tradição, sociedade e cultura de cada povo. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
V- O ensino da matemática na perspectiva Etnomatemática contempla as experiências cotidianas e, por isso, enriquece a relação entre teoria e prática, onde a linguagem matemática está presente nas mais diversas atividades humanas, como nas artes, arquitetura, música, dança, esporte, engenharia etc., e faz parte do contexto da sociedade na qual o indivíduo está inserido, estando, assim, relacionada ao social e cultural.
A respeito dessas asserções, assinale a alternativa correta:
Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:

( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:

12
14
11
10
15
Sabemos que na história da Matemática, a álgebra, está presente em várias situações, tais como: equações, números, funções, na geometria, entre outros. Em 1638, o filósofo e Matemático francês René Descartes ( 1596 – 1650 ) usou as primeiras letras do alfabeto para designar os números conhecidos e as últimas letras para incógnitas. Utilizando estas letras, temos os polinômios, em relação a eles, podemos afirmar que as alternativas corretas são:
I – Na expressão 2 x – 3 y, temos um monômio, cujos coeficientes são 2 e – 3.
II – Polinômio é somente uma soma algébrica de binômios.
III – x² + xy +xy + y ² é um trinômio.
IV – Só podemos adicionar ou subtrair polinômios, quando eles forem semelhantes.
V – O Polinômio 8, tem grau 0.
I, IV e V.
III, IV e V.
I, III e V.
II, III e IV.
II, IV e V.
Ao ingressar em uma escola pública que oferece a Educação de Jovens e Adultos, a aluna Marilda, de 38 anos, ficou surpresa ao saber que teria de assistir aulas de artes. Veja o depoimento dela:
“Quando estudei na escola, a educação artística era uma coisa
mecânica, não dava prazer em estudar. Mas fui obrigada a mudar
de opinião ao ingressar nesse colégio (...) De tudo que aprendi,
sei que educação artística não se limita somente à régua e
compasso. Existe muito além dos limites de simples traçados.
Digamos que a arte é infinita e maravilhosa. Simples, completa e
fascinante”.
Neste sentido, é correto afirmar:
I Ajustar esta surpresa é um desafio que, por vezes, mostra-se custoso demais, incorrendo, em muitos casos, no abandono, em nova desistência.
II Como bem pudemos ver no depoimento, ela também precisa ajustar suas expectativas à realidade que encontra quando volta para a escola.
III Com o tempo, através da experiência obtida por meio desta aula e de outras, seu olhar sobre a escola, se transformou.
São corretas as afirmativas:
II apenas.
I, II e III.
I e III apenas.
I e II apenas.
III apenas.
A ausência do domínio da leitura e da escrita, no entanto, não representa ausência de cultura e outros saberes não acadêmicos. Nesse contexto, os projetos pedagógicos para turmas da EJA devem ser pensados de maneira que possam contemplar o multiculturalismo e que sejam capazes de valorizar e reconhecer a complementaridade entre os saberes acadêmicos e os informais (ligados ao contexto sociocultural do educando), a experiência de vida já adquirida pelos discentes e as diferenças entre as formas de conhecimento. O currículo deve abranger temas que possibilitem compreender o contexto em que os alunos vivem, ou seja, que estabeleça o objetivo da educação para adultos integrada à formação profissional. Nesse processo, o professor tem papel fundamental; ele deve atuar como:
um articulador do processo de construção do conhecimento, utilizando um método único e eficiente, ativo, dialógico, crítico e tecnicista, possibilitando uma interação maior entre docente e comunidade e favorecendo o processo de ensino aprendizagem.
um mediador possibilitando uma formação pessoal do indivíduo, dando a ele o direito de entender e intervir na sociedade na qual está inserido, o direito de tornar-se cidadão, de maneira assistemática e esporádica.
um acolhedor das diferenças e as considerar no processo de ensino aprendizagem, reconhecendo que cada estudante aprende de uma forma diferente, desenvolvendo um contexto próprio para ser reconhecido apenas como indivíduo alfabetizado.
um mediador do processo de construção do conhecimento, utilizando um método que seja ativo, dialógico, crítico e criticista, possibilitando uma interação maior entre docente e discente e favorecendo o processo de ensino aprendizagem.
um mediador, facilitador e articulador do conhecimento, aquele que detém toda a informação e saber. Ele deve atuar como um pesquisador, que provoca o aluno a ser também curioso e descobrir a partir de seus próprios questionamentos, que deverá negociar os conhecimentos adquiridos e apoiar os estudantes e juntos sintetizarem o conhecimento compartilhado.
De acordo com o exposto e considerando a etnomatemática para o repensar o fazer pedagógico dos professores, analise as afirmativas a seguir.
I. A Educação Matemática, neste enfoque, contempla o saber oriundo do cotidiano, a qual acredita que está imbuído de saberes e fazeres próprios da cultura.
II. Tem a pretensão de substituir a matemática acadêmica, que é absolutamente inútil na sociedade, considerando a educação multicultural como uma possibilidade a qual valoriza e reconhece como legítimo o saber matemático oriundo das diversas culturas.
III. Tem como objetivo conectar a realidade com a matemática, promovendo o estudo a partir do mundo vivido/concreto para a análise dos conteúdos abstratos e a resolução de problemas que propiciam a compreensão e a constituição de saberes e alternativas para o contexto.
IV. O termo etnomatemática foi constituído por Ubiratan D.Ambrósio. Para compor a palavra etnomatemática, utilizam‐se as raízes tica, matema e etn” para significar que há várias maneiras, técnicas, habilidades (ticas) de explicar, de entender, de lidar e de conviver com (matema) distintos contextos naturais e socioeconômicos da realidade (etnos).
Estão corretas as afirmativas
I, II e III
I, II e IV
II e IV
II, III e IV
I, III e IV
A Etnomatemática surgiu na década de 1970, com base em críticas sociais acerca do ensino tradicional da Matemática, como a análise das práticas matemáticas em seus diferentes contextos culturais. Mais adiante, o conceito passou a designar as diferenças culturais nas diferentes formas de conhecimento, uma junção dos termos techné, mátema e etno, esta proposta educacional defende que a Matemática deve ser explicada e entendida dentro de um contexto cultural próprio, tendo Ubiratan DAmbrósio como precursor e idealizador no Brasil.
Sendo assim, analise as alternativas a seguir e assinale a alternativa que indica as que estão corretas:
I- A Etnomatemática é uma proposta educacional que aborda as relações interculturais da Matemática, em que a disciplina deve ser compreendida para além da constituição social, mas também como construção histórica e política.
II- Muitas vezes, a influência recíproca entre duas ou mais culturas não é levada em consideração na historiografia da Matemática, o que traz implicações na educação. Existe a enorme tendência de se trabalhar a Matemática da cultura predominante, sem a influência do ambiente cultural do aluno.
III- A Etnomatemática defende que se enfatizem as ações pedagógicas construídas dentro do contexto sociocultural dos educandos, levando-se em consideração os distintos grupos culturais. Assim sendo, são enaltecidos os conceitos matemáticos informais desenvolvidos pelos alunos através de seus conhecimentos, fora da vivência escolar.
IV- Etnomatemática valoriza as diferenças e defende que toda construção do conhecimento matemático, está intimamente relacionado com a tradição, sociedade e cultura de cada povo. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
V- O ensino da matemática na perspectiva Etnomatemática contempla as experiências cotidianas e, por isso, enriquece a relação entre teoria e prática, onde a linguagem matemática está presente nas mais diversas atividades humanas, como nas artes, arquitetura, música, dança, esporte, engenharia etc., e faz parte do contexto da sociedade na qual o indivíduo está inserido, estando, assim, relacionada ao social e cultural.
A respeito dessas asserções, assinale a alternativa correta:
Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:

( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:

I, IV e V.
III, IV e V.
I, III e V.
II, III e IV.
II, IV e V.
Ao ingressar em uma escola pública que oferece a Educação de Jovens e Adultos, a aluna Marilda, de 38 anos, ficou surpresa ao saber que teria de assistir aulas de artes. Veja o depoimento dela:
“Quando estudei na escola, a educação artística era uma coisa
mecânica, não dava prazer em estudar. Mas fui obrigada a mudar
de opinião ao ingressar nesse colégio (...) De tudo que aprendi,
sei que educação artística não se limita somente à régua e
compasso. Existe muito além dos limites de simples traçados.
Digamos que a arte é infinita e maravilhosa. Simples, completa e
fascinante”.
Neste sentido, é correto afirmar:
I Ajustar esta surpresa é um desafio que, por vezes, mostra-se custoso demais, incorrendo, em muitos casos, no abandono, em nova desistência.
II Como bem pudemos ver no depoimento, ela também precisa ajustar suas expectativas à realidade que encontra quando volta para a escola.
III Com o tempo, através da experiência obtida por meio desta aula e de outras, seu olhar sobre a escola, se transformou.
São corretas as afirmativas:
II apenas.
I, II e III.
I e III apenas.
I e II apenas.
III apenas.
A ausência do domínio da leitura e da escrita, no entanto, não representa ausência de cultura e outros saberes não acadêmicos. Nesse contexto, os projetos pedagógicos para turmas da EJA devem ser pensados de maneira que possam contemplar o multiculturalismo e que sejam capazes de valorizar e reconhecer a complementaridade entre os saberes acadêmicos e os informais (ligados ao contexto sociocultural do educando), a experiência de vida já adquirida pelos discentes e as diferenças entre as formas de conhecimento. O currículo deve abranger temas que possibilitem compreender o contexto em que os alunos vivem, ou seja, que estabeleça o objetivo da educação para adultos integrada à formação profissional. Nesse processo, o professor tem papel fundamental; ele deve atuar como:
um articulador do processo de construção do conhecimento, utilizando um método único e eficiente, ativo, dialógico, crítico e tecnicista, possibilitando uma interação maior entre docente e comunidade e favorecendo o processo de ensino aprendizagem.
um mediador possibilitando uma formação pessoal do indivíduo, dando a ele o direito de entender e intervir na sociedade na qual está inserido, o direito de tornar-se cidadão, de maneira assistemática e esporádica.
um acolhedor das diferenças e as considerar no processo de ensino aprendizagem, reconhecendo que cada estudante aprende de uma forma diferente, desenvolvendo um contexto próprio para ser reconhecido apenas como indivíduo alfabetizado.
um mediador do processo de construção do conhecimento, utilizando um método que seja ativo, dialógico, crítico e criticista, possibilitando uma interação maior entre docente e discente e favorecendo o processo de ensino aprendizagem.
um mediador, facilitador e articulador do conhecimento, aquele que detém toda a informação e saber. Ele deve atuar como um pesquisador, que provoca o aluno a ser também curioso e descobrir a partir de seus próprios questionamentos, que deverá negociar os conhecimentos adquiridos e apoiar os estudantes e juntos sintetizarem o conhecimento compartilhado.
De acordo com o exposto e considerando a etnomatemática para o repensar o fazer pedagógico dos professores, analise as afirmativas a seguir.
I. A Educação Matemática, neste enfoque, contempla o saber oriundo do cotidiano, a qual acredita que está imbuído de saberes e fazeres próprios da cultura.
II. Tem a pretensão de substituir a matemática acadêmica, que é absolutamente inútil na sociedade, considerando a educação multicultural como uma possibilidade a qual valoriza e reconhece como legítimo o saber matemático oriundo das diversas culturas.
III. Tem como objetivo conectar a realidade com a matemática, promovendo o estudo a partir do mundo vivido/concreto para a análise dos conteúdos abstratos e a resolução de problemas que propiciam a compreensão e a constituição de saberes e alternativas para o contexto.
IV. O termo etnomatemática foi constituído por Ubiratan D.Ambrósio. Para compor a palavra etnomatemática, utilizam‐se as raízes tica, matema e etn” para significar que há várias maneiras, técnicas, habilidades (ticas) de explicar, de entender, de lidar e de conviver com (matema) distintos contextos naturais e socioeconômicos da realidade (etnos).
Estão corretas as afirmativas
I, II e III
I, II e IV
II e IV
II, III e IV
I, III e IV
A Etnomatemática surgiu na década de 1970, com base em críticas sociais acerca do ensino tradicional da Matemática, como a análise das práticas matemáticas em seus diferentes contextos culturais. Mais adiante, o conceito passou a designar as diferenças culturais nas diferentes formas de conhecimento, uma junção dos termos techné, mátema e etno, esta proposta educacional defende que a Matemática deve ser explicada e entendida dentro de um contexto cultural próprio, tendo Ubiratan DAmbrósio como precursor e idealizador no Brasil.
Sendo assim, analise as alternativas a seguir e assinale a alternativa que indica as que estão corretas:
I- A Etnomatemática é uma proposta educacional que aborda as relações interculturais da Matemática, em que a disciplina deve ser compreendida para além da constituição social, mas também como construção histórica e política.
II- Muitas vezes, a influência recíproca entre duas ou mais culturas não é levada em consideração na historiografia da Matemática, o que traz implicações na educação. Existe a enorme tendência de se trabalhar a Matemática da cultura predominante, sem a influência do ambiente cultural do aluno.
III- A Etnomatemática defende que se enfatizem as ações pedagógicas construídas dentro do contexto sociocultural dos educandos, levando-se em consideração os distintos grupos culturais. Assim sendo, são enaltecidos os conceitos matemáticos informais desenvolvidos pelos alunos através de seus conhecimentos, fora da vivência escolar.
IV- Etnomatemática valoriza as diferenças e defende que toda construção do conhecimento matemático, está intimamente relacionado com a tradição, sociedade e cultura de cada povo. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
V- O ensino da matemática na perspectiva Etnomatemática contempla as experiências cotidianas e, por isso, enriquece a relação entre teoria e prática, onde a linguagem matemática está presente nas mais diversas atividades humanas, como nas artes, arquitetura, música, dança, esporte, engenharia etc., e faz parte do contexto da sociedade na qual o indivíduo está inserido, estando, assim, relacionada ao social e cultural.
A respeito dessas asserções, assinale a alternativa correta:
Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:

( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:

II apenas.
I, II e III.
I e III apenas.
I e II apenas.
III apenas.
A ausência do domínio da leitura e da escrita, no entanto, não representa ausência de cultura e outros saberes não acadêmicos. Nesse contexto, os projetos pedagógicos para turmas da EJA devem ser pensados de maneira que possam contemplar o multiculturalismo e que sejam capazes de valorizar e reconhecer a complementaridade entre os saberes acadêmicos e os informais (ligados ao contexto sociocultural do educando), a experiência de vida já adquirida pelos discentes e as diferenças entre as formas de conhecimento. O currículo deve abranger temas que possibilitem compreender o contexto em que os alunos vivem, ou seja, que estabeleça o objetivo da educação para adultos integrada à formação profissional. Nesse processo, o professor tem papel fundamental; ele deve atuar como:
um articulador do processo de construção do conhecimento, utilizando um método único e eficiente, ativo, dialógico, crítico e tecnicista, possibilitando uma interação maior entre docente e comunidade e favorecendo o processo de ensino aprendizagem.
um mediador possibilitando uma formação pessoal do indivíduo, dando a ele o direito de entender e intervir na sociedade na qual está inserido, o direito de tornar-se cidadão, de maneira assistemática e esporádica.
um acolhedor das diferenças e as considerar no processo de ensino aprendizagem, reconhecendo que cada estudante aprende de uma forma diferente, desenvolvendo um contexto próprio para ser reconhecido apenas como indivíduo alfabetizado.
um mediador do processo de construção do conhecimento, utilizando um método que seja ativo, dialógico, crítico e criticista, possibilitando uma interação maior entre docente e discente e favorecendo o processo de ensino aprendizagem.
um mediador, facilitador e articulador do conhecimento, aquele que detém toda a informação e saber. Ele deve atuar como um pesquisador, que provoca o aluno a ser também curioso e descobrir a partir de seus próprios questionamentos, que deverá negociar os conhecimentos adquiridos e apoiar os estudantes e juntos sintetizarem o conhecimento compartilhado.
De acordo com o exposto e considerando a etnomatemática para o repensar o fazer pedagógico dos professores, analise as afirmativas a seguir.
I. A Educação Matemática, neste enfoque, contempla o saber oriundo do cotidiano, a qual acredita que está imbuído de saberes e fazeres próprios da cultura.
II. Tem a pretensão de substituir a matemática acadêmica, que é absolutamente inútil na sociedade, considerando a educação multicultural como uma possibilidade a qual valoriza e reconhece como legítimo o saber matemático oriundo das diversas culturas.
III. Tem como objetivo conectar a realidade com a matemática, promovendo o estudo a partir do mundo vivido/concreto para a análise dos conteúdos abstratos e a resolução de problemas que propiciam a compreensão e a constituição de saberes e alternativas para o contexto.
IV. O termo etnomatemática foi constituído por Ubiratan D.Ambrósio. Para compor a palavra etnomatemática, utilizam‐se as raízes tica, matema e etn” para significar que há várias maneiras, técnicas, habilidades (ticas) de explicar, de entender, de lidar e de conviver com (matema) distintos contextos naturais e socioeconômicos da realidade (etnos).
Estão corretas as afirmativas
I, II e III
I, II e IV
II e IV
II, III e IV
I, III e IV
A Etnomatemática surgiu na década de 1970, com base em críticas sociais acerca do ensino tradicional da Matemática, como a análise das práticas matemáticas em seus diferentes contextos culturais. Mais adiante, o conceito passou a designar as diferenças culturais nas diferentes formas de conhecimento, uma junção dos termos techné, mátema e etno, esta proposta educacional defende que a Matemática deve ser explicada e entendida dentro de um contexto cultural próprio, tendo Ubiratan DAmbrósio como precursor e idealizador no Brasil.
Sendo assim, analise as alternativas a seguir e assinale a alternativa que indica as que estão corretas:
I- A Etnomatemática é uma proposta educacional que aborda as relações interculturais da Matemática, em que a disciplina deve ser compreendida para além da constituição social, mas também como construção histórica e política.
II- Muitas vezes, a influência recíproca entre duas ou mais culturas não é levada em consideração na historiografia da Matemática, o que traz implicações na educação. Existe a enorme tendência de se trabalhar a Matemática da cultura predominante, sem a influência do ambiente cultural do aluno.
III- A Etnomatemática defende que se enfatizem as ações pedagógicas construídas dentro do contexto sociocultural dos educandos, levando-se em consideração os distintos grupos culturais. Assim sendo, são enaltecidos os conceitos matemáticos informais desenvolvidos pelos alunos através de seus conhecimentos, fora da vivência escolar.
IV- Etnomatemática valoriza as diferenças e defende que toda construção do conhecimento matemático, está intimamente relacionado com a tradição, sociedade e cultura de cada povo. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
V- O ensino da matemática na perspectiva Etnomatemática contempla as experiências cotidianas e, por isso, enriquece a relação entre teoria e prática, onde a linguagem matemática está presente nas mais diversas atividades humanas, como nas artes, arquitetura, música, dança, esporte, engenharia etc., e faz parte do contexto da sociedade na qual o indivíduo está inserido, estando, assim, relacionada ao social e cultural.
A respeito dessas asserções, assinale a alternativa correta:
Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:

( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:

um articulador do processo de construção do conhecimento, utilizando um método único e eficiente, ativo, dialógico, crítico e tecnicista, possibilitando uma interação maior entre docente e comunidade e favorecendo o processo de ensino aprendizagem.
um mediador possibilitando uma formação pessoal do indivíduo, dando a ele o direito de entender e intervir na sociedade na qual está inserido, o direito de tornar-se cidadão, de maneira assistemática e esporádica.
um acolhedor das diferenças e as considerar no processo de ensino aprendizagem, reconhecendo que cada estudante aprende de uma forma diferente, desenvolvendo um contexto próprio para ser reconhecido apenas como indivíduo alfabetizado.
um mediador do processo de construção do conhecimento, utilizando um método que seja ativo, dialógico, crítico e criticista, possibilitando uma interação maior entre docente e discente e favorecendo o processo de ensino aprendizagem.
um mediador, facilitador e articulador do conhecimento, aquele que detém toda a informação e saber. Ele deve atuar como um pesquisador, que provoca o aluno a ser também curioso e descobrir a partir de seus próprios questionamentos, que deverá negociar os conhecimentos adquiridos e apoiar os estudantes e juntos sintetizarem o conhecimento compartilhado.
De acordo com o exposto e considerando a etnomatemática para o repensar o fazer pedagógico dos professores, analise as afirmativas a seguir.
I. A Educação Matemática, neste enfoque, contempla o saber oriundo do cotidiano, a qual acredita que está imbuído de saberes e fazeres próprios da cultura.
II. Tem a pretensão de substituir a matemática acadêmica, que é absolutamente inútil na sociedade, considerando a educação multicultural como uma possibilidade a qual valoriza e reconhece como legítimo o saber matemático oriundo das diversas culturas.
III. Tem como objetivo conectar a realidade com a matemática, promovendo o estudo a partir do mundo vivido/concreto para a análise dos conteúdos abstratos e a resolução de problemas que propiciam a compreensão e a constituição de saberes e alternativas para o contexto.
IV. O termo etnomatemática foi constituído por Ubiratan D.Ambrósio. Para compor a palavra etnomatemática, utilizam‐se as raízes tica, matema e etn” para significar que há várias maneiras, técnicas, habilidades (ticas) de explicar, de entender, de lidar e de conviver com (matema) distintos contextos naturais e socioeconômicos da realidade (etnos).
Estão corretas as afirmativas
I, II e III
I, II e IV
II e IV
II, III e IV
I, III e IV
A Etnomatemática surgiu na década de 1970, com base em críticas sociais acerca do ensino tradicional da Matemática, como a análise das práticas matemáticas em seus diferentes contextos culturais. Mais adiante, o conceito passou a designar as diferenças culturais nas diferentes formas de conhecimento, uma junção dos termos techné, mátema e etno, esta proposta educacional defende que a Matemática deve ser explicada e entendida dentro de um contexto cultural próprio, tendo Ubiratan DAmbrósio como precursor e idealizador no Brasil.
Sendo assim, analise as alternativas a seguir e assinale a alternativa que indica as que estão corretas:
I- A Etnomatemática é uma proposta educacional que aborda as relações interculturais da Matemática, em que a disciplina deve ser compreendida para além da constituição social, mas também como construção histórica e política.
II- Muitas vezes, a influência recíproca entre duas ou mais culturas não é levada em consideração na historiografia da Matemática, o que traz implicações na educação. Existe a enorme tendência de se trabalhar a Matemática da cultura predominante, sem a influência do ambiente cultural do aluno.
III- A Etnomatemática defende que se enfatizem as ações pedagógicas construídas dentro do contexto sociocultural dos educandos, levando-se em consideração os distintos grupos culturais. Assim sendo, são enaltecidos os conceitos matemáticos informais desenvolvidos pelos alunos através de seus conhecimentos, fora da vivência escolar.
IV- Etnomatemática valoriza as diferenças e defende que toda construção do conhecimento matemático, está intimamente relacionado com a tradição, sociedade e cultura de cada povo. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
V- O ensino da matemática na perspectiva Etnomatemática contempla as experiências cotidianas e, por isso, enriquece a relação entre teoria e prática, onde a linguagem matemática está presente nas mais diversas atividades humanas, como nas artes, arquitetura, música, dança, esporte, engenharia etc., e faz parte do contexto da sociedade na qual o indivíduo está inserido, estando, assim, relacionada ao social e cultural.
A respeito dessas asserções, assinale a alternativa correta:
Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:

( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:

I, II e III
I, II e IV
II e IV
II, III e IV
I, III e IV
A Etnomatemática surgiu na década de 1970, com base em críticas sociais acerca do ensino tradicional da Matemática, como a análise das práticas matemáticas em seus diferentes contextos culturais. Mais adiante, o conceito passou a designar as diferenças culturais nas diferentes formas de conhecimento, uma junção dos termos techné, mátema e etno, esta proposta educacional defende que a Matemática deve ser explicada e entendida dentro de um contexto cultural próprio, tendo Ubiratan DAmbrósio como precursor e idealizador no Brasil.
Sendo assim, analise as alternativas a seguir e assinale a alternativa que indica as que estão corretas:
I- A Etnomatemática é uma proposta educacional que aborda as relações interculturais da Matemática, em que a disciplina deve ser compreendida para além da constituição social, mas também como construção histórica e política.
II- Muitas vezes, a influência recíproca entre duas ou mais culturas não é levada em consideração na historiografia da Matemática, o que traz implicações na educação. Existe a enorme tendência de se trabalhar a Matemática da cultura predominante, sem a influência do ambiente cultural do aluno.
III- A Etnomatemática defende que se enfatizem as ações pedagógicas construídas dentro do contexto sociocultural dos educandos, levando-se em consideração os distintos grupos culturais. Assim sendo, são enaltecidos os conceitos matemáticos informais desenvolvidos pelos alunos através de seus conhecimentos, fora da vivência escolar.
IV- Etnomatemática valoriza as diferenças e defende que toda construção do conhecimento matemático, está intimamente relacionado com a tradição, sociedade e cultura de cada povo. Os povos em suas diferentes culturas possuem inúmeras maneiras de trabalharem o conceito matemático e todos os conhecimentos produzidos pelos grupos sociais são válidos.
V- O ensino da matemática na perspectiva Etnomatemática contempla as experiências cotidianas e, por isso, enriquece a relação entre teoria e prática, onde a linguagem matemática está presente nas mais diversas atividades humanas, como nas artes, arquitetura, música, dança, esporte, engenharia etc., e faz parte do contexto da sociedade na qual o indivíduo está inserido, estando, assim, relacionada ao social e cultural.
A respeito dessas asserções, assinale a alternativa correta:
Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:

( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:

Apenas a II está incorreta.
Apenas a IV está incorreta.
Apenas a III está incorreta.
Todas estão corretas.
Estão corretas I, II e V apenas.
Os assuntos monômios e polinômios, geralmente, não são bem compreendidos pelos alunos devido a uma certa aridez com que o assunto é tratado. No entanto, podemos utilizar um recurso didático para facilitar a compreensão das operações algébricas, até duas variáveis, através da manipulação de figuras geométricas coloridas. Este recurso didático chama-se algeplan. Como você já aprendeu a utilizá-lo, encontre o produto que corresponde à área hachurada da figura e desenvolva o produto aplicando a propriedade distributiva da multiplicação para obter o produto notável, sendo assim, assinale a alternativa que corresponde respectivamente:

( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:


( a + b)2 e a2+ 2ab + b2
a2 -2ab + b2 e (a - b)2
(a + b) . (a - b) e a² - b²
(a - b)2 e a2 -2ab + b2
a² - b² e (a - b) . (a - b)
Analisando a figura, podemos dizer que o polinômio que representa à área do quadrado 1, e identificado por qual das expressões algébricas a seguir:

