CÁLCULO I
Seja dada a função %7D) , determine a sua SEGUNDA derivada, e em seguida, assinale a alternativa CORRETA.
, determine a sua SEGUNDA derivada, e em seguida, assinale a alternativa CORRETA.
%7D%2B%7B2%7D.%7B%5Csec%7B%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D%5Cright)%7D%7D%7D)
%7D)
%7D%2B%7B2%7D%7B%5Ccos%7B%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D%5Cright)%7D%7D%7D)
![y'=-4x^2.sen(x^2+3)[1+x^2+3]](http://sga.uniube.br/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7By%7D'%3D-%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D.%7Bs%7D%7Be%7D%7Bn%7D%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D%5Cright)%7D%7B%5Cleft%5B%7B1%7D%2B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D%5Cright%5D%7D)
%7D%7D%7D)
Dada a função  , determine o valor de
, determine o valor de 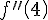 , e em seguida, assinale a alternativa CORRETA.
, e em seguida, assinale a alternativa CORRETA.



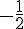
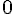
Realize a operação de derivação sucessiva para a função 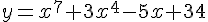 até a ordem
até a ordem 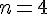 e, em seguida, assinale a alternativa CORRETA.
e, em seguida, assinale a alternativa CORRETA.
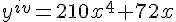
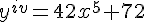
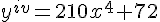
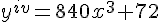
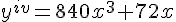
Dada a função 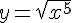 assinale a alternativa CORRETA que representa a sua primeira derivada.
assinale a alternativa CORRETA que representa a sua primeira derivada.








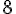

Dada a função  encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.
encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.





Leia o trecho, a seguir, extraído do livro: SILVA, L. M. et al. Cálculo diferencial e integral, volume 1 – São Paulo: Pearson Prentice Hall, 2010, página 97:
"Esse processo de derivação pode continuar enquanto as funções sejam deriváveis e, dessa forma, podemos encontrar a derivada enésima  da função
da função %7D%7D%7D) ." (SILVA, 2010, p.97).
." (SILVA, 2010, p.97).
O trecho anterior, refere-se a conclusão da definição de derivações sucessivas.
Seja dada a função 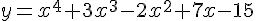 , ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
, ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
Para 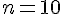 não existe derivada, pois a função não é derivável.
não existe derivada, pois a função não é derivável.
para 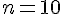 , todas as derivadas sucessivas são iguais a
, todas as derivadas sucessivas são iguais a 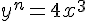
Para 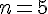 a função é constante e igual a
a função é constante e igual a 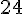
A derivada sucessiva 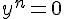 será válida para quaisquer derivadas sucessivas de
será válida para quaisquer derivadas sucessivas de 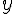 quando
quando 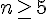 .
.
Para 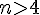 não existem derivadas sucessivas para esta função.
não existem derivadas sucessivas para esta função.
Seja dada a função %7D%7D%7D) tal que
tal que  a alternativa CORRETA que representa a primeira derivada
a alternativa CORRETA que representa a primeira derivada %7D) será dada EXATAMENTE por:
será dada EXATAMENTE por:
Dada a função  , determine o valor de
, determine o valor de 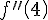 , e em seguida, assinale a alternativa CORRETA.
, e em seguida, assinale a alternativa CORRETA.



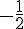
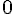
Realize a operação de derivação sucessiva para a função 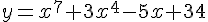 até a ordem
até a ordem 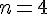 e, em seguida, assinale a alternativa CORRETA.
e, em seguida, assinale a alternativa CORRETA.
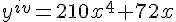
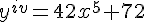
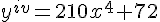
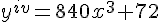
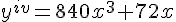
Dada a função 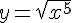 assinale a alternativa CORRETA que representa a sua primeira derivada.
assinale a alternativa CORRETA que representa a sua primeira derivada.







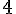

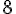

Dada a função  encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.
encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.





Leia o trecho, a seguir, extraído do livro: SILVA, L. M. et al. Cálculo diferencial e integral, volume 1 – São Paulo: Pearson Prentice Hall, 2010, página 97:
"Esse processo de derivação pode continuar enquanto as funções sejam deriváveis e, dessa forma, podemos encontrar a derivada enésima  da função
da função %7D%7D%7D) ." (SILVA, 2010, p.97).
." (SILVA, 2010, p.97).
O trecho anterior, refere-se a conclusão da definição de derivações sucessivas.
Seja dada a função 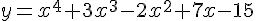 , ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
, ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
Para 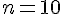 não existe derivada, pois a função não é derivável.
não existe derivada, pois a função não é derivável.
para 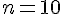 , todas as derivadas sucessivas são iguais a
, todas as derivadas sucessivas são iguais a 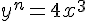
Para 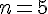 a função é constante e igual a
a função é constante e igual a 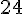
A derivada sucessiva 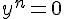 será válida para quaisquer derivadas sucessivas de
será válida para quaisquer derivadas sucessivas de 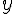 quando
quando 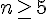 .
.
Para 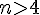 não existem derivadas sucessivas para esta função.
não existem derivadas sucessivas para esta função.
Seja dada a função %7D%7D%7D) tal que
tal que  a alternativa CORRETA que representa a primeira derivada
a alternativa CORRETA que representa a primeira derivada %7D) será dada EXATAMENTE por:
será dada EXATAMENTE por:
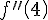 , e em seguida, assinale a alternativa CORRETA.
, e em seguida, assinale a alternativa CORRETA.
Realize a operação de derivação sucessiva para a função 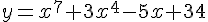 até a ordem
até a ordem 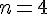 e, em seguida, assinale a alternativa CORRETA.
e, em seguida, assinale a alternativa CORRETA.
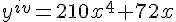
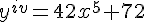
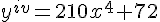
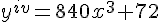
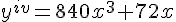
Dada a função 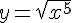 assinale a alternativa CORRETA que representa a sua primeira derivada.
assinale a alternativa CORRETA que representa a sua primeira derivada.








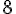

Dada a função  encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.
encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.





Leia o trecho, a seguir, extraído do livro: SILVA, L. M. et al. Cálculo diferencial e integral, volume 1 – São Paulo: Pearson Prentice Hall, 2010, página 97:
"Esse processo de derivação pode continuar enquanto as funções sejam deriváveis e, dessa forma, podemos encontrar a derivada enésima  da função
da função %7D%7D%7D) ." (SILVA, 2010, p.97).
." (SILVA, 2010, p.97).
O trecho anterior, refere-se a conclusão da definição de derivações sucessivas.
Seja dada a função 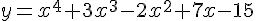 , ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
, ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
Para 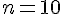 não existe derivada, pois a função não é derivável.
não existe derivada, pois a função não é derivável.
para 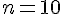 , todas as derivadas sucessivas são iguais a
, todas as derivadas sucessivas são iguais a 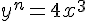
Para 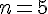 a função é constante e igual a
a função é constante e igual a 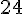
A derivada sucessiva 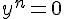 será válida para quaisquer derivadas sucessivas de
será válida para quaisquer derivadas sucessivas de 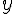 quando
quando 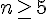 .
.
Para 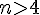 não existem derivadas sucessivas para esta função.
não existem derivadas sucessivas para esta função.
Seja dada a função %7D%7D%7D) tal que
tal que  a alternativa CORRETA que representa a primeira derivada
a alternativa CORRETA que representa a primeira derivada %7D) será dada EXATAMENTE por:
será dada EXATAMENTE por:
Dada a função 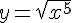 assinale a alternativa CORRETA que representa a sua primeira derivada.
assinale a alternativa CORRETA que representa a sua primeira derivada.







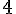

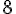

Dada a função  encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.
encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.





Leia o trecho, a seguir, extraído do livro: SILVA, L. M. et al. Cálculo diferencial e integral, volume 1 – São Paulo: Pearson Prentice Hall, 2010, página 97:
"Esse processo de derivação pode continuar enquanto as funções sejam deriváveis e, dessa forma, podemos encontrar a derivada enésima  da função
da função %7D%7D%7D) ." (SILVA, 2010, p.97).
." (SILVA, 2010, p.97).
O trecho anterior, refere-se a conclusão da definição de derivações sucessivas.
Seja dada a função 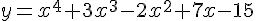 , ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
, ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
Para 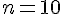 não existe derivada, pois a função não é derivável.
não existe derivada, pois a função não é derivável.
para 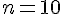 , todas as derivadas sucessivas são iguais a
, todas as derivadas sucessivas são iguais a 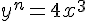
Para 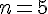 a função é constante e igual a
a função é constante e igual a 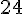
A derivada sucessiva 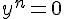 será válida para quaisquer derivadas sucessivas de
será válida para quaisquer derivadas sucessivas de 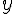 quando
quando 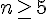 .
.
Para 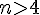 não existem derivadas sucessivas para esta função.
não existem derivadas sucessivas para esta função.
Seja dada a função %7D%7D%7D) tal que
tal que  a alternativa CORRETA que representa a primeira derivada
a alternativa CORRETA que representa a primeira derivada %7D) será dada EXATAMENTE por:
será dada EXATAMENTE por:


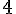

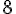

Dada a função  encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.
encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.





Leia o trecho, a seguir, extraído do livro: SILVA, L. M. et al. Cálculo diferencial e integral, volume 1 – São Paulo: Pearson Prentice Hall, 2010, página 97:
"Esse processo de derivação pode continuar enquanto as funções sejam deriváveis e, dessa forma, podemos encontrar a derivada enésima  da função
da função %7D%7D%7D) ." (SILVA, 2010, p.97).
." (SILVA, 2010, p.97).
O trecho anterior, refere-se a conclusão da definição de derivações sucessivas.
Seja dada a função 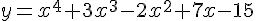 , ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
, ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
Para 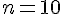 não existe derivada, pois a função não é derivável.
não existe derivada, pois a função não é derivável.
para 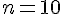 , todas as derivadas sucessivas são iguais a
, todas as derivadas sucessivas são iguais a 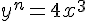
Para 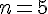 a função é constante e igual a
a função é constante e igual a 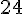
A derivada sucessiva 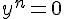 será válida para quaisquer derivadas sucessivas de
será válida para quaisquer derivadas sucessivas de 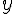 quando
quando 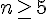 .
.
Para 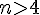 não existem derivadas sucessivas para esta função.
não existem derivadas sucessivas para esta função.
Seja dada a função %7D%7D%7D) tal que
tal que  a alternativa CORRETA que representa a primeira derivada
a alternativa CORRETA que representa a primeira derivada %7D) será dada EXATAMENTE por:
será dada EXATAMENTE por:

Dada a função  encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.
encontre a primeira derivada, e em seguida assinale a alternativa CORRETA.





Leia o trecho, a seguir, extraído do livro: SILVA, L. M. et al. Cálculo diferencial e integral, volume 1 – São Paulo: Pearson Prentice Hall, 2010, página 97:
"Esse processo de derivação pode continuar enquanto as funções sejam deriváveis e, dessa forma, podemos encontrar a derivada enésima  da função
da função %7D%7D%7D) ." (SILVA, 2010, p.97).
." (SILVA, 2010, p.97).
O trecho anterior, refere-se a conclusão da definição de derivações sucessivas.
Seja dada a função 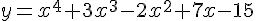 , ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
, ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
Para 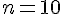 não existe derivada, pois a função não é derivável.
não existe derivada, pois a função não é derivável.
para 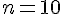 , todas as derivadas sucessivas são iguais a
, todas as derivadas sucessivas são iguais a 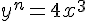
Para 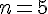 a função é constante e igual a
a função é constante e igual a 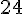
A derivada sucessiva 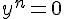 será válida para quaisquer derivadas sucessivas de
será válida para quaisquer derivadas sucessivas de 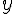 quando
quando 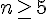 .
.
Para 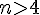 não existem derivadas sucessivas para esta função.
não existem derivadas sucessivas para esta função.
Seja dada a função %7D%7D%7D) tal que
tal que  a alternativa CORRETA que representa a primeira derivada
a alternativa CORRETA que representa a primeira derivada %7D) será dada EXATAMENTE por:
será dada EXATAMENTE por:
Leia o trecho, a seguir, extraído do livro: SILVA, L. M. et al. Cálculo diferencial e integral, volume 1 – São Paulo: Pearson Prentice Hall, 2010, página 97:
"Esse processo de derivação pode continuar enquanto as funções sejam deriváveis e, dessa forma, podemos encontrar a derivada enésima  da função
da função %7D%7D%7D) ." (SILVA, 2010, p.97).
." (SILVA, 2010, p.97).
O trecho anterior, refere-se a conclusão da definição de derivações sucessivas.
Seja dada a função 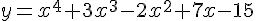 , ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
, ao realizar a operação de derivação sucessiva até a ordem 10 (n=10), para esta função, é possível afirmar que. Assinale a alternativa CORRETA.
Para 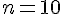 não existe derivada, pois a função não é derivável.
não existe derivada, pois a função não é derivável.
para 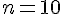 , todas as derivadas sucessivas são iguais a
, todas as derivadas sucessivas são iguais a 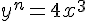
Para 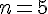 a função é constante e igual a
a função é constante e igual a 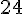
A derivada sucessiva 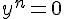 será válida para quaisquer derivadas sucessivas de
será válida para quaisquer derivadas sucessivas de 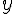 quando
quando 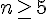 .
.
Para 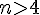 não existem derivadas sucessivas para esta função.
não existem derivadas sucessivas para esta função.
Seja dada a função %7D%7D%7D) tal que
tal que  a alternativa CORRETA que representa a primeira derivada
a alternativa CORRETA que representa a primeira derivada %7D) será dada EXATAMENTE por:
será dada EXATAMENTE por:
Para não existe derivada, pois a função não é derivável.
para , todas as derivadas sucessivas são iguais a
Para a função é constante e igual a
A derivada sucessiva será válida para quaisquer derivadas sucessivas de
quando
.
Para não existem derivadas sucessivas para esta função.
