TEORIA DOS NÚMEROS II
Sabendo que Z é o resultado da operação, (5-2i) -(2-3i) , então o valor do conjugado de Z é igual a:
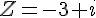
`Z= 7-3i`
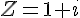
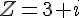
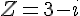
A origem histórica da necessidade de criação dos números irracionais está intimamente ligada com fatos de natureza geométrica e de natureza aritmética. Sendo assim leia as afirmativas a seguir:
I. Toda dízima não-periódica é um número irracional
II. Toda dízima é um número irracional.
III. Toda dízima periódica é um número racional.
IV. Todo número que pode ser escrito sob a forma decimal é real.
V. Números reais são somente aqueles que podem ser representados pela razão entre dois números inteiros
E correto que se afirma em
Apenas I, III e IV
Apenas I, III e V
Apenas II, III e IV
Apenas I, II, e III
Apenas I, II e V
Sr. Jorge fez uma aposta com seu colega, que conseguiria revestir o muro da sua escola em três dias. Revestiu no primeiro dia 1/4 e no segundo dia 1/3 muro. A parte que resta a pintar no terceiro dia corresponde a:
5/12
2/7
5/7
3/4
7/12
Leia as afirmativas a seguir:
I.O conjunto dos números inteiros relativos é infinito.
II. O conjunto dos números racionais é contínuo.
III.Todo número decimal é racional.
IV. Todo número racional é um decimal exato ou periódico.
V.O conjunto dos números inteiros está contido no conjunto dos números racionais
E correto que se afirma em
Apenas I, III , IV e V
Apenas I, II e V
Apenas II, III e IV
Apenas I, IV e V
Apenas I, II , IV e V
Determinar o módulo, o argumento e a formula trigonométrica do seguinte número complexo 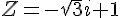 , são respectivamente iguais a:
, são respectivamente iguais a:
2, 320°, z=2(cos 320° - i sen 320°)
2, 300°, z=2(cos 300° +i sen 300°)
3, 300°, z=3(cos 300° +i sen 300°)
 , 320°, z=
, 320°, z= (cos 320° +i sen 320°)
(cos 320° +i sen 320°)
2, 225°, z=2(cos 225° +i sen 225°)
Analisando a representação gráfica do número complexo a seguir, determine o seu módulo:
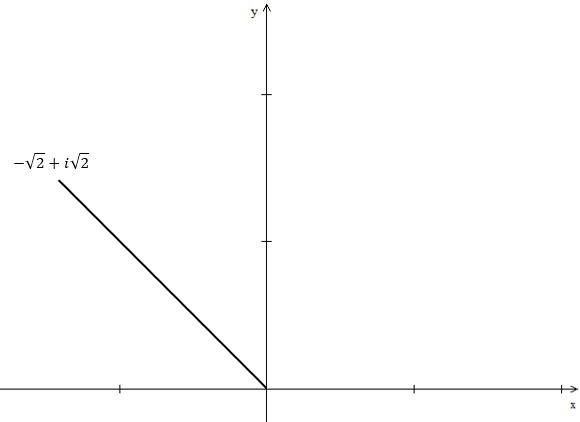
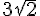

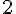
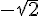

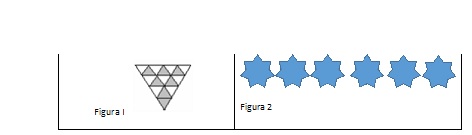
Analisando as representações a seguir (figura 1 e figura 2), marque a alternativa que apresenta a concepção de fração está presente em cada uma das situações, respectivamente:
Nenhuma das anteriores
A relação parte-todo em um todo discreto e a relação parte-todo em um todo contínuo
Ambas a relação parte-todo em um todo discreto
Ambas a relação parte-todo, em um todo contínuo
A relação parte-todo em todo contínuo e a relação parte-todo em um todo discreto;
Na casa de Bruno, o gasto diário do consumo de energia, corresponde a 2/5 da sua despesa total. Com a troca dos novos tipos de lâmpadas LED, que são mais econômicas, seu consumo passou a ser de 1/4 da sua despesa. Logo, a fração que representa a economia com essa troca foi de:
3/20
1/10
1/8
3/2
3/5
Dado o número complexo na forma álgebrica  , então z10 é igual a:
, então z10 é igual a:
`Z= 7-3i`
A origem histórica da necessidade de criação dos números irracionais está intimamente ligada com fatos de natureza geométrica e de natureza aritmética. Sendo assim leia as afirmativas a seguir:
I. Toda dízima não-periódica é um número irracional
II. Toda dízima é um número irracional.
III. Toda dízima periódica é um número racional.
IV. Todo número que pode ser escrito sob a forma decimal é real.
V. Números reais são somente aqueles que podem ser representados pela razão entre dois números inteiros
E correto que se afirma em
Apenas I, III e IV
Apenas I, III e V
Apenas II, III e IV
Apenas I, II, e III
Apenas I, II e V
Sr. Jorge fez uma aposta com seu colega, que conseguiria revestir o muro da sua escola em três dias. Revestiu no primeiro dia 1/4 e no segundo dia 1/3 muro. A parte que resta a pintar no terceiro dia corresponde a:
5/12
2/7
5/7
3/4
7/12
Leia as afirmativas a seguir:
I.O conjunto dos números inteiros relativos é infinito.
II. O conjunto dos números racionais é contínuo.
III.Todo número decimal é racional.
IV. Todo número racional é um decimal exato ou periódico.
V.O conjunto dos números inteiros está contido no conjunto dos números racionais
E correto que se afirma em
Apenas I, III , IV e V
Apenas I, II e V
Apenas II, III e IV
Apenas I, IV e V
Apenas I, II , IV e V
Determinar o módulo, o argumento e a formula trigonométrica do seguinte número complexo 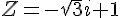 , são respectivamente iguais a:
, são respectivamente iguais a:
2, 320°, z=2(cos 320° - i sen 320°)
2, 300°, z=2(cos 300° +i sen 300°)
3, 300°, z=3(cos 300° +i sen 300°)
 , 320°, z=
, 320°, z= (cos 320° +i sen 320°)
(cos 320° +i sen 320°)
2, 225°, z=2(cos 225° +i sen 225°)
Analisando a representação gráfica do número complexo a seguir, determine o seu módulo:

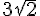

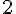
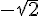

Analisando as representações a seguir (figura 1 e figura 2), marque a alternativa que apresenta a concepção de fração está presente em cada uma das situações, respectivamente:

Nenhuma das anteriores
A relação parte-todo em um todo discreto e a relação parte-todo em um todo contínuo
Ambas a relação parte-todo em um todo discreto
Ambas a relação parte-todo, em um todo contínuo
A relação parte-todo em todo contínuo e a relação parte-todo em um todo discreto;
Na casa de Bruno, o gasto diário do consumo de energia, corresponde a 2/5 da sua despesa total. Com a troca dos novos tipos de lâmpadas LED, que são mais econômicas, seu consumo passou a ser de 1/4 da sua despesa. Logo, a fração que representa a economia com essa troca foi de:
3/20
1/10
1/8
3/2
3/5
Dado o número complexo na forma álgebrica  , então z10 é igual a:
, então z10 é igual a:
Apenas I, III e IV
Apenas I, III e V
Apenas II, III e IV
Apenas I, II, e III
Apenas I, II e V
Sr. Jorge fez uma aposta com seu colega, que conseguiria revestir o muro da sua escola em três dias. Revestiu no primeiro dia 1/4 e no segundo dia 1/3 muro. A parte que resta a pintar no terceiro dia corresponde a:
5/12
2/7
5/7
3/4
7/12
Leia as afirmativas a seguir:
I.O conjunto dos números inteiros relativos é infinito.
II. O conjunto dos números racionais é contínuo.
III.Todo número decimal é racional.
IV. Todo número racional é um decimal exato ou periódico.
V.O conjunto dos números inteiros está contido no conjunto dos números racionais
E correto que se afirma em
Apenas I, III , IV e V
Apenas I, II e V
Apenas II, III e IV
Apenas I, IV e V
Apenas I, II , IV e V
Determinar o módulo, o argumento e a formula trigonométrica do seguinte número complexo 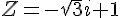 , são respectivamente iguais a:
, são respectivamente iguais a:
2, 320°, z=2(cos 320° - i sen 320°)
2, 300°, z=2(cos 300° +i sen 300°)
3, 300°, z=3(cos 300° +i sen 300°)
 , 320°, z=
, 320°, z= (cos 320° +i sen 320°)
(cos 320° +i sen 320°)
2, 225°, z=2(cos 225° +i sen 225°)
Analisando a representação gráfica do número complexo a seguir, determine o seu módulo:

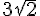

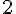
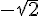

Analisando as representações a seguir (figura 1 e figura 2), marque a alternativa que apresenta a concepção de fração está presente em cada uma das situações, respectivamente:

Nenhuma das anteriores
A relação parte-todo em um todo discreto e a relação parte-todo em um todo contínuo
Ambas a relação parte-todo em um todo discreto
Ambas a relação parte-todo, em um todo contínuo
A relação parte-todo em todo contínuo e a relação parte-todo em um todo discreto;
Na casa de Bruno, o gasto diário do consumo de energia, corresponde a 2/5 da sua despesa total. Com a troca dos novos tipos de lâmpadas LED, que são mais econômicas, seu consumo passou a ser de 1/4 da sua despesa. Logo, a fração que representa a economia com essa troca foi de:
3/20
1/10
1/8
3/2
3/5
Dado o número complexo na forma álgebrica  , então z10 é igual a:
, então z10 é igual a:
5/12
2/7
5/7
3/4
7/12
Leia as afirmativas a seguir:
I.O conjunto dos números inteiros relativos é infinito.
II. O conjunto dos números racionais é contínuo.
III.Todo número decimal é racional.
IV. Todo número racional é um decimal exato ou periódico.
V.O conjunto dos números inteiros está contido no conjunto dos números racionais
E correto que se afirma em
Apenas I, III , IV e V
Apenas I, II e V
Apenas II, III e IV
Apenas I, IV e V
Apenas I, II , IV e V
Determinar o módulo, o argumento e a formula trigonométrica do seguinte número complexo 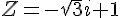 , são respectivamente iguais a:
, são respectivamente iguais a:
2, 320°, z=2(cos 320° - i sen 320°)
2, 300°, z=2(cos 300° +i sen 300°)
3, 300°, z=3(cos 300° +i sen 300°)
 , 320°, z=
, 320°, z= (cos 320° +i sen 320°)
(cos 320° +i sen 320°)
2, 225°, z=2(cos 225° +i sen 225°)
Analisando a representação gráfica do número complexo a seguir, determine o seu módulo:

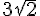

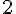
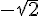

Analisando as representações a seguir (figura 1 e figura 2), marque a alternativa que apresenta a concepção de fração está presente em cada uma das situações, respectivamente:

Nenhuma das anteriores
A relação parte-todo em um todo discreto e a relação parte-todo em um todo contínuo
Ambas a relação parte-todo em um todo discreto
Ambas a relação parte-todo, em um todo contínuo
A relação parte-todo em todo contínuo e a relação parte-todo em um todo discreto;
Na casa de Bruno, o gasto diário do consumo de energia, corresponde a 2/5 da sua despesa total. Com a troca dos novos tipos de lâmpadas LED, que são mais econômicas, seu consumo passou a ser de 1/4 da sua despesa. Logo, a fração que representa a economia com essa troca foi de:
3/20
1/10
1/8
3/2
3/5
Dado o número complexo na forma álgebrica  , então z10 é igual a:
, então z10 é igual a:
Apenas I, III , IV e V
Apenas I, II e V
Apenas II, III e IV
Apenas I, IV e V
Apenas I, II , IV e V
Determinar o módulo, o argumento e a formula trigonométrica do seguinte número complexo 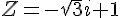 , são respectivamente iguais a:
, são respectivamente iguais a:
2, 320°, z=2(cos 320° - i sen 320°)
2, 300°, z=2(cos 300° +i sen 300°)
3, 300°, z=3(cos 300° +i sen 300°)
 , 320°, z=
, 320°, z= (cos 320° +i sen 320°)
(cos 320° +i sen 320°)
2, 225°, z=2(cos 225° +i sen 225°)
Analisando a representação gráfica do número complexo a seguir, determine o seu módulo:

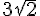

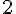
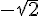

Analisando as representações a seguir (figura 1 e figura 2), marque a alternativa que apresenta a concepção de fração está presente em cada uma das situações, respectivamente:

Nenhuma das anteriores
A relação parte-todo em um todo discreto e a relação parte-todo em um todo contínuo
Ambas a relação parte-todo em um todo discreto
Ambas a relação parte-todo, em um todo contínuo
A relação parte-todo em todo contínuo e a relação parte-todo em um todo discreto;
Na casa de Bruno, o gasto diário do consumo de energia, corresponde a 2/5 da sua despesa total. Com a troca dos novos tipos de lâmpadas LED, que são mais econômicas, seu consumo passou a ser de 1/4 da sua despesa. Logo, a fração que representa a economia com essa troca foi de:
3/20
1/10
1/8
3/2
3/5
Dado o número complexo na forma álgebrica  , então z10 é igual a:
, então z10 é igual a:
2, 320°, z=2(cos 320° - i sen 320°)
2, 300°, z=2(cos 300° +i sen 300°)
3, 300°, z=3(cos 300° +i sen 300°)
2, 225°, z=2(cos 225° +i sen 225°)
Analisando a representação gráfica do número complexo a seguir, determine o seu módulo:

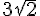

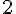
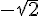

Analisando as representações a seguir (figura 1 e figura 2), marque a alternativa que apresenta a concepção de fração está presente em cada uma das situações, respectivamente:

Nenhuma das anteriores
A relação parte-todo em um todo discreto e a relação parte-todo em um todo contínuo
Ambas a relação parte-todo em um todo discreto
Ambas a relação parte-todo, em um todo contínuo
A relação parte-todo em todo contínuo e a relação parte-todo em um todo discreto;
Na casa de Bruno, o gasto diário do consumo de energia, corresponde a 2/5 da sua despesa total. Com a troca dos novos tipos de lâmpadas LED, que são mais econômicas, seu consumo passou a ser de 1/4 da sua despesa. Logo, a fração que representa a economia com essa troca foi de:
3/20
1/10
1/8
3/2
3/5
Dado o número complexo na forma álgebrica  , então z10 é igual a:
, então z10 é igual a:

Analisando as representações a seguir (figura 1 e figura 2), marque a alternativa que apresenta a concepção de fração está presente em cada uma das situações, respectivamente:

Nenhuma das anteriores
A relação parte-todo em um todo discreto e a relação parte-todo em um todo contínuo
Ambas a relação parte-todo em um todo discreto
Ambas a relação parte-todo, em um todo contínuo
A relação parte-todo em todo contínuo e a relação parte-todo em um todo discreto;
Na casa de Bruno, o gasto diário do consumo de energia, corresponde a 2/5 da sua despesa total. Com a troca dos novos tipos de lâmpadas LED, que são mais econômicas, seu consumo passou a ser de 1/4 da sua despesa. Logo, a fração que representa a economia com essa troca foi de:
3/20
1/10
1/8
3/2
3/5
Dado o número complexo na forma álgebrica  , então z10 é igual a:
, então z10 é igual a:

Nenhuma das anteriores
A relação parte-todo em um todo discreto e a relação parte-todo em um todo contínuo
Ambas a relação parte-todo em um todo discreto
Ambas a relação parte-todo, em um todo contínuo
A relação parte-todo em todo contínuo e a relação parte-todo em um todo discreto;
Na casa de Bruno, o gasto diário do consumo de energia, corresponde a 2/5 da sua despesa total. Com a troca dos novos tipos de lâmpadas LED, que são mais econômicas, seu consumo passou a ser de 1/4 da sua despesa. Logo, a fração que representa a economia com essa troca foi de:
3/20
1/10
1/8
3/2
3/5
Dado o número complexo na forma álgebrica  , então z10 é igual a:
, então z10 é igual a:
3/20
1/10
1/8
3/2
3/5