SISTEMAS DE CONTROLE II
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Considere a seguinte função de transferência:
%7D%7D%7D%7B%7B%7BU%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B3%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B3%7D%7Bs%7D%2B%7B2%7D%7D%7D)
Qual a representação no espaço de estados desse sistema na forma canônica controlável.
Considere a seguinte função de transferência:
Qual a representação no espaço de estados desse sistema na forma canônica observável.
Considere a seguinte função de transferência:
%7D%7D%7D%7B%7B%7BU%7D%7B%5Cleft(%7Bs%7D%5Cright)%7D%7D%7D%3D%5Cfrac%7B%7B%7Bs%7D%2B%7B6%7D%7D%7D%7B%7B%7B%7Bs%7D%7D%5E%7B%7B2%7D%7D%2B%7B5%7D%7Bs%7D%2B%7B6%7D%7D%7D "(Y(s))/(U(s))=(s+6)/(s^2+5s+6)")
Qual a representação no espaço de estados desse sistema na forma canônica controlável.
Coma base na figura abaixo responda. O sistema é:
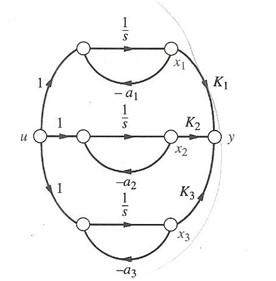
Observável
Não controlável
Não observável
Controlável
Suportável
Um sistema a ser controlado apresenta uma resposta ao degrau, em malha aberta, com um erro de aproximadamente 2%, para menos, em regime permanente, sem sobrepasso (overshoot) nem oscilações.
Para tentar zerar esse erro em regime permanente, qual deveria ser o controlador para fazer uma realimentação?
Proporcional-integral (PI).
Puramente derivativo.
Proporcional (P).
Proporcional-integral-derivativo (PID).
Proporcional-derivativo (PD).
Quais são as três técnicas básicas de projeto de sistemas de controle por realimentação?
Lugar das raízes, Resposta em período e Alimentação de estados.
Alimentação das raízes, Pergunta em frequência e Realimentação de estados.
Projeto das raízes, Resposta em frequência e Realimentação de sistemas.
Lugar das raízes, Resposta em frequência e Realimentação de estados.
Realimentação de sistemas, Pergunta em frequência e Projeto das raízes.
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
%7D%3D%5Cfrac%7B%7B%7B0%7D%2C%7B368%7D%7Bz%7D%2B%7B0%7D%2C%7B265%7D%7D%7D%7B%7B%7B%7Bz%7D%7D%5E%7B%7B2%7D%7D-%7B1%7D%2C%7B368%7D%7Bz%7D%2B%7B0%7D%2C%7B368%7D%7D%7D "G(z)=(0,368z+0,265)/(z^2-1,368z+0,368)")
Considere a seguinte função de transferência:
Qual a representação no espaço de estados desse sistema na forma canônica controlável.
Considere a seguinte função de transferência:
Qual a representação no espaço de estados desse sistema na forma canônica observável.
Considere a seguinte função de transferência:
Qual a representação no espaço de estados desse sistema na forma canônica controlável.
Coma base na figura abaixo responda. O sistema é:
Observável
Não controlável
Não observável
Controlável
Suportável
Um sistema a ser controlado apresenta uma resposta ao degrau, em malha aberta, com um erro de aproximadamente 2%, para menos, em regime permanente, sem sobrepasso (overshoot) nem oscilações.
Para tentar zerar esse erro em regime permanente, qual deveria ser o controlador para fazer uma realimentação?
Proporcional-integral (PI).
Puramente derivativo.
Proporcional (P).
Proporcional-integral-derivativo (PID).
Proporcional-derivativo (PD).
Quais são as três técnicas básicas de projeto de sistemas de controle por realimentação?
Lugar das raízes, Resposta em período e Alimentação de estados.
Alimentação das raízes, Pergunta em frequência e Realimentação de estados.
Projeto das raízes, Resposta em frequência e Realimentação de sistemas.
Lugar das raízes, Resposta em frequência e Realimentação de estados.
Realimentação de sistemas, Pergunta em frequência e Projeto das raízes.
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
Considere a seguinte função de transferência:
Qual a representação no espaço de estados desse sistema na forma canônica observável.
Considere a seguinte função de transferência:
Qual a representação no espaço de estados desse sistema na forma canônica controlável.
Coma base na figura abaixo responda. O sistema é:
Observável
Não controlável
Não observável
Controlável
Suportável
Um sistema a ser controlado apresenta uma resposta ao degrau, em malha aberta, com um erro de aproximadamente 2%, para menos, em regime permanente, sem sobrepasso (overshoot) nem oscilações.
Para tentar zerar esse erro em regime permanente, qual deveria ser o controlador para fazer uma realimentação?
Proporcional-integral (PI).
Puramente derivativo.
Proporcional (P).
Proporcional-integral-derivativo (PID).
Proporcional-derivativo (PD).
Quais são as três técnicas básicas de projeto de sistemas de controle por realimentação?
Lugar das raízes, Resposta em período e Alimentação de estados.
Alimentação das raízes, Pergunta em frequência e Realimentação de estados.
Projeto das raízes, Resposta em frequência e Realimentação de sistemas.
Lugar das raízes, Resposta em frequência e Realimentação de estados.
Realimentação de sistemas, Pergunta em frequência e Projeto das raízes.
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
Considere a seguinte função de transferência:
Qual a representação no espaço de estados desse sistema na forma canônica controlável.
Coma base na figura abaixo responda. O sistema é:
Observável
Não controlável
Não observável
Controlável
Suportável
Um sistema a ser controlado apresenta uma resposta ao degrau, em malha aberta, com um erro de aproximadamente 2%, para menos, em regime permanente, sem sobrepasso (overshoot) nem oscilações.
Para tentar zerar esse erro em regime permanente, qual deveria ser o controlador para fazer uma realimentação?
Proporcional-integral (PI).
Puramente derivativo.
Proporcional (P).
Proporcional-integral-derivativo (PID).
Proporcional-derivativo (PD).
Quais são as três técnicas básicas de projeto de sistemas de controle por realimentação?
Lugar das raízes, Resposta em período e Alimentação de estados.
Alimentação das raízes, Pergunta em frequência e Realimentação de estados.
Projeto das raízes, Resposta em frequência e Realimentação de sistemas.
Lugar das raízes, Resposta em frequência e Realimentação de estados.
Realimentação de sistemas, Pergunta em frequência e Projeto das raízes.
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
Coma base na figura abaixo responda. O sistema é:
Observável
Não controlável
Não observável
Controlável
Suportável
Um sistema a ser controlado apresenta uma resposta ao degrau, em malha aberta, com um erro de aproximadamente 2%, para menos, em regime permanente, sem sobrepasso (overshoot) nem oscilações.
Para tentar zerar esse erro em regime permanente, qual deveria ser o controlador para fazer uma realimentação?
Proporcional-integral (PI).
Puramente derivativo.
Proporcional (P).
Proporcional-integral-derivativo (PID).
Proporcional-derivativo (PD).
Quais são as três técnicas básicas de projeto de sistemas de controle por realimentação?
Lugar das raízes, Resposta em período e Alimentação de estados.
Alimentação das raízes, Pergunta em frequência e Realimentação de estados.
Projeto das raízes, Resposta em frequência e Realimentação de sistemas.
Lugar das raízes, Resposta em frequência e Realimentação de estados.
Realimentação de sistemas, Pergunta em frequência e Projeto das raízes.
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
Observável
Não controlável
Não observável
Controlável
Suportável
Um sistema a ser controlado apresenta uma resposta ao degrau, em malha aberta, com um erro de aproximadamente 2%, para menos, em regime permanente, sem sobrepasso (overshoot) nem oscilações.
Para tentar zerar esse erro em regime permanente, qual deveria ser o controlador para fazer uma realimentação?
Proporcional-integral (PI).
Puramente derivativo.
Proporcional (P).
Proporcional-integral-derivativo (PID).
Proporcional-derivativo (PD).
Quais são as três técnicas básicas de projeto de sistemas de controle por realimentação?
Lugar das raízes, Resposta em período e Alimentação de estados.
Alimentação das raízes, Pergunta em frequência e Realimentação de estados.
Projeto das raízes, Resposta em frequência e Realimentação de sistemas.
Lugar das raízes, Resposta em frequência e Realimentação de estados.
Realimentação de sistemas, Pergunta em frequência e Projeto das raízes.
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
Proporcional-integral (PI).
Puramente derivativo.
Proporcional (P).
Proporcional-integral-derivativo (PID).
Proporcional-derivativo (PD).
Quais são as três técnicas básicas de projeto de sistemas de controle por realimentação?
Lugar das raízes, Resposta em período e Alimentação de estados.
Alimentação das raízes, Pergunta em frequência e Realimentação de estados.
Projeto das raízes, Resposta em frequência e Realimentação de sistemas.
Lugar das raízes, Resposta em frequência e Realimentação de estados.
Realimentação de sistemas, Pergunta em frequência e Projeto das raízes.
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
Lugar das raízes, Resposta em período e Alimentação de estados.
Alimentação das raízes, Pergunta em frequência e Realimentação de estados.
Projeto das raízes, Resposta em frequência e Realimentação de sistemas.
Lugar das raízes, Resposta em frequência e Realimentação de estados.
Realimentação de sistemas, Pergunta em frequência e Projeto das raízes.
Considere o seguinte sistema:
Qual a representação no espaço de estados do sistema na forma canônica diagonal.
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
Sobre independência linear é correto afirmar que:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3
Projetar um controlador Dead-Beat para o seguinte sistema:
Quando algum elemento contido nele é gerado por uma combinação linear dos outros.
Se na equação h2y2 = k1y1 + k3y3 tivermos algum yi = 0, então, yi pode ser escrito como combinação linear das outras variáveis, para todo ki = 0.
Se a combinação S = 0 e todos os ki = 0 e nenhum yi = 0, dizemos que as variáveis não serão independentes.
Quando um conjunto de varáveis não pode ser escrito como uma combinação linear das outras.
Quando uma das equações a seguir pode ser escrita como combinação linear da outra elas são linearmente independentes.
y1, y2 e y3 = 4y1 + 5y3