QUÍMICA ANALÍTICA INSTRUMENTAL
A técnica de adição de padrão é muito conveniente nos mais variados tipos de análise, pois em determinadas situações ela acaba eliminando a interferência de certas espécies sobre a dosagem em questão, muito aplicada à análise de medicamentos já prontos para serem encaminhados ao mercado. A cetamina é um anestésico comercialmente vendido com nome de KETALAR®. O KETALAR® geralmente é encontrado numa concentração contendo o equivalente a 50 mg de cetamina por mL de medicamento. Para determinação de cetamina no KETALAR® na indústria farmacêutica pode-se usar a técnica de adição de padrão. Um lote deste medicamento foi analisado a partir da curva analítica apresentada a seguir.

A partir do gráfico acima, pergunta-se:
Qual a concentração, em mg/mL, de cetamina na solução amostra?
0,05
77,3
2,45
4,57
9,63
Em uma análise cromatográfica de placa, na fase móvel as substâncias que queremos isolar são arrastadas por um solvente, que pode ser líquido ou gasoso. Imagine que você queira identificar um composto "polar", através dessa análise, qual dos compostos abaixo apresentaria maior polaridade, para atuar como fase móvel desse experimento?
Hexano
Metanol
Metano
Tetracloreto de metila
Alumina
Uma análise cromatográfica, utilizando ácido acético como fase móvel e hexano como fase estacionária, apresentou Rf igual a 0,0027. Baseado nessa informação, qual das substâncias abaixo estava sendo analisada:
Antraceno
Clorometano
Amônia
Água
Cloreto de sódio
Após um acidente, um lago foi contaminado com Cromo hexavalente, colocando em risco o bioma existente. Para determinar o nível de contaminação, retirou uma amostra da água do lago e analisou em um fotômetro de chama, obtendo um valor de emissão de 79,5. Uma amostra contendo 3,5 x 10-5g/mL de Cr (VI) foi analisada no mesmo fotômetro, resultando em uma leitura de 27,8. Com base nesses dados, qual alternativa contém a concentração correta de Cr (VI) no lago?
2,8 x 10-7 g/mL
8,3 x 10-4 g/mL
3,5 x 10-2 g/mL
1,0 x 10-4 g/mL
4,5 x 10-3 g/mL
Para determinar o mercúrio (Hg) contido em uma amostra de água contaminada, utilizou-se a curva analítica Abs = 0,0603 CHg2+ + 0,0079, onde a concentração de mercúrio é dada em mg/L. A amostra de água apresentou uma absorbância de 0,522. Qual a concentração de mercúrio na amostra?
10,9 mg/L
65,6 mg/L
8,52 mg/L
87,0 mg/L
0,6 mg/L
Encontre a absorbância e a transmitância (%) de uma solução 0,00240 M de uma substância com coeficiente de absortividade molar de 313 M-1 cm-1, numa célula com 2,00 cm de caminho óptico.
2,457 e 0,32%
0,456 e 0,04%
0,876 e 6,5%
0,3678 e 40,5%
1,5024 e 3,14%
Uma solução de um dado composto apresenta uma absortividade molar de 8,5x103 M-1 cm-1 em 450 nm. Calcule a concentração do composto em uma amostra apresenta absorbância de 0,300 quando medidas em 450 nm numa cubeta de 2 cm.
5,45 x 10-6 mol/L
5,72 x 10-5 mol/L
6,51 x 10-4 mol/L
1,76 x 10-5 mol/L
3,52 x 10-5 mol/L
Em um laboratório foram feitos testes cromatográficos com as substâncias A,B e C. Após as análises, utilizando uma fase estacionária apolar, obteve-se o cromatograma abaixo. Qual das alternativas contém a correlação certa entre os compostos e os picos no cromatograma.
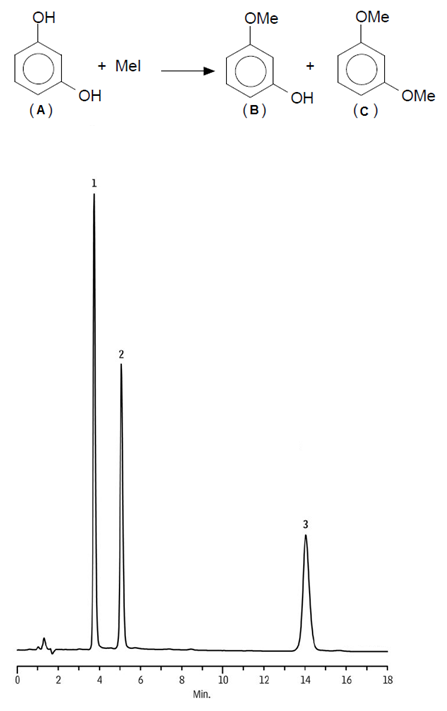
A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.
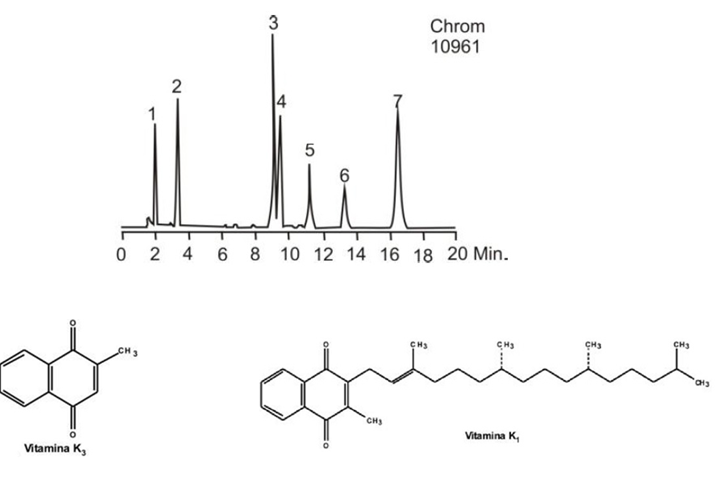
A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:
0,05
77,3
2,45
4,57
9,63
Em uma análise cromatográfica de placa, na fase móvel as substâncias que queremos isolar são arrastadas por um solvente, que pode ser líquido ou gasoso. Imagine que você queira identificar um composto "polar", através dessa análise, qual dos compostos abaixo apresentaria maior polaridade, para atuar como fase móvel desse experimento?
Hexano
Metanol
Metano
Tetracloreto de metila
Alumina
Uma análise cromatográfica, utilizando ácido acético como fase móvel e hexano como fase estacionária, apresentou Rf igual a 0,0027. Baseado nessa informação, qual das substâncias abaixo estava sendo analisada:
Antraceno
Clorometano
Amônia
Água
Cloreto de sódio
Após um acidente, um lago foi contaminado com Cromo hexavalente, colocando em risco o bioma existente. Para determinar o nível de contaminação, retirou uma amostra da água do lago e analisou em um fotômetro de chama, obtendo um valor de emissão de 79,5. Uma amostra contendo 3,5 x 10-5g/mL de Cr (VI) foi analisada no mesmo fotômetro, resultando em uma leitura de 27,8. Com base nesses dados, qual alternativa contém a concentração correta de Cr (VI) no lago?
2,8 x 10-7 g/mL
8,3 x 10-4 g/mL
3,5 x 10-2 g/mL
1,0 x 10-4 g/mL
4,5 x 10-3 g/mL
Para determinar o mercúrio (Hg) contido em uma amostra de água contaminada, utilizou-se a curva analítica Abs = 0,0603 CHg2+ + 0,0079, onde a concentração de mercúrio é dada em mg/L. A amostra de água apresentou uma absorbância de 0,522. Qual a concentração de mercúrio na amostra?
10,9 mg/L
65,6 mg/L
8,52 mg/L
87,0 mg/L
0,6 mg/L
Encontre a absorbância e a transmitância (%) de uma solução 0,00240 M de uma substância com coeficiente de absortividade molar de 313 M-1 cm-1, numa célula com 2,00 cm de caminho óptico.
2,457 e 0,32%
0,456 e 0,04%
0,876 e 6,5%
0,3678 e 40,5%
1,5024 e 3,14%
Uma solução de um dado composto apresenta uma absortividade molar de 8,5x103 M-1 cm-1 em 450 nm. Calcule a concentração do composto em uma amostra apresenta absorbância de 0,300 quando medidas em 450 nm numa cubeta de 2 cm.
5,45 x 10-6 mol/L
5,72 x 10-5 mol/L
6,51 x 10-4 mol/L
1,76 x 10-5 mol/L
3,52 x 10-5 mol/L
Em um laboratório foram feitos testes cromatográficos com as substâncias A,B e C. Após as análises, utilizando uma fase estacionária apolar, obteve-se o cromatograma abaixo. Qual das alternativas contém a correlação certa entre os compostos e os picos no cromatograma.

A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:
Hexano
Metanol
Metano
Tetracloreto de metila
Alumina
Uma análise cromatográfica, utilizando ácido acético como fase móvel e hexano como fase estacionária, apresentou Rf igual a 0,0027. Baseado nessa informação, qual das substâncias abaixo estava sendo analisada:
Antraceno
Clorometano
Amônia
Água
Cloreto de sódio
Após um acidente, um lago foi contaminado com Cromo hexavalente, colocando em risco o bioma existente. Para determinar o nível de contaminação, retirou uma amostra da água do lago e analisou em um fotômetro de chama, obtendo um valor de emissão de 79,5. Uma amostra contendo 3,5 x 10-5g/mL de Cr (VI) foi analisada no mesmo fotômetro, resultando em uma leitura de 27,8. Com base nesses dados, qual alternativa contém a concentração correta de Cr (VI) no lago?
2,8 x 10-7 g/mL
8,3 x 10-4 g/mL
3,5 x 10-2 g/mL
1,0 x 10-4 g/mL
4,5 x 10-3 g/mL
Para determinar o mercúrio (Hg) contido em uma amostra de água contaminada, utilizou-se a curva analítica Abs = 0,0603 CHg2+ + 0,0079, onde a concentração de mercúrio é dada em mg/L. A amostra de água apresentou uma absorbância de 0,522. Qual a concentração de mercúrio na amostra?
10,9 mg/L
65,6 mg/L
8,52 mg/L
87,0 mg/L
0,6 mg/L
Encontre a absorbância e a transmitância (%) de uma solução 0,00240 M de uma substância com coeficiente de absortividade molar de 313 M-1 cm-1, numa célula com 2,00 cm de caminho óptico.
2,457 e 0,32%
0,456 e 0,04%
0,876 e 6,5%
0,3678 e 40,5%
1,5024 e 3,14%
Uma solução de um dado composto apresenta uma absortividade molar de 8,5x103 M-1 cm-1 em 450 nm. Calcule a concentração do composto em uma amostra apresenta absorbância de 0,300 quando medidas em 450 nm numa cubeta de 2 cm.
5,45 x 10-6 mol/L
5,72 x 10-5 mol/L
6,51 x 10-4 mol/L
1,76 x 10-5 mol/L
3,52 x 10-5 mol/L
Em um laboratório foram feitos testes cromatográficos com as substâncias A,B e C. Após as análises, utilizando uma fase estacionária apolar, obteve-se o cromatograma abaixo. Qual das alternativas contém a correlação certa entre os compostos e os picos no cromatograma.

A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:
Antraceno
Clorometano
Amônia
Água
Cloreto de sódio
Após um acidente, um lago foi contaminado com Cromo hexavalente, colocando em risco o bioma existente. Para determinar o nível de contaminação, retirou uma amostra da água do lago e analisou em um fotômetro de chama, obtendo um valor de emissão de 79,5. Uma amostra contendo 3,5 x 10-5g/mL de Cr (VI) foi analisada no mesmo fotômetro, resultando em uma leitura de 27,8. Com base nesses dados, qual alternativa contém a concentração correta de Cr (VI) no lago?
2,8 x 10-7 g/mL
8,3 x 10-4 g/mL
3,5 x 10-2 g/mL
1,0 x 10-4 g/mL
4,5 x 10-3 g/mL
Para determinar o mercúrio (Hg) contido em uma amostra de água contaminada, utilizou-se a curva analítica Abs = 0,0603 CHg2+ + 0,0079, onde a concentração de mercúrio é dada em mg/L. A amostra de água apresentou uma absorbância de 0,522. Qual a concentração de mercúrio na amostra?
10,9 mg/L
65,6 mg/L
8,52 mg/L
87,0 mg/L
0,6 mg/L
Encontre a absorbância e a transmitância (%) de uma solução 0,00240 M de uma substância com coeficiente de absortividade molar de 313 M-1 cm-1, numa célula com 2,00 cm de caminho óptico.
2,457 e 0,32%
0,456 e 0,04%
0,876 e 6,5%
0,3678 e 40,5%
1,5024 e 3,14%
Uma solução de um dado composto apresenta uma absortividade molar de 8,5x103 M-1 cm-1 em 450 nm. Calcule a concentração do composto em uma amostra apresenta absorbância de 0,300 quando medidas em 450 nm numa cubeta de 2 cm.
5,45 x 10-6 mol/L
5,72 x 10-5 mol/L
6,51 x 10-4 mol/L
1,76 x 10-5 mol/L
3,52 x 10-5 mol/L
Em um laboratório foram feitos testes cromatográficos com as substâncias A,B e C. Após as análises, utilizando uma fase estacionária apolar, obteve-se o cromatograma abaixo. Qual das alternativas contém a correlação certa entre os compostos e os picos no cromatograma.

A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:
2,8 x 10-7 g/mL
8,3 x 10-4 g/mL
3,5 x 10-2 g/mL
1,0 x 10-4 g/mL
4,5 x 10-3 g/mL
Para determinar o mercúrio (Hg) contido em uma amostra de água contaminada, utilizou-se a curva analítica Abs = 0,0603 CHg2+ + 0,0079, onde a concentração de mercúrio é dada em mg/L. A amostra de água apresentou uma absorbância de 0,522. Qual a concentração de mercúrio na amostra?
10,9 mg/L
65,6 mg/L
8,52 mg/L
87,0 mg/L
0,6 mg/L
Encontre a absorbância e a transmitância (%) de uma solução 0,00240 M de uma substância com coeficiente de absortividade molar de 313 M-1 cm-1, numa célula com 2,00 cm de caminho óptico.
2,457 e 0,32%
0,456 e 0,04%
0,876 e 6,5%
0,3678 e 40,5%
1,5024 e 3,14%
Uma solução de um dado composto apresenta uma absortividade molar de 8,5x103 M-1 cm-1 em 450 nm. Calcule a concentração do composto em uma amostra apresenta absorbância de 0,300 quando medidas em 450 nm numa cubeta de 2 cm.
5,45 x 10-6 mol/L
5,72 x 10-5 mol/L
6,51 x 10-4 mol/L
1,76 x 10-5 mol/L
3,52 x 10-5 mol/L
Em um laboratório foram feitos testes cromatográficos com as substâncias A,B e C. Após as análises, utilizando uma fase estacionária apolar, obteve-se o cromatograma abaixo. Qual das alternativas contém a correlação certa entre os compostos e os picos no cromatograma.

A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:
10,9 mg/L
65,6 mg/L
8,52 mg/L
87,0 mg/L
0,6 mg/L
Encontre a absorbância e a transmitância (%) de uma solução 0,00240 M de uma substância com coeficiente de absortividade molar de 313 M-1 cm-1, numa célula com 2,00 cm de caminho óptico.
2,457 e 0,32%
0,456 e 0,04%
0,876 e 6,5%
0,3678 e 40,5%
1,5024 e 3,14%
Uma solução de um dado composto apresenta uma absortividade molar de 8,5x103 M-1 cm-1 em 450 nm. Calcule a concentração do composto em uma amostra apresenta absorbância de 0,300 quando medidas em 450 nm numa cubeta de 2 cm.
5,45 x 10-6 mol/L
5,72 x 10-5 mol/L
6,51 x 10-4 mol/L
1,76 x 10-5 mol/L
3,52 x 10-5 mol/L
Em um laboratório foram feitos testes cromatográficos com as substâncias A,B e C. Após as análises, utilizando uma fase estacionária apolar, obteve-se o cromatograma abaixo. Qual das alternativas contém a correlação certa entre os compostos e os picos no cromatograma.

A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:
2,457 e 0,32%
0,456 e 0,04%
0,876 e 6,5%
0,3678 e 40,5%
1,5024 e 3,14%
Uma solução de um dado composto apresenta uma absortividade molar de 8,5x103 M-1 cm-1 em 450 nm. Calcule a concentração do composto em uma amostra apresenta absorbância de 0,300 quando medidas em 450 nm numa cubeta de 2 cm.
5,45 x 10-6 mol/L
5,72 x 10-5 mol/L
6,51 x 10-4 mol/L
1,76 x 10-5 mol/L
3,52 x 10-5 mol/L
Em um laboratório foram feitos testes cromatográficos com as substâncias A,B e C. Após as análises, utilizando uma fase estacionária apolar, obteve-se o cromatograma abaixo. Qual das alternativas contém a correlação certa entre os compostos e os picos no cromatograma.

A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:
5,45 x 10-6 mol/L
5,72 x 10-5 mol/L
6,51 x 10-4 mol/L
1,76 x 10-5 mol/L
3,52 x 10-5 mol/L
Em um laboratório foram feitos testes cromatográficos com as substâncias A,B e C. Após as análises, utilizando uma fase estacionária apolar, obteve-se o cromatograma abaixo. Qual das alternativas contém a correlação certa entre os compostos e os picos no cromatograma.

A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:

A=2; B=2 e C=1
A=3; B=1 e C=2
A=3; B=2 e C=1
A=1; B=2 e C=3
A=1; B=3 e C=2
A seguir, é apresentado um cromatograma em que se realizou a separação de várias vitaminas. Analisando o cromatograma, estrutura dos compostos, e sabendo que a ordem de eluição é aquela colocada para os componentes, por que a substancia 1 (K3), embora similar em parte à substancia 7 (K1), apresenta tempo de eluição tão diferente? Dados: Coluna: C18; Fase móvel: Metanol:Acetonitrila (40:60); Detector: UV em 280 nm; Componentes: K3, A, D2, D3, E, Acetato de vitamina E e K1.

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:

A substância 7 (K1) apresenta uma longa cadeia lateral de hidrocarboneto, tornando-a mais apolar.
A fase estacionária é muito polar.
A coluna deve estar contaminada com terpenoides.
A substância 1 (K3) é mais apolar.
O operador do equipamento errou na montagem da rampa de aquecimento.
Correlacione as colunas:
1 - Injetor ( ) Compõe a fase móvel na CG
2 - Gás de arraste ( ) promove a separação cromatográfica
3 - Manômetro ( ) vaporiza a amostra
4 - Coluna ( ) Promove o aquecimento do detector
5 - Forno ( ) Envia sinal elétrico para o amplificador
6 - Detector ( ) Controla a vazão do gás
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é:
1 - Injetor ( ) Compõe a fase móvel na CG
A sequência que relaciona corretamente a coluna da esquerda com a coluna da direita é: