PRÉ-CÁLCULO I

3
2
4
7
6
A semelhança de triângulos é a comparação entre lados proporcionais e ângulos congruentes de triângulos a fim de saber se eles são semelhantes.
Quando comparamos duas figuras geralmente queremos saber quais as semelhanças existentes entre elas. Algumas vezes elas são iguais, algumas vezes são apenas parecidas e também existem os casos em que as figuras comparadas são completamente diferentes.
“O teorema fundamental da semelhança de triângulos afirma que toda reta paralela a um dos lados do triângulo que intercepta os outros dois lados determina um segundo triângulo semelhante ao primeiro.”
No triângulo ABC, o segmento DE é paralelo ao lado BC. Sabe-se também que AB = 8 cm, AC = 10 cm e AD = 2 cm. Determinando o comprimento dos segmentos AE e EC, teremos:

AE = 7,5 cm e EC = 3,5 cm.
AE = 2,5 cm e EC = 7,5 cm.
AE = 2,5 cm e EC = 10 cm.
AE = 7,5 cm e EC = 2,5 cm.
AE = 2,5 cm e EC = 12,5 cm.
Os triângulos (I) e (II), abaixo, são semelhantes.
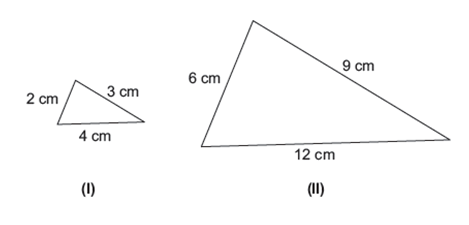
Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
y = 9x
y = 3x
y = 3x + 3
y = 2x
y = x
Equações são expressões matemáticas algébricas que possuem uma ou mais incógnitas, sempre apresentadas com o sinal de igualdade. Equação modular se enquadra neste conceito geral, mas no caso das modulares, as incógnitas se encontram dentro do módulo; dessa forma, devemos respeitar as condições do módulo de um número:

Considere a equação modular a seguir e determinando o seu conjunto solução, teremos:

S = {1, 6}, apenas.
S = {- 6, - 1 , 1, 6}
S = {- 3, - 1 , 1, 3}
S = {- 6, - 1 , 0, 1, 6}
S = {- 6, - 1}, apenas.
A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:

29
75
30
25
45
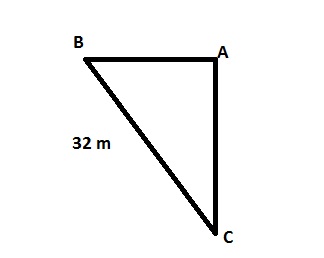
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
22,56 metros
5,52 metros
15,6 metros
10,56 metros
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,004x +100
f(x) = - 0,032x
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = 0,032x -100
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
3
2
4
7
6
A semelhança de triângulos é a comparação entre lados proporcionais e ângulos congruentes de triângulos a fim de saber se eles são semelhantes.
Quando comparamos duas figuras geralmente queremos saber quais as semelhanças existentes entre elas. Algumas vezes elas são iguais, algumas vezes são apenas parecidas e também existem os casos em que as figuras comparadas são completamente diferentes.
“O teorema fundamental da semelhança de triângulos afirma que toda reta paralela a um dos lados do triângulo que intercepta os outros dois lados determina um segundo triângulo semelhante ao primeiro.”
No triângulo ABC, o segmento DE é paralelo ao lado BC. Sabe-se também que AB = 8 cm, AC = 10 cm e AD = 2 cm. Determinando o comprimento dos segmentos AE e EC, teremos:

AE = 7,5 cm e EC = 3,5 cm.
AE = 2,5 cm e EC = 7,5 cm.
AE = 2,5 cm e EC = 10 cm.
AE = 7,5 cm e EC = 2,5 cm.
AE = 2,5 cm e EC = 12,5 cm.
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
y = 9x
y = 3x
y = 3x + 3
y = 2x
y = x
Equações são expressões matemáticas algébricas que possuem uma ou mais incógnitas, sempre apresentadas com o sinal de igualdade. Equação modular se enquadra neste conceito geral, mas no caso das modulares, as incógnitas se encontram dentro do módulo; dessa forma, devemos respeitar as condições do módulo de um número:

Considere a equação modular a seguir e determinando o seu conjunto solução, teremos:

S = {1, 6}, apenas.
S = {- 6, - 1 , 1, 6}
S = {- 3, - 1 , 1, 3}
S = {- 6, - 1 , 0, 1, 6}
S = {- 6, - 1}, apenas.
A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:

29
75
30
25
45
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
22,56 metros
5,52 metros
15,6 metros
10,56 metros
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,004x +100
f(x) = - 0,032x
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = 0,032x -100
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
AE = 7,5 cm e EC = 3,5 cm.
AE = 2,5 cm e EC = 7,5 cm.
AE = 2,5 cm e EC = 10 cm.
AE = 7,5 cm e EC = 2,5 cm.
AE = 2,5 cm e EC = 12,5 cm.
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
y = 9x
y = 3x
y = 3x + 3
y = 2x
y = x
Equações são expressões matemáticas algébricas que possuem uma ou mais incógnitas, sempre apresentadas com o sinal de igualdade. Equação modular se enquadra neste conceito geral, mas no caso das modulares, as incógnitas se encontram dentro do módulo; dessa forma, devemos respeitar as condições do módulo de um número:

Considere a equação modular a seguir e determinando o seu conjunto solução, teremos:

S = {1, 6}, apenas.
S = {- 6, - 1 , 1, 6}
S = {- 3, - 1 , 1, 3}
S = {- 6, - 1 , 0, 1, 6}
S = {- 6, - 1}, apenas.
A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:

29
75
30
25
45
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
22,56 metros
5,52 metros
15,6 metros
10,56 metros
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,004x +100
f(x) = - 0,032x
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = 0,032x -100
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?

y = 9x
y = 3x
y = 3x + 3
y = 2x
y = x
Equações são expressões matemáticas algébricas que possuem uma ou mais incógnitas, sempre apresentadas com o sinal de igualdade. Equação modular se enquadra neste conceito geral, mas no caso das modulares, as incógnitas se encontram dentro do módulo; dessa forma, devemos respeitar as condições do módulo de um número:

Considere a equação modular a seguir e determinando o seu conjunto solução, teremos:

S = {1, 6}, apenas.
S = {- 6, - 1 , 1, 6}
S = {- 3, - 1 , 1, 3}
S = {- 6, - 1 , 0, 1, 6}
S = {- 6, - 1}, apenas.
A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:

29
75
30
25
45
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
22,56 metros
5,52 metros
15,6 metros
10,56 metros
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,004x +100
f(x) = - 0,032x
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = 0,032x -100
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
S = {1, 6}, apenas.
S = {- 6, - 1 , 1, 6}
S = {- 3, - 1 , 1, 3}
S = {- 6, - 1 , 0, 1, 6}
S = {- 6, - 1}, apenas.
A sombra de um prédio, em um terreno plano, em uma determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m. A altura do prédio, em metros, é:

29
75
30
25
45
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
22,56 metros
5,52 metros
15,6 metros
10,56 metros
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,004x +100
f(x) = - 0,032x
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = 0,032x -100
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
29
75
30
25
45
Marcelo quer calcular a altura de uma árvore, sabendo que a distância entre os pontos A e B ele conseguiu medir e ainda o ângulo entre o solo e a direção até o topo da árvore, indicados na figura a seguir
Marcelo utilizou as informações a seguir para calcular corretamente a altura dessa árvore.
sen(α)
cos(α)
tg(α)
0,88
0,46
1,88
A altura encontrada por Marcelo é igual a:
7,36 metros
22,56 metros
5,52 metros
15,6 metros
10,56 metros
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,004x +100
f(x) = - 0,032x
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = 0,032x -100
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
7,36 metros
22,56 metros
5,52 metros
15,6 metros
10,56 metros
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,004x +100
f(x) = - 0,032x
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = 0,032x -100
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?
f(x) = - 0,004x +100
f(x) = - 0,032x
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = 0,032x -100
Os triângulos (I) e (II), abaixo, são semelhantes.

Considere as medidas indicadas na figura, a área do triângulo (I) igual a x, e a área do triângulo (II) igual a y.
Que relação existe entre x e y?