MATEMÁTICA III
Dado 
, se 
então senx é igual a:
-1/2
0
1
1/2
-1
O gráfico a seguir, representa a função:
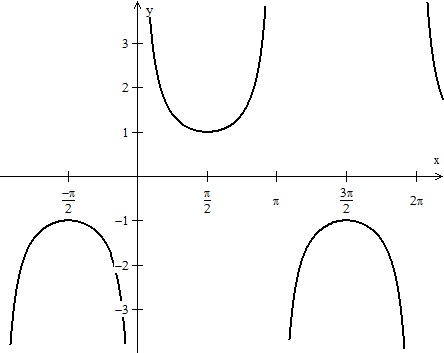
y = sec(x)
y = cossec(x)
y = - cossec(x)
y = 2cossec(x)
y = - sec(x)
Seja %7D%7D%7D%3D%7Bt%7D%7Bg%7B%7Bx%7D%7D%7D "f(x)=tgx")
, os valores de x que assumem o zero da função são dados por:
e 
Um relógio marca 10 horas e 10 minutos. O menor ângulo entre os ponteiros é exatamente:
95°
155°
105°
115°
145°
A rua Professor Zazá e a avenida Nenê de Jesus, ambas retilíneas, cruzam-se conforme um ângulo de 30º. Um posto de gasolina encontra-se na avenida a 600 m do cruzamento e um supermercado situa-se a x metros do posto na rua boca do Jacaré, conforme figura.
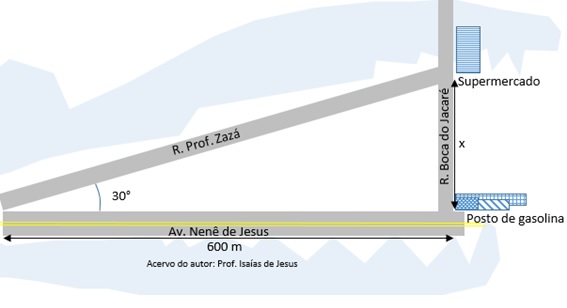
Se a rua boca do Jacaré é perpendicular a Av. Nenê de Jesus podemos afirmar que a distância aproximada entre o posto de gasolina e o supermercado é:
376,49 m.
364,48 m.
346,41 m.
316,41 m.
349,61 m.
Sobre a função 
é correto afirmar:
y=tgx é positivo nos quadrante I e IV e crescente nos quadrantes II e III.
y=tgx é positivo nos quadrante I e III e decrescente em todos quadrantes.
y=tgx é positivo nos quadrante II e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante I e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante II e IV e crescente em todos quadrantes.
Se 
e 
então %7D%7D%7D "cos(a+b)")
é exatamente:
Considere o ciclo a seguir,
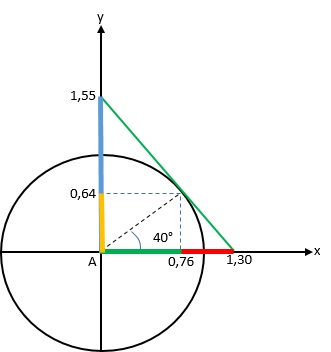
Podemos afirmar que:
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
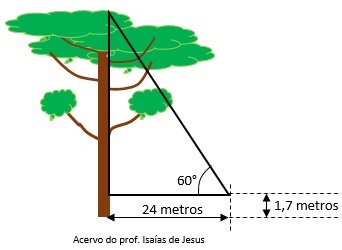
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
-1/2
0
1
1/2
-1
O gráfico a seguir, representa a função:
y = sec(x)
y = cossec(x)
y = - cossec(x)
y = 2cossec(x)
y = - sec(x)
Seja , os valores de x que assumem o zero da função são dados por:
e
Um relógio marca 10 horas e 10 minutos. O menor ângulo entre os ponteiros é exatamente:
95°
155°
105°
115°
145°
A rua Professor Zazá e a avenida Nenê de Jesus, ambas retilíneas, cruzam-se conforme um ângulo de 30º. Um posto de gasolina encontra-se na avenida a 600 m do cruzamento e um supermercado situa-se a x metros do posto na rua boca do Jacaré, conforme figura.
Se a rua boca do Jacaré é perpendicular a Av. Nenê de Jesus podemos afirmar que a distância aproximada entre o posto de gasolina e o supermercado é:
376,49 m.
364,48 m.
346,41 m.
316,41 m.
349,61 m.
Sobre a função é correto afirmar:
y=tgx é positivo nos quadrante I e IV e crescente nos quadrantes II e III.
y=tgx é positivo nos quadrante I e III e decrescente em todos quadrantes.
y=tgx é positivo nos quadrante II e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante I e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante II e IV e crescente em todos quadrantes.
Se e então é exatamente:
Considere o ciclo a seguir,
Podemos afirmar que:
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
y = sec(x)
y = cossec(x)
y = - cossec(x)
y = 2cossec(x)
y = - sec(x)
Seja , os valores de x que assumem o zero da função são dados por:
e
Um relógio marca 10 horas e 10 minutos. O menor ângulo entre os ponteiros é exatamente:
95°
155°
105°
115°
145°
A rua Professor Zazá e a avenida Nenê de Jesus, ambas retilíneas, cruzam-se conforme um ângulo de 30º. Um posto de gasolina encontra-se na avenida a 600 m do cruzamento e um supermercado situa-se a x metros do posto na rua boca do Jacaré, conforme figura.
Se a rua boca do Jacaré é perpendicular a Av. Nenê de Jesus podemos afirmar que a distância aproximada entre o posto de gasolina e o supermercado é:
376,49 m.
364,48 m.
346,41 m.
316,41 m.
349,61 m.
Sobre a função é correto afirmar:
y=tgx é positivo nos quadrante I e IV e crescente nos quadrantes II e III.
y=tgx é positivo nos quadrante I e III e decrescente em todos quadrantes.
y=tgx é positivo nos quadrante II e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante I e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante II e IV e crescente em todos quadrantes.
Se e então é exatamente:
Considere o ciclo a seguir,
Podemos afirmar que:
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
e
Um relógio marca 10 horas e 10 minutos. O menor ângulo entre os ponteiros é exatamente:
95°
155°
105°
115°
145°
A rua Professor Zazá e a avenida Nenê de Jesus, ambas retilíneas, cruzam-se conforme um ângulo de 30º. Um posto de gasolina encontra-se na avenida a 600 m do cruzamento e um supermercado situa-se a x metros do posto na rua boca do Jacaré, conforme figura.
Se a rua boca do Jacaré é perpendicular a Av. Nenê de Jesus podemos afirmar que a distância aproximada entre o posto de gasolina e o supermercado é:
376,49 m.
364,48 m.
346,41 m.
316,41 m.
349,61 m.
Sobre a função é correto afirmar:
y=tgx é positivo nos quadrante I e IV e crescente nos quadrantes II e III.
y=tgx é positivo nos quadrante I e III e decrescente em todos quadrantes.
y=tgx é positivo nos quadrante II e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante I e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante II e IV e crescente em todos quadrantes.
Se e então é exatamente:
Considere o ciclo a seguir,
Podemos afirmar que:
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
95°
155°
105°
115°
145°
A rua Professor Zazá e a avenida Nenê de Jesus, ambas retilíneas, cruzam-se conforme um ângulo de 30º. Um posto de gasolina encontra-se na avenida a 600 m do cruzamento e um supermercado situa-se a x metros do posto na rua boca do Jacaré, conforme figura.
Se a rua boca do Jacaré é perpendicular a Av. Nenê de Jesus podemos afirmar que a distância aproximada entre o posto de gasolina e o supermercado é:
376,49 m.
364,48 m.
346,41 m.
316,41 m.
349,61 m.
Sobre a função é correto afirmar:
y=tgx é positivo nos quadrante I e IV e crescente nos quadrantes II e III.
y=tgx é positivo nos quadrante I e III e decrescente em todos quadrantes.
y=tgx é positivo nos quadrante II e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante I e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante II e IV e crescente em todos quadrantes.
Se e então é exatamente:
Considere o ciclo a seguir,
Podemos afirmar que:
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
376,49 m.
364,48 m.
346,41 m.
316,41 m.
349,61 m.
Sobre a função é correto afirmar:
y=tgx é positivo nos quadrante I e IV e crescente nos quadrantes II e III.
y=tgx é positivo nos quadrante I e III e decrescente em todos quadrantes.
y=tgx é positivo nos quadrante II e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante I e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante II e IV e crescente em todos quadrantes.
Se e então é exatamente:
Considere o ciclo a seguir,
Podemos afirmar que:
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
y=tgx é positivo nos quadrante I e IV e crescente nos quadrantes II e III.
y=tgx é positivo nos quadrante I e III e decrescente em todos quadrantes.
y=tgx é positivo nos quadrante II e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante I e III e crescente em todos quadrantes.
y=tgx é negativo nos quadrante II e IV e crescente em todos quadrantes.
Se e então é exatamente:
Considere o ciclo a seguir,
Podemos afirmar que:
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
Considere o ciclo a seguir,
Podemos afirmar que:
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
1,3 corresponde a cossec40° e 1,55 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a senc40° e 1,55 a cos40°.
Seja f(x) = sen x uma função onde cada ponto do gráfico é da forma (x, senx) em que x representa o comprimento do arco em radianos.
Sobre as características do comportamento da função y = senx, analise as afirmações:
1- O domínio é D(f) = R
2- O conjunto-imagem é im(f) = [-1;1].
3- A função é periódica, de período 2π.
4- O sinal da função é:
positivo no 1º e 3º quadrantes;
negativo no 2º e 4º quadrantes.
5- A função é crescente no 1º e 4º quadrantes e decrescente no 2º e 3º quadrantes.
É correto afirmar:
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.
4 e 5 estão incorretas.
Apenas 4 está incorreta.
Todas as afirmações estão corretas.
Todas estão incorretas.
Apenas 1, 2 e 3 estão corretas.
Pinheiro do Paraná
Nome Científico: Araucaria angustifólia (Araucariaceae)
Características: O Pinheiro do Paraná é uma espécie da classe dos pinheiros (gminospermas) com 20-50 m de altura e tronco retilíneo com 90-180 cm de diâmetro. Suas folhas são aciculadas, coriáceas e glabras. A planta jovem possui forma piramidal e bem diferente da adulta.
Locais de Ocorrência: Ocorre naturalmente em regiões de altitudes acima de 900 m de Minas Gerais, Rio de Janeiro, até o Rio Grande do Sul.
Madeira: Leve, macia e pouco durável.
Disponível em :
< http://www.ibflorestas.org.br/blog/pinheiro-parana/?gclid=CLqL4pH828oCFQsjHwodNskF0Q > acesso em 03/02/2016.
Certa pessoa resolveu a calcular a altura de uma dessas árvores, com a ajuda de um teodolito conseguiu o modelo matemático a seguir:
A altura da árvore é de aproximadamente:
Dados: sen 60° = 0,866 ; cos 60° = 0,5 e tg 60° = 1,732.