MATEMÁTICA II
Duas cidades A e B tem crescimento populacional em milhares segundo as funções:
%7D%3D%7B%5Clog%7D_%7B%7B8%7D%7D%7B%7B%5Cleft(%7B1%7D%2B%7Bt%7D%5Cright)%7D%7D%5E%7B%7B6%7D%7D) e
e %7D%3D%7B%5Clog%7D_%7B%7B2%7D%7D%7B%5Cleft(%7B4%7D%7Bt%7D%2B%7B4%7D%5Cright)%7D) , em que t, é o tempo em anos.
, em que t, é o tempo em anos.
A população de cada uma das cidades A e B no instante t = 7 é igual a:
A(7) = 6 ; B(7) = 7
A(7) = 6 ; B(7) = 5
A(7) = 8 ; B(7) = 5
A(7) = 5 ; B(7) = 6
A(7) = 7 ; B(7) = 6
O Altímetro é um instrumento básico exigido para todas as aeronaves a serem certificadas. Ele mede a pressão atmosférica e apresenta-a como altitude. Esta altitude é denominada nível médio do mar (NMM) ou (MSL Mean Sea Level) uma vez que ela é a referência média do nível da maioria dos oceanos. https://pt.wikipedia.org/wiki/Alt%C3%ADmetro acesso em 09/11/2016>.
Considere que a altitude H acima do nível do mar, em quilômetros, detectada pelo altímetro seja dada pela expressão:%7D%3D%7B22%7D%7B%5Clog%7B%7B%5Cleft(%5Cfrac%7B%7B1%7D%7D%7B%7Bp%7D%7D%5Cright)%7D%7D%7D) .
.
Se num determinado instante a pressão p, é de 0,4 , então a altura H do avião era de
22- 22log2
22(1- log3)
22(1- 2log2)
22(1- log2)
22- 2log2
O valor de 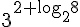 é exatamente:
é exatamente:
81
729
54
27
243
A interseção dos gráficos das funções %7D%7D%7D%3D%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D) e
e %7D%7D%7D%3D%7B1%7D-%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D) esboçadas no mesmo sistema de coordenadas cartesianas, determina um polígono.
esboçadas no mesmo sistema de coordenadas cartesianas, determina um polígono.
A área desse polígono é exatamente:
0,125 u.a
1 u.a
1,5 u.a
0,5 u.a
0,25 u.a
Considerando a equação 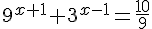 . O valor de
. O valor de 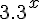 é exatamente:
é exatamente:
1/2
3
1
0
1/3
Resolva em 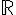 , a equação
, a equação  e marque a opção correta:
e marque a opção correta:
S = {3}
S = { }
S = {2}
S = {1}
S = {8}
Uma função composta pode ser determinada quando é possível comparar duas ou mais grandezas através de uma mesma função. Sejam f e g duas funções de R em R definidas por f(x) = 3x + k e g(x) = -2x + 5, sendo k uma constante real. O valor de k de modo que (fog)(x) = (gof)(x) para todo x, com x ϵ R, é exatamente:
-10/3
-10
-2/3
-3
-1/3
Uma função é par se f(x) = f(-x) e ímpar se f(-x) = -f(x). A seguir são dados os esboços gráficos de função potência do tipo f(x) = xn para n = 1,2,3,4 e 5, respectivamente, em que x é a abscissa e f(x) a ordenada.
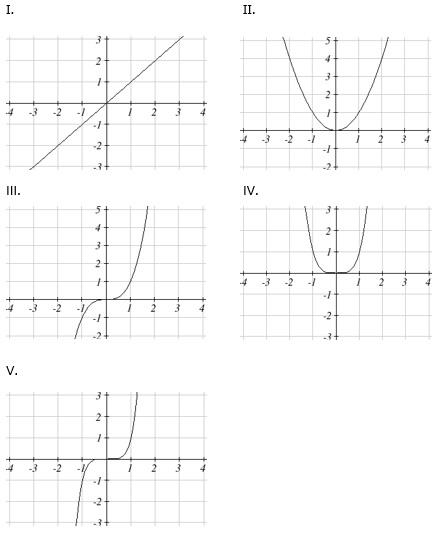
É correto afirmar que:
São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
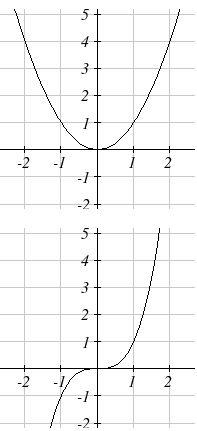
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
A(7) = 6 ; B(7) = 7
A(7) = 6 ; B(7) = 5
A(7) = 8 ; B(7) = 5
A(7) = 5 ; B(7) = 6
A(7) = 7 ; B(7) = 6
O Altímetro é um instrumento básico exigido para todas as aeronaves a serem certificadas. Ele mede a pressão atmosférica e apresenta-a como altitude. Esta altitude é denominada nível médio do mar (NMM) ou (MSL Mean Sea Level) uma vez que ela é a referência média do nível da maioria dos oceanos. https://pt.wikipedia.org/wiki/Alt%C3%ADmetro acesso em 09/11/2016>.
Considere que a altitude H acima do nível do mar, em quilômetros, detectada pelo altímetro seja dada pela expressão:%7D%3D%7B22%7D%7B%5Clog%7B%7B%5Cleft(%5Cfrac%7B%7B1%7D%7D%7B%7Bp%7D%7D%5Cright)%7D%7D%7D) .
.
Se num determinado instante a pressão p, é de 0,4 , então a altura H do avião era de
22- 22log2
22(1- log3)
22(1- 2log2)
22(1- log2)
22- 2log2
O valor de 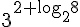 é exatamente:
é exatamente:
81
729
54
27
243
A interseção dos gráficos das funções %7D%7D%7D%3D%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D) e
e %7D%7D%7D%3D%7B1%7D-%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D) esboçadas no mesmo sistema de coordenadas cartesianas, determina um polígono.
esboçadas no mesmo sistema de coordenadas cartesianas, determina um polígono.
A área desse polígono é exatamente:
0,125 u.a
1 u.a
1,5 u.a
0,5 u.a
0,25 u.a
Considerando a equação 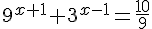 . O valor de
. O valor de 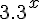 é exatamente:
é exatamente:
1/2
3
1
0
1/3
Resolva em 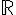 , a equação
, a equação  e marque a opção correta:
e marque a opção correta:
S = {3}
S = { }
S = {2}
S = {1}
S = {8}
Uma função composta pode ser determinada quando é possível comparar duas ou mais grandezas através de uma mesma função. Sejam f e g duas funções de R em R definidas por f(x) = 3x + k e g(x) = -2x + 5, sendo k uma constante real. O valor de k de modo que (fog)(x) = (gof)(x) para todo x, com x ϵ R, é exatamente:
-10/3
-10
-2/3
-3
-1/3
Uma função é par se f(x) = f(-x) e ímpar se f(-x) = -f(x). A seguir são dados os esboços gráficos de função potência do tipo f(x) = xn para n = 1,2,3,4 e 5, respectivamente, em que x é a abscissa e f(x) a ordenada.

É correto afirmar que:
São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
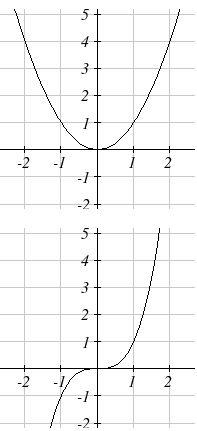
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
22- 22log2
22(1- log3)
22(1- 2log2)
22(1- log2)
22- 2log2
O valor de 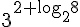 é exatamente:
é exatamente:
81
729
54
27
243
A interseção dos gráficos das funções %7D%7D%7D%3D%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D) e
e %7D%7D%7D%3D%7B1%7D-%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D) esboçadas no mesmo sistema de coordenadas cartesianas, determina um polígono.
esboçadas no mesmo sistema de coordenadas cartesianas, determina um polígono.
A área desse polígono é exatamente:
0,125 u.a
1 u.a
1,5 u.a
0,5 u.a
0,25 u.a
Considerando a equação 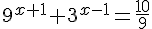 . O valor de
. O valor de 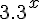 é exatamente:
é exatamente:
1/2
3
1
0
1/3
Resolva em 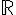 , a equação
, a equação  e marque a opção correta:
e marque a opção correta:
S = {3}
S = { }
S = {2}
S = {1}
S = {8}
Uma função composta pode ser determinada quando é possível comparar duas ou mais grandezas através de uma mesma função. Sejam f e g duas funções de R em R definidas por f(x) = 3x + k e g(x) = -2x + 5, sendo k uma constante real. O valor de k de modo que (fog)(x) = (gof)(x) para todo x, com x ϵ R, é exatamente:
-10/3
-10
-2/3
-3
-1/3
Uma função é par se f(x) = f(-x) e ímpar se f(-x) = -f(x). A seguir são dados os esboços gráficos de função potência do tipo f(x) = xn para n = 1,2,3,4 e 5, respectivamente, em que x é a abscissa e f(x) a ordenada.

É correto afirmar que:
São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
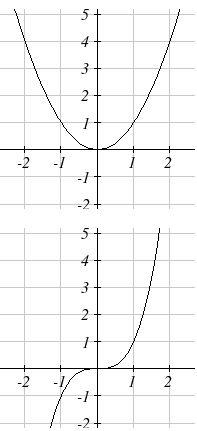
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
81
729
54
27
243
A interseção dos gráficos das funções %7D%7D%7D%3D%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D) e
e %7D%7D%7D%3D%7B1%7D-%7B%5Cleft%7C%7Bx%7D%5Cright%7C%7D) esboçadas no mesmo sistema de coordenadas cartesianas, determina um polígono.
esboçadas no mesmo sistema de coordenadas cartesianas, determina um polígono.
A área desse polígono é exatamente:
0,125 u.a
1 u.a
1,5 u.a
0,5 u.a
0,25 u.a
Considerando a equação 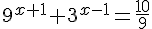 . O valor de
. O valor de 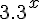 é exatamente:
é exatamente:
1/2
3
1
0
1/3
Resolva em 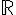 , a equação
, a equação  e marque a opção correta:
e marque a opção correta:
S = {3}
S = { }
S = {2}
S = {1}
S = {8}
Uma função composta pode ser determinada quando é possível comparar duas ou mais grandezas através de uma mesma função. Sejam f e g duas funções de R em R definidas por f(x) = 3x + k e g(x) = -2x + 5, sendo k uma constante real. O valor de k de modo que (fog)(x) = (gof)(x) para todo x, com x ϵ R, é exatamente:
-10/3
-10
-2/3
-3
-1/3
Uma função é par se f(x) = f(-x) e ímpar se f(-x) = -f(x). A seguir são dados os esboços gráficos de função potência do tipo f(x) = xn para n = 1,2,3,4 e 5, respectivamente, em que x é a abscissa e f(x) a ordenada.

É correto afirmar que:
São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
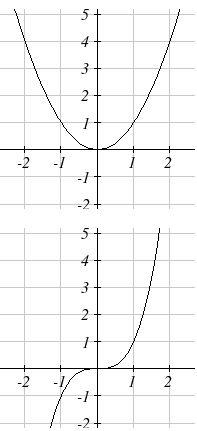
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
0,125 u.a
1 u.a
1,5 u.a
0,5 u.a
0,25 u.a
Considerando a equação 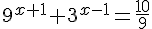 . O valor de
. O valor de 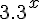 é exatamente:
é exatamente:
1/2
3
1
0
1/3
Resolva em 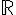 , a equação
, a equação  e marque a opção correta:
e marque a opção correta:
S = {3}
S = { }
S = {2}
S = {1}
S = {8}
Uma função composta pode ser determinada quando é possível comparar duas ou mais grandezas através de uma mesma função. Sejam f e g duas funções de R em R definidas por f(x) = 3x + k e g(x) = -2x + 5, sendo k uma constante real. O valor de k de modo que (fog)(x) = (gof)(x) para todo x, com x ϵ R, é exatamente:
-10/3
-10
-2/3
-3
-1/3
Uma função é par se f(x) = f(-x) e ímpar se f(-x) = -f(x). A seguir são dados os esboços gráficos de função potência do tipo f(x) = xn para n = 1,2,3,4 e 5, respectivamente, em que x é a abscissa e f(x) a ordenada.

É correto afirmar que:
São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
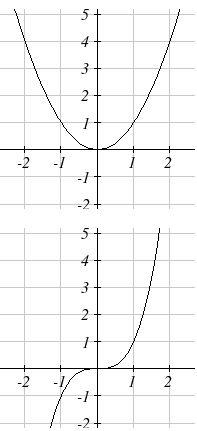
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
1/2
3
1
0
1/3
Resolva em  , a equação
, a equação  e marque a opção correta:
e marque a opção correta:
S = {3}
S = { }
S = {2}
S = {1}
S = {8}
Uma função composta pode ser determinada quando é possível comparar duas ou mais grandezas através de uma mesma função. Sejam f e g duas funções de R em R definidas por f(x) = 3x + k e g(x) = -2x + 5, sendo k uma constante real. O valor de k de modo que (fog)(x) = (gof)(x) para todo x, com x ϵ R, é exatamente:
-10/3
-10
-2/3
-3
-1/3
Uma função é par se f(x) = f(-x) e ímpar se f(-x) = -f(x). A seguir são dados os esboços gráficos de função potência do tipo f(x) = xn para n = 1,2,3,4 e 5, respectivamente, em que x é a abscissa e f(x) a ordenada.

É correto afirmar que:
São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
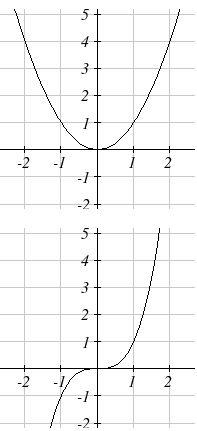
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
S = {3}
S = { }
S = {2}
S = {1}
S = {8}
Uma função composta pode ser determinada quando é possível comparar duas ou mais grandezas através de uma mesma função. Sejam f e g duas funções de R em R definidas por f(x) = 3x + k e g(x) = -2x + 5, sendo k uma constante real. O valor de k de modo que (fog)(x) = (gof)(x) para todo x, com x ϵ R, é exatamente:
-10/3
-10
-2/3
-3
-1/3
Uma função é par se f(x) = f(-x) e ímpar se f(-x) = -f(x). A seguir são dados os esboços gráficos de função potência do tipo f(x) = xn para n = 1,2,3,4 e 5, respectivamente, em que x é a abscissa e f(x) a ordenada.

É correto afirmar que:
São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
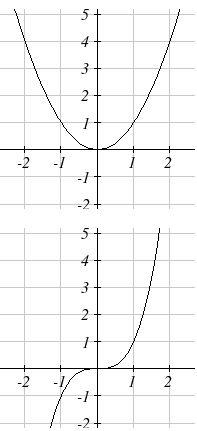
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
-10/3
-10
-2/3
-3
-1/3
Uma função é par se f(x) = f(-x) e ímpar se f(-x) = -f(x). A seguir são dados os esboços gráficos de função potência do tipo f(x) = xn para n = 1,2,3,4 e 5, respectivamente, em que x é a abscissa e f(x) a ordenada.

É correto afirmar que:
São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
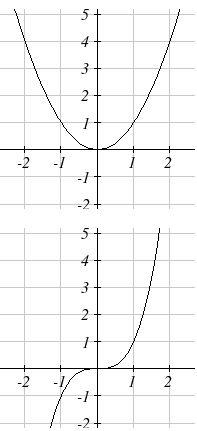
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:

São funções pares as funções III e V;
Somente a função I é uma função ímpar;
As funções I, II e V não são funções ímpares;
As funções II e IV são funções pares;
As funções I, II e V são ímpares;
Observem os gráficos,
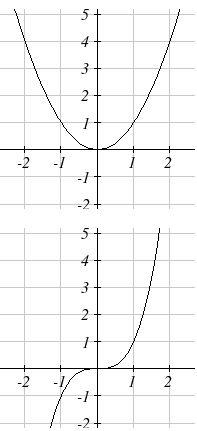
É correto afirmar:
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.
O custo unitário, em R$, de certo produto é calculado pelo setor administrativo de uma fábrica pela expressão %7D%3D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B%5Cleft%7C-%7B20%7D%7Bx%7D%2B%7B8%7D%5Cright%7C%7D) para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
para x < 20. Sendo x o número de peças fabricadas, o custo em R$ para fabricar 14 peças é exatamente:
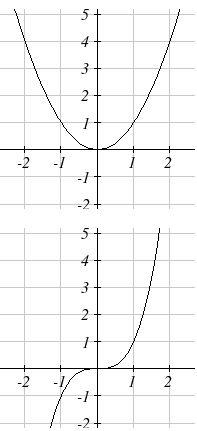
Ambos são função potência, com expoentes negativos.
A primeira não é função potência.
São funções potências, a primeira com expoente par e a segunda com expoente impar.
Ambos são função potência, com expoentes fracionários.
São funções potências, a primeira com esponte negativo e a segunda com expoente positivo.