GEOMETRIA ANALÍTICA
Assinale a alternativa que representa a distância focal da hipérbole de equação 25x2 – 9y2 = 225.
3
5
Considere os vetores %7D "vecu=(3,-1)")
e %7D. "vecv=(-1,2).")
Assinale a alternativa que contém o vetor %7D "vecx=(x,y)")
de forma que tenhamos a igualdade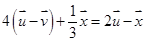 
.
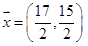
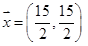
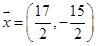
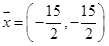
Os pontos A (-1,5) e B (2,1) são vértices consecutivos de um quadrado. Neste caso, o valor do comprimento da diagonal desse quadrado está corretamente representado na alternativa
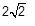
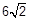
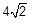
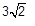
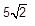
As coordenadas do centro e o raio das circunferências, cujas equações são c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa
c1: Centro = (5,0) e Raio =2
c2: Centro = (-2, 4 ) e Raio =1
c1: Centro = (5,4) e Raio =1
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (5,4) e Raio = 1
c2: Centro = (0,2 ) e Raio = 2
c1: Centro = (5,-4) e Raio = 2
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4,5) e Raio =1
c2: Centro = (2, 0 ) e Raio = 3
Sendo u = 5i + 4j + 3k; v = i + k, qual das alternativas abaixo representa u x v?
4i - 2j + 4k
4i - 8j + 4k
4i - 2j - 4k
4i + 8j - 4k
4i + 8j + 4k
O mapa abaixo mostra dois vetores que representam as distâncias entre Fernando de Noronha e as cidades Natal e Recife.
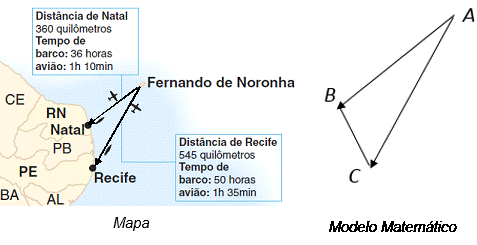
Sendo A (3, -3, 3), B (2, -1, 2) e C (1, 0, 2), podemos afirmar que:
I - O ângulo A formado pelos vetores AB e AC é igual a 10,9°
II - O ângulo B formado pelos vetores AB e BC é igual a 150°
III - O ângulo C formado pelos vetores BC e AC é igual a 19,1°
IV - A soma dos ângulos A e B é igual a 150°
V - A soma dos ângulos A e C é igual a 30°
Em relação as afirmativas acima são verdadeiras:
II e V, apenas.
I, III e V, apenas.
I, II, III e V, apenas.
I, II e III, apenas.
III e IV, apenas.
Em qual das alternativas abaixo temos o ponto P pertencente ao plano x0z, cuja cota é o triplo da abscissa, que dista 5 unidades de distância do ponto A (1, 3, -2).
%7D%3B%7BP%7D_%7B%7B%7B2%7D%7D%7D%7B%5Cleft(%5Cfrac%7B%7B%7B5%7D%2B%7B3%7D%5Csqrt%7B%7B15%7D%7D%7D%7D%7B%7B%7B10%7D%7D%7D%2C%7B0%7D%2C%5Cfrac%7B%7B%7B15%7D-%7B9%7D%5Csqrt%7B%7B15%7D%7D%7D%7D%7B%7B%7B10%7D%7D%7D%5Cright)%7D)
%7D%3B%7BP%7D_%7B%7B%7B2%7D%7D%7D%7B%5Cleft(%5Cfrac%7B%7B%7B1%7D%2B%5Csqrt%7B%7B%7B5%7D%7D%7D%7D%7D%7B%7B%7B5%7D%7D%7D%2C%7B0%7D%2C%5Cfrac%7B%7B%7B3%7D%2B%7B3%7D%5Csqrt%7B%7B%7B5%7D%7D%7D%7D%7D%7B%7B%7B5%7D%7D%7D%5Cright)%7D)
%7D%3B%7BP%7D_%7B%7B%7B2%7D%7D%7D%7B%5Cleft(%5Cfrac%7B%7B%7B15%7D%2B%7B3%7D%5Csqrt%7B%7B15%7D%7D%7D%7D%7B%7B%7B20%7D%7D%7D%2C%7B0%7D%2C%5Cfrac%7B%7B%7B15%7D-%7B9%7D%5Csqrt%7B%7B15%7D%7D%7D%7D%7B%7B%7B20%7D%7D%7D%5Cright)%7D)
%7D%3B%7BP%7D_%7B%7B%7B2%7D%7D%7D%7B%5Cleft(%5Cfrac%7B%7B-%7B5%7D%2B%7B3%7D%5Csqrt%7B%7B%7B15%7D%7D%7D%7D%7D%7B%7B%7B10%7D%7D%7D%2C%7B0%7D%2C%5Cfrac%7B%7B-%7B15%7D%2B%7B9%7D%5Csqrt%7B%7B%7B15%7D%7D%7D%7D%7D%7B%7B%7B10%7D%7D%7D%5Cright)%7D)
%7D%3B%7BP%7D_%7B%7B%7B2%7D%7D%7D%7B%5Cleft(%5Cfrac%7B%7B%7B1%7D%2B%5Csqrt%7B%7B%7B5%7D%7D%7D%7D%7D%7B%7B%7B2%7D%7D%7D%2C%7B0%7D%2C%7B6%7D%5Csqrt%7B%7B%7B5%7D%7D%7D%5Cright)%7D)
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
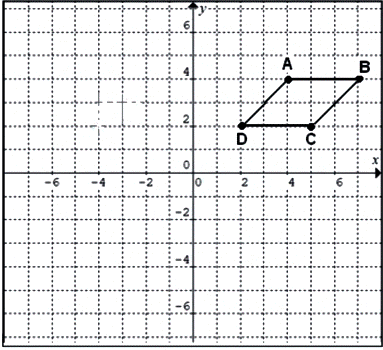
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
3
5
Considere os vetores e Assinale a alternativa que contém o vetor de forma que tenhamos a igualdade .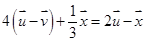
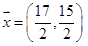
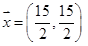
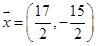
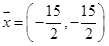
Os pontos A (-1,5) e B (2,1) são vértices consecutivos de um quadrado. Neste caso, o valor do comprimento da diagonal desse quadrado está corretamente representado na alternativa
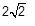
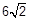
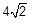
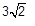
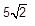
As coordenadas do centro e o raio das circunferências, cujas equações são c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa
c1: Centro = (5,0) e Raio =2
c2: Centro = (-2, 4 ) e Raio =1
c1: Centro = (5,4) e Raio =1
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (5,4) e Raio = 1
c2: Centro = (0,2 ) e Raio = 2
c1: Centro = (5,-4) e Raio = 2
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4,5) e Raio =1
c2: Centro = (2, 0 ) e Raio = 3
Sendo u = 5i + 4j + 3k; v = i + k, qual das alternativas abaixo representa u x v?
4i - 2j + 4k
4i - 8j + 4k
4i - 2j - 4k
4i + 8j - 4k
4i + 8j + 4k
O mapa abaixo mostra dois vetores que representam as distâncias entre Fernando de Noronha e as cidades Natal e Recife.
Sendo A (3, -3, 3), B (2, -1, 2) e C (1, 0, 2), podemos afirmar que:
I - O ângulo A formado pelos vetores AB e AC é igual a 10,9°
II - O ângulo B formado pelos vetores AB e BC é igual a 150°
III - O ângulo C formado pelos vetores BC e AC é igual a 19,1°
IV - A soma dos ângulos A e B é igual a 150°
V - A soma dos ângulos A e C é igual a 30°
Em relação as afirmativas acima são verdadeiras:
II e V, apenas.
I, III e V, apenas.
I, II, III e V, apenas.
I, II e III, apenas.
III e IV, apenas.
Em qual das alternativas abaixo temos o ponto P pertencente ao plano x0z, cuja cota é o triplo da abscissa, que dista 5 unidades de distância do ponto A (1, 3, -2).
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
.
Os pontos A (-1,5) e B (2,1) são vértices consecutivos de um quadrado. Neste caso, o valor do comprimento da diagonal desse quadrado está corretamente representado na alternativa
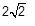
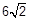
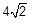
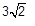
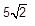
As coordenadas do centro e o raio das circunferências, cujas equações são c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa
c1: Centro = (5,0) e Raio =2
c2: Centro = (-2, 4 ) e Raio =1
c1: Centro = (5,4) e Raio =1
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (5,4) e Raio = 1
c2: Centro = (0,2 ) e Raio = 2
c1: Centro = (5,-4) e Raio = 2
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4,5) e Raio =1
c2: Centro = (2, 0 ) e Raio = 3
Sendo u = 5i + 4j + 3k; v = i + k, qual das alternativas abaixo representa u x v?
4i - 2j + 4k
4i - 8j + 4k
4i - 2j - 4k
4i + 8j - 4k
4i + 8j + 4k
O mapa abaixo mostra dois vetores que representam as distâncias entre Fernando de Noronha e as cidades Natal e Recife.
Sendo A (3, -3, 3), B (2, -1, 2) e C (1, 0, 2), podemos afirmar que:
I - O ângulo A formado pelos vetores AB e AC é igual a 10,9°
II - O ângulo B formado pelos vetores AB e BC é igual a 150°
III - O ângulo C formado pelos vetores BC e AC é igual a 19,1°
IV - A soma dos ângulos A e B é igual a 150°
V - A soma dos ângulos A e C é igual a 30°
Em relação as afirmativas acima são verdadeiras:
II e V, apenas.
I, III e V, apenas.
I, II, III e V, apenas.
I, II e III, apenas.
III e IV, apenas.
Em qual das alternativas abaixo temos o ponto P pertencente ao plano x0z, cuja cota é o triplo da abscissa, que dista 5 unidades de distância do ponto A (1, 3, -2).
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
As coordenadas do centro e o raio das circunferências, cujas equações são c1: (x – 5)2 + (y – 4)2 = 1 e c2: (x – 2)2 + y2 = 4, estão representadas na alternativa
c1: Centro = (5,0) e Raio =2
c2: Centro = (-2, 4 ) e Raio =1
c1: Centro = (5,4) e Raio =1
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (5,4) e Raio = 1
c2: Centro = (0,2 ) e Raio = 2
c1: Centro = (5,-4) e Raio = 2
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4,5) e Raio =1
c2: Centro = (2, 0 ) e Raio = 3
Sendo u = 5i + 4j + 3k; v = i + k, qual das alternativas abaixo representa u x v?
4i - 2j + 4k
4i - 8j + 4k
4i - 2j - 4k
4i + 8j - 4k
4i + 8j + 4k
O mapa abaixo mostra dois vetores que representam as distâncias entre Fernando de Noronha e as cidades Natal e Recife.
Sendo A (3, -3, 3), B (2, -1, 2) e C (1, 0, 2), podemos afirmar que:
I - O ângulo A formado pelos vetores AB e AC é igual a 10,9°
II - O ângulo B formado pelos vetores AB e BC é igual a 150°
III - O ângulo C formado pelos vetores BC e AC é igual a 19,1°
IV - A soma dos ângulos A e B é igual a 150°
V - A soma dos ângulos A e C é igual a 30°
Em relação as afirmativas acima são verdadeiras:
II e V, apenas.
I, III e V, apenas.
I, II, III e V, apenas.
I, II e III, apenas.
III e IV, apenas.
Em qual das alternativas abaixo temos o ponto P pertencente ao plano x0z, cuja cota é o triplo da abscissa, que dista 5 unidades de distância do ponto A (1, 3, -2).
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
c1: Centro = (5,0) e Raio =2
c2: Centro = (-2, 4 ) e Raio =1
c1: Centro = (5,4) e Raio =1
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (5,4) e Raio = 1
c2: Centro = (0,2 ) e Raio = 2
c1: Centro = (5,-4) e Raio = 2
c2: Centro = (2, 0 ) e Raio = 2
c1: Centro = (4,5) e Raio =1
c2: Centro = (2, 0 ) e Raio = 3
Sendo u = 5i + 4j + 3k; v = i + k, qual das alternativas abaixo representa u x v?
4i - 2j + 4k
4i - 8j + 4k
4i - 2j - 4k
4i + 8j - 4k
4i + 8j + 4k
O mapa abaixo mostra dois vetores que representam as distâncias entre Fernando de Noronha e as cidades Natal e Recife.
Sendo A (3, -3, 3), B (2, -1, 2) e C (1, 0, 2), podemos afirmar que:
I - O ângulo A formado pelos vetores AB e AC é igual a 10,9°
II - O ângulo B formado pelos vetores AB e BC é igual a 150°
III - O ângulo C formado pelos vetores BC e AC é igual a 19,1°
IV - A soma dos ângulos A e B é igual a 150°
V - A soma dos ângulos A e C é igual a 30°
Em relação as afirmativas acima são verdadeiras:
II e V, apenas.
I, III e V, apenas.
I, II, III e V, apenas.
I, II e III, apenas.
III e IV, apenas.
Em qual das alternativas abaixo temos o ponto P pertencente ao plano x0z, cuja cota é o triplo da abscissa, que dista 5 unidades de distância do ponto A (1, 3, -2).
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
4i - 2j + 4k
4i - 8j + 4k
4i - 2j - 4k
4i + 8j - 4k
4i + 8j + 4k
O mapa abaixo mostra dois vetores que representam as distâncias entre Fernando de Noronha e as cidades Natal e Recife.
Sendo A (3, -3, 3), B (2, -1, 2) e C (1, 0, 2), podemos afirmar que:
I - O ângulo A formado pelos vetores AB e AC é igual a 10,9°
II - O ângulo B formado pelos vetores AB e BC é igual a 150°
III - O ângulo C formado pelos vetores BC e AC é igual a 19,1°
IV - A soma dos ângulos A e B é igual a 150°
V - A soma dos ângulos A e C é igual a 30°
Em relação as afirmativas acima são verdadeiras:
II e V, apenas.
I, III e V, apenas.
I, II, III e V, apenas.
I, II e III, apenas.
III e IV, apenas.
Em qual das alternativas abaixo temos o ponto P pertencente ao plano x0z, cuja cota é o triplo da abscissa, que dista 5 unidades de distância do ponto A (1, 3, -2).
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
II e V, apenas.
I, III e V, apenas.
I, II, III e V, apenas.
I, II e III, apenas.
III e IV, apenas.
Em qual das alternativas abaixo temos o ponto P pertencente ao plano x0z, cuja cota é o triplo da abscissa, que dista 5 unidades de distância do ponto A (1, 3, -2).
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
O sistema cartesiano apresentado a seguir é a representação matemática do mapa de uma cidade. Nele está traçado um paralelogramo ABCD, onde A, B, C e D representam pontos turísticos da cidade. O paralelogramo ABCD é o local onde estão localizados os hotéis dessa cidade.
Em quais dos pontos do plano os hotéis dessa cidade estão localizados?
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
(4,4); (4,7); (2,5); (2,2)
(2, 2); (5, 2); (4, 4); (7, 4)
(2,2); (5,2); (4,4); (7,4)
(4,4); (7,4); (5,2); (2,2)
(2,2); (5,2); (4,4); (7,4)
Calcule o ângulo entre as retas:
e assinale a alternativa correspondente.
