ESTATÍSTICA INFERENCIAL
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 500.)
Os escritórios de admissão do Clearwater College estimaram a seguinte equação de regressão, relacionando a média final acadêmica dos estudantes com a pontuação obtida em matemática e a pontuação obtida no ensino médio.
, em que:
x1 = média no ensino médio;
x2 = pontuação em matemática;
y = média final acadêmica.
A respeito da interpretação da equação estimada, assinale a alternativa correta.
A média final acadêmica é a variável independente e a pontuação em matemática é a variável dependente.
Quanto maior a pontuação em matemática, menor a média acadêmica.
Quanto menor a média no ensino médio, maior a média acadêmica.
Para cada 1,0 ponto a mais na média do ensino médio, espera-se um acréscimo de 0,0235 na média final acadêmica.
Se a média no ensino médio e a pontuação em matemática forem nulas, espera-se a média final acadêmica igual a + 1,41
b
a
d
c
e
d
b
e
a
c
a
d
c
e
b
d
a
c
b
e
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
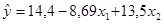, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
25,60 pontos.
28,49 pontos.
58,46 pontos.
98,57 pontos.
67,39 pontos
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 493.)
A Heller Company fabrica cortadores de grama e equipamentos relacionados aos cortadores. Os gerentes acreditam que a quantidade de cortadores vendidos depende dos preços da companhia e do concorrente. Seja:
y = quantidade vendida (1.000)
x1= preço do cortador do concorrente (US$)
x2 = preço do cortador da Heller (US$)
Os gerentes queriam uma equação de regressão estimada que relacionasse a quantidade vendida com os preços do cortador da Heller e do concorrente. Após obter os preços em 10 cidades, foi feita a análise dos dados na planilha eletrônica Excel, sendo obtidos os seguintes resultados:
Estatística F crítica para 5% de significância e (2; 7) graus de liberdade: 4,74.
Estatística t crítica para 5% de significância e 7 graus de liberdade: 1,895.
Com base nos resultados apresentados no relatório de saída do Excel, julgue as seguintes afirmações:
1. A equação de regressão estimada que pode ser usada para prever a quantidade vendida dados o preço do concorrente e o preço da Heller é descrita por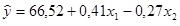 
.
2. O preço do cortador do concorrente e o preço da Heller explicam conjuntamente 65,3% das variações nas quantidades vendidas da Heller.
3. O resultado do teste de análise da variância rejeita a hipótese nula de que o preço do cortador do concorrente e o preço da Heller não explicam as quantidades vendidas da Heller.
4. O resultado do teste t para o coeficiente da variável x1 permite concluir que isoladamente o preço do concorrente não é uma variável significante para explicar as variações nas quantidades vendidas da Heller.
5. A equação estimada mostra que quanto maior o preço do cortador de grama da Heller menor será a quantidade vendida, pois o sinal da variável x2 é negativo.
Estão corretas as afirmações:
2, 3 e 4, somente.
3, 4 e 5, somente.
1, 2, 3, 4 e 5.
1, 2, 3 e 4, somente.
1, 2 e 3, somente.
ENADE 2006. Adaptada.
A legislação de trânsito brasileira considera que o condutor de um veículo está dirigindo alcoolizado quando o teor alcoólico de seu sangue excede 0,6 gramas de álcool por litro de sangue. O gráfico abaixo mostra o processo de absorção e eliminação do álcool quando um indivíduo bebe, em um curto espaço de tempo, de 1 a 4 latas de cerveja.
(Fonte: National Health Institute, Estados Unidos)
Considere as afirmativas a seguir.
I - O álcool é eliminado pelo organismo muito mais lentamente do que é absorvido.
II - Uma pessoa que vá dirigir imediatamente após ingerir uma lata de cerveja não será multada.
III - Se o indivíduo A toma rapidamente três latas de cerveja e o indivíduo B toma quatro latas, o organismo do indivíduo A elimina o álcool contido na bebida mais rapidamente do que o organismo do indivíduo B.
Está(ão) correta(s) a(s) afirmativa(s)
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
, em que:A média final acadêmica é a variável independente e a pontuação em matemática é a variável dependente.
Quanto maior a pontuação em matemática, menor a média acadêmica.
Quanto menor a média no ensino médio, maior a média acadêmica.
Para cada 1,0 ponto a mais na média do ensino médio, espera-se um acréscimo de 0,0235 na média final acadêmica.
Se a média no ensino médio e a pontuação em matemática forem nulas, espera-se a média final acadêmica igual a + 1,41
b
a
d
c
e
d
b
e
a
c
a
d
c
e
b
d
a
c
b
e
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
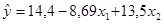, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
25,60 pontos.
28,49 pontos.
58,46 pontos.
98,57 pontos.
67,39 pontos
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 493.)
A Heller Company fabrica cortadores de grama e equipamentos relacionados aos cortadores. Os gerentes acreditam que a quantidade de cortadores vendidos depende dos preços da companhia e do concorrente. Seja:
y = quantidade vendida (1.000)
x1= preço do cortador do concorrente (US$)
x2 = preço do cortador da Heller (US$)
Os gerentes queriam uma equação de regressão estimada que relacionasse a quantidade vendida com os preços do cortador da Heller e do concorrente. Após obter os preços em 10 cidades, foi feita a análise dos dados na planilha eletrônica Excel, sendo obtidos os seguintes resultados:
Estatística F crítica para 5% de significância e (2; 7) graus de liberdade: 4,74.
Estatística t crítica para 5% de significância e 7 graus de liberdade: 1,895.
Com base nos resultados apresentados no relatório de saída do Excel, julgue as seguintes afirmações:
1. A equação de regressão estimada que pode ser usada para prever a quantidade vendida dados o preço do concorrente e o preço da Heller é descrita por .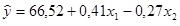
2. O preço do cortador do concorrente e o preço da Heller explicam conjuntamente 65,3% das variações nas quantidades vendidas da Heller.
3. O resultado do teste de análise da variância rejeita a hipótese nula de que o preço do cortador do concorrente e o preço da Heller não explicam as quantidades vendidas da Heller.
4. O resultado do teste t para o coeficiente da variável x1 permite concluir que isoladamente o preço do concorrente não é uma variável significante para explicar as variações nas quantidades vendidas da Heller.
5. A equação estimada mostra que quanto maior o preço do cortador de grama da Heller menor será a quantidade vendida, pois o sinal da variável x2 é negativo.
Estão corretas as afirmações:
2, 3 e 4, somente.
3, 4 e 5, somente.
1, 2, 3, 4 e 5.
1, 2, 3 e 4, somente.
1, 2 e 3, somente.
ENADE 2006. Adaptada.
A legislação de trânsito brasileira considera que o condutor de um veículo está dirigindo alcoolizado quando o teor alcoólico de seu sangue excede 0,6 gramas de álcool por litro de sangue. O gráfico abaixo mostra o processo de absorção e eliminação do álcool quando um indivíduo bebe, em um curto espaço de tempo, de 1 a 4 latas de cerveja.
(Fonte: National Health Institute, Estados Unidos)
Considere as afirmativas a seguir.
I - O álcool é eliminado pelo organismo muito mais lentamente do que é absorvido.
II - Uma pessoa que vá dirigir imediatamente após ingerir uma lata de cerveja não será multada.
III - Se o indivíduo A toma rapidamente três latas de cerveja e o indivíduo B toma quatro latas, o organismo do indivíduo A elimina o álcool contido na bebida mais rapidamente do que o organismo do indivíduo B.
Está(ão) correta(s) a(s) afirmativa(s)
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
b
a
d
c
e
d
b
e
a
c
a
d
c
e
b
d
a
c
b
e
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
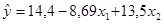, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
25,60 pontos.
28,49 pontos.
58,46 pontos.
98,57 pontos.
67,39 pontos
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 493.)
A Heller Company fabrica cortadores de grama e equipamentos relacionados aos cortadores. Os gerentes acreditam que a quantidade de cortadores vendidos depende dos preços da companhia e do concorrente. Seja:
y = quantidade vendida (1.000)
x1= preço do cortador do concorrente (US$)
x2 = preço do cortador da Heller (US$)
Os gerentes queriam uma equação de regressão estimada que relacionasse a quantidade vendida com os preços do cortador da Heller e do concorrente. Após obter os preços em 10 cidades, foi feita a análise dos dados na planilha eletrônica Excel, sendo obtidos os seguintes resultados:
Estatística F crítica para 5% de significância e (2; 7) graus de liberdade: 4,74.
Estatística t crítica para 5% de significância e 7 graus de liberdade: 1,895.
Com base nos resultados apresentados no relatório de saída do Excel, julgue as seguintes afirmações:
1. A equação de regressão estimada que pode ser usada para prever a quantidade vendida dados o preço do concorrente e o preço da Heller é descrita por .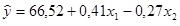
2. O preço do cortador do concorrente e o preço da Heller explicam conjuntamente 65,3% das variações nas quantidades vendidas da Heller.
3. O resultado do teste de análise da variância rejeita a hipótese nula de que o preço do cortador do concorrente e o preço da Heller não explicam as quantidades vendidas da Heller.
4. O resultado do teste t para o coeficiente da variável x1 permite concluir que isoladamente o preço do concorrente não é uma variável significante para explicar as variações nas quantidades vendidas da Heller.
5. A equação estimada mostra que quanto maior o preço do cortador de grama da Heller menor será a quantidade vendida, pois o sinal da variável x2 é negativo.
Estão corretas as afirmações:
2, 3 e 4, somente.
3, 4 e 5, somente.
1, 2, 3, 4 e 5.
1, 2, 3 e 4, somente.
1, 2 e 3, somente.
ENADE 2006. Adaptada.
A legislação de trânsito brasileira considera que o condutor de um veículo está dirigindo alcoolizado quando o teor alcoólico de seu sangue excede 0,6 gramas de álcool por litro de sangue. O gráfico abaixo mostra o processo de absorção e eliminação do álcool quando um indivíduo bebe, em um curto espaço de tempo, de 1 a 4 latas de cerveja.
(Fonte: National Health Institute, Estados Unidos)
Considere as afirmativas a seguir.
I - O álcool é eliminado pelo organismo muito mais lentamente do que é absorvido.
II - Uma pessoa que vá dirigir imediatamente após ingerir uma lata de cerveja não será multada.
III - Se o indivíduo A toma rapidamente três latas de cerveja e o indivíduo B toma quatro latas, o organismo do indivíduo A elimina o álcool contido na bebida mais rapidamente do que o organismo do indivíduo B.
Está(ão) correta(s) a(s) afirmativa(s)
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
d
b
e
a
c
a
d
c
e
b
d
a
c
b
e
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
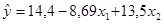, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
25,60 pontos.
28,49 pontos.
58,46 pontos.
98,57 pontos.
67,39 pontos
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 493.)
A Heller Company fabrica cortadores de grama e equipamentos relacionados aos cortadores. Os gerentes acreditam que a quantidade de cortadores vendidos depende dos preços da companhia e do concorrente. Seja:
y = quantidade vendida (1.000)
x1= preço do cortador do concorrente (US$)
x2 = preço do cortador da Heller (US$)
Os gerentes queriam uma equação de regressão estimada que relacionasse a quantidade vendida com os preços do cortador da Heller e do concorrente. Após obter os preços em 10 cidades, foi feita a análise dos dados na planilha eletrônica Excel, sendo obtidos os seguintes resultados:
Estatística F crítica para 5% de significância e (2; 7) graus de liberdade: 4,74.
Estatística t crítica para 5% de significância e 7 graus de liberdade: 1,895.
Com base nos resultados apresentados no relatório de saída do Excel, julgue as seguintes afirmações:
1. A equação de regressão estimada que pode ser usada para prever a quantidade vendida dados o preço do concorrente e o preço da Heller é descrita por .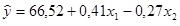
2. O preço do cortador do concorrente e o preço da Heller explicam conjuntamente 65,3% das variações nas quantidades vendidas da Heller.
3. O resultado do teste de análise da variância rejeita a hipótese nula de que o preço do cortador do concorrente e o preço da Heller não explicam as quantidades vendidas da Heller.
4. O resultado do teste t para o coeficiente da variável x1 permite concluir que isoladamente o preço do concorrente não é uma variável significante para explicar as variações nas quantidades vendidas da Heller.
5. A equação estimada mostra que quanto maior o preço do cortador de grama da Heller menor será a quantidade vendida, pois o sinal da variável x2 é negativo.
Estão corretas as afirmações:
2, 3 e 4, somente.
3, 4 e 5, somente.
1, 2, 3, 4 e 5.
1, 2, 3 e 4, somente.
1, 2 e 3, somente.
ENADE 2006. Adaptada.
A legislação de trânsito brasileira considera que o condutor de um veículo está dirigindo alcoolizado quando o teor alcoólico de seu sangue excede 0,6 gramas de álcool por litro de sangue. O gráfico abaixo mostra o processo de absorção e eliminação do álcool quando um indivíduo bebe, em um curto espaço de tempo, de 1 a 4 latas de cerveja.
(Fonte: National Health Institute, Estados Unidos)
Considere as afirmativas a seguir.
I - O álcool é eliminado pelo organismo muito mais lentamente do que é absorvido.
II - Uma pessoa que vá dirigir imediatamente após ingerir uma lata de cerveja não será multada.
III - Se o indivíduo A toma rapidamente três latas de cerveja e o indivíduo B toma quatro latas, o organismo do indivíduo A elimina o álcool contido na bebida mais rapidamente do que o organismo do indivíduo B.
Está(ão) correta(s) a(s) afirmativa(s)
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
a
d
c
e
b
d
a
c
b
e
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
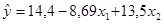, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
25,60 pontos.
28,49 pontos.
58,46 pontos.
98,57 pontos.
67,39 pontos
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 493.)
A Heller Company fabrica cortadores de grama e equipamentos relacionados aos cortadores. Os gerentes acreditam que a quantidade de cortadores vendidos depende dos preços da companhia e do concorrente. Seja:
y = quantidade vendida (1.000)
x1= preço do cortador do concorrente (US$)
x2 = preço do cortador da Heller (US$)
Os gerentes queriam uma equação de regressão estimada que relacionasse a quantidade vendida com os preços do cortador da Heller e do concorrente. Após obter os preços em 10 cidades, foi feita a análise dos dados na planilha eletrônica Excel, sendo obtidos os seguintes resultados:
Estatística F crítica para 5% de significância e (2; 7) graus de liberdade: 4,74.
Estatística t crítica para 5% de significância e 7 graus de liberdade: 1,895.
Com base nos resultados apresentados no relatório de saída do Excel, julgue as seguintes afirmações:
1. A equação de regressão estimada que pode ser usada para prever a quantidade vendida dados o preço do concorrente e o preço da Heller é descrita por .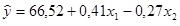
2. O preço do cortador do concorrente e o preço da Heller explicam conjuntamente 65,3% das variações nas quantidades vendidas da Heller.
3. O resultado do teste de análise da variância rejeita a hipótese nula de que o preço do cortador do concorrente e o preço da Heller não explicam as quantidades vendidas da Heller.
4. O resultado do teste t para o coeficiente da variável x1 permite concluir que isoladamente o preço do concorrente não é uma variável significante para explicar as variações nas quantidades vendidas da Heller.
5. A equação estimada mostra que quanto maior o preço do cortador de grama da Heller menor será a quantidade vendida, pois o sinal da variável x2 é negativo.
Estão corretas as afirmações:
2, 3 e 4, somente.
3, 4 e 5, somente.
1, 2, 3, 4 e 5.
1, 2, 3 e 4, somente.
1, 2 e 3, somente.
ENADE 2006. Adaptada.
A legislação de trânsito brasileira considera que o condutor de um veículo está dirigindo alcoolizado quando o teor alcoólico de seu sangue excede 0,6 gramas de álcool por litro de sangue. O gráfico abaixo mostra o processo de absorção e eliminação do álcool quando um indivíduo bebe, em um curto espaço de tempo, de 1 a 4 latas de cerveja.
(Fonte: National Health Institute, Estados Unidos)
Considere as afirmativas a seguir.
I - O álcool é eliminado pelo organismo muito mais lentamente do que é absorvido.
II - Uma pessoa que vá dirigir imediatamente após ingerir uma lata de cerveja não será multada.
III - Se o indivíduo A toma rapidamente três latas de cerveja e o indivíduo B toma quatro latas, o organismo do indivíduo A elimina o álcool contido na bebida mais rapidamente do que o organismo do indivíduo B.
Está(ão) correta(s) a(s) afirmativa(s)
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
d
a
c
b
e
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
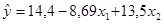, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
25,60 pontos.
28,49 pontos.
58,46 pontos.
98,57 pontos.
67,39 pontos
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 493.)
A Heller Company fabrica cortadores de grama e equipamentos relacionados aos cortadores. Os gerentes acreditam que a quantidade de cortadores vendidos depende dos preços da companhia e do concorrente. Seja:
y = quantidade vendida (1.000)
x1= preço do cortador do concorrente (US$)
x2 = preço do cortador da Heller (US$)
Os gerentes queriam uma equação de regressão estimada que relacionasse a quantidade vendida com os preços do cortador da Heller e do concorrente. Após obter os preços em 10 cidades, foi feita a análise dos dados na planilha eletrônica Excel, sendo obtidos os seguintes resultados:
Estatística F crítica para 5% de significância e (2; 7) graus de liberdade: 4,74.
Estatística t crítica para 5% de significância e 7 graus de liberdade: 1,895.
Com base nos resultados apresentados no relatório de saída do Excel, julgue as seguintes afirmações:
1. A equação de regressão estimada que pode ser usada para prever a quantidade vendida dados o preço do concorrente e o preço da Heller é descrita por .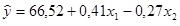
2. O preço do cortador do concorrente e o preço da Heller explicam conjuntamente 65,3% das variações nas quantidades vendidas da Heller.
3. O resultado do teste de análise da variância rejeita a hipótese nula de que o preço do cortador do concorrente e o preço da Heller não explicam as quantidades vendidas da Heller.
4. O resultado do teste t para o coeficiente da variável x1 permite concluir que isoladamente o preço do concorrente não é uma variável significante para explicar as variações nas quantidades vendidas da Heller.
5. A equação estimada mostra que quanto maior o preço do cortador de grama da Heller menor será a quantidade vendida, pois o sinal da variável x2 é negativo.
Estão corretas as afirmações:
2, 3 e 4, somente.
3, 4 e 5, somente.
1, 2, 3, 4 e 5.
1, 2, 3 e 4, somente.
1, 2 e 3, somente.
ENADE 2006. Adaptada.
A legislação de trânsito brasileira considera que o condutor de um veículo está dirigindo alcoolizado quando o teor alcoólico de seu sangue excede 0,6 gramas de álcool por litro de sangue. O gráfico abaixo mostra o processo de absorção e eliminação do álcool quando um indivíduo bebe, em um curto espaço de tempo, de 1 a 4 latas de cerveja.
(Fonte: National Health Institute, Estados Unidos)
Considere as afirmativas a seguir.
I - O álcool é eliminado pelo organismo muito mais lentamente do que é absorvido.
II - Uma pessoa que vá dirigir imediatamente após ingerir uma lata de cerveja não será multada.
III - Se o indivíduo A toma rapidamente três latas de cerveja e o indivíduo B toma quatro latas, o organismo do indivíduo A elimina o álcool contido na bebida mais rapidamente do que o organismo do indivíduo B.
Está(ão) correta(s) a(s) afirmativa(s)
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
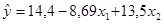, em que:25,60 pontos.
28,49 pontos.
58,46 pontos.
98,57 pontos.
67,39 pontos
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 493.)
A Heller Company fabrica cortadores de grama e equipamentos relacionados aos cortadores. Os gerentes acreditam que a quantidade de cortadores vendidos depende dos preços da companhia e do concorrente. Seja:
y = quantidade vendida (1.000)
x1= preço do cortador do concorrente (US$)
x2 = preço do cortador da Heller (US$)
Os gerentes queriam uma equação de regressão estimada que relacionasse a quantidade vendida com os preços do cortador da Heller e do concorrente. Após obter os preços em 10 cidades, foi feita a análise dos dados na planilha eletrônica Excel, sendo obtidos os seguintes resultados:
Estatística F crítica para 5% de significância e (2; 7) graus de liberdade: 4,74.
Estatística t crítica para 5% de significância e 7 graus de liberdade: 1,895.
Com base nos resultados apresentados no relatório de saída do Excel, julgue as seguintes afirmações:
1. A equação de regressão estimada que pode ser usada para prever a quantidade vendida dados o preço do concorrente e o preço da Heller é descrita por .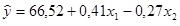
2. O preço do cortador do concorrente e o preço da Heller explicam conjuntamente 65,3% das variações nas quantidades vendidas da Heller.
3. O resultado do teste de análise da variância rejeita a hipótese nula de que o preço do cortador do concorrente e o preço da Heller não explicam as quantidades vendidas da Heller.
4. O resultado do teste t para o coeficiente da variável x1 permite concluir que isoladamente o preço do concorrente não é uma variável significante para explicar as variações nas quantidades vendidas da Heller.
5. A equação estimada mostra que quanto maior o preço do cortador de grama da Heller menor será a quantidade vendida, pois o sinal da variável x2 é negativo.
Estão corretas as afirmações:
2, 3 e 4, somente.
3, 4 e 5, somente.
1, 2, 3, 4 e 5.
1, 2, 3 e 4, somente.
1, 2 e 3, somente.
ENADE 2006. Adaptada.
A legislação de trânsito brasileira considera que o condutor de um veículo está dirigindo alcoolizado quando o teor alcoólico de seu sangue excede 0,6 gramas de álcool por litro de sangue. O gráfico abaixo mostra o processo de absorção e eliminação do álcool quando um indivíduo bebe, em um curto espaço de tempo, de 1 a 4 latas de cerveja.
(Fonte: National Health Institute, Estados Unidos)
Considere as afirmativas a seguir.
I - O álcool é eliminado pelo organismo muito mais lentamente do que é absorvido.
II - Uma pessoa que vá dirigir imediatamente após ingerir uma lata de cerveja não será multada.
III - Se o indivíduo A toma rapidamente três latas de cerveja e o indivíduo B toma quatro latas, o organismo do indivíduo A elimina o álcool contido na bebida mais rapidamente do que o organismo do indivíduo B.
Está(ão) correta(s) a(s) afirmativa(s)
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
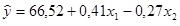.2, 3 e 4, somente.
3, 4 e 5, somente.
1, 2, 3, 4 e 5.
1, 2, 3 e 4, somente.
1, 2 e 3, somente.
ENADE 2006. Adaptada.
A legislação de trânsito brasileira considera que o condutor de um veículo está dirigindo alcoolizado quando o teor alcoólico de seu sangue excede 0,6 gramas de álcool por litro de sangue. O gráfico abaixo mostra o processo de absorção e eliminação do álcool quando um indivíduo bebe, em um curto espaço de tempo, de 1 a 4 latas de cerveja.
(Fonte: National Health Institute, Estados Unidos)
Considere as afirmativas a seguir.
I - O álcool é eliminado pelo organismo muito mais lentamente do que é absorvido.
II - Uma pessoa que vá dirigir imediatamente após ingerir uma lata de cerveja não será multada.
III - Se o indivíduo A toma rapidamente três latas de cerveja e o indivíduo B toma quatro latas, o organismo do indivíduo A elimina o álcool contido na bebida mais rapidamente do que o organismo do indivíduo B.
Está(ão) correta(s) a(s) afirmativa(s)
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
I, II e III.
I e III, apenas.
II e III, apenas.
II, apenas.
I e II, apenas.
Para verificar se determinada linha de produção estava bem ajustada, o controlador de qualidade selecionou aleatoriamente uma amostra simples de 49 peças, encontrando a média amostral igual a 25 g. O controlador sabe, de estudos anteriores, que o desvio padrão dos pesos da população de peças é igual a 5 g. Nessas condições, qual a margem de erro para uma probabilidade de 99%? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
