ELETRÔNICA ANALÓGICA I
Dadas as informações fornecidas na figura abaixo, determine:
(I) β, (II) Vcc e (III) RB
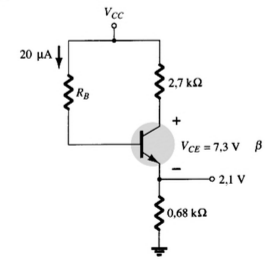
(I) 200; (II) 13,12V (III) 747 kOhm
(I) 105; (II) 17,74V (III) 747 kOhm
(I) 244; (II) 12,55V (III) 910 kOhm
(I) 154,4; (II) 15,11V (III) 565 kOhm
(I) 154,4; (II) 17,74V (III) 747 kOhm
Determine o valor de para cada circuito da figura abaixo.
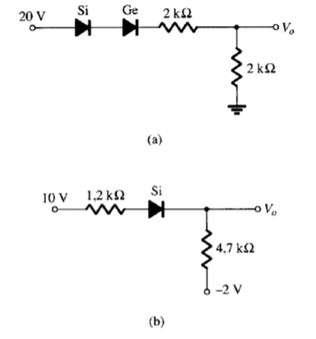
(a) Vo = 0 V (b) Vo = 7,96 V
(a) Vo = 9,3 V (b) Vo = 7 V
(a) Vo = 9,5 V (b) Vo = 7,96 V
(a) Vo = 9,5 V (b) Vo = 7 V
(a) Vo = 0 V (b) Vo = 7 V
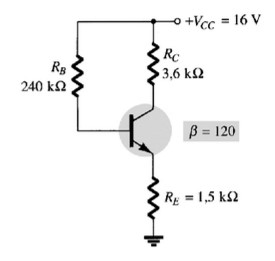
Para o circuito da figura abaixo:
(a) Vc aumenta ou diminui quando RB aumenta?
(b) IC aumenta ou diminui quando B é reduzido?
(c) O que acontece com a corrente de saturação quando B aumenta?
(d) A corrente do coletor aumenta ou diminui quando VCC é reduzida?
(e) O que acontece com VCE se o transistor é substituído por outro com B menor?
(a) RB aumenta, IB aumenta, IC diminui, VC aumenta; (b) Beta diminui, IC diminui; (c) diminui; (d) VCC aumenta, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC aumenta, VRE diminui, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC diminui; (b) Beta diminui, IC aumenta; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC diminui, VRE aumenta, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC aumenta; (b) Beta diminui, IC aumenta; (c) aumenta; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC aumenta, VRC diminui, VRE aumenta, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC aumenta; (b) Beta diminui, IC diminui; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC diminui, VRE diminui, VCE aumenta
(a) RB aumenta, IB diminui, IC aumenta, VC aumenta; (b) Beta diminui, IC aumenta; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC aumenta, VRC diminui, VRE diminui, VCE aumenta
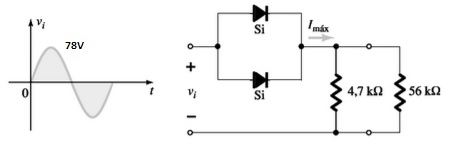
Dado o circuito abaixo responda:
(a) Dado Pmáx = 14 mW para cada diodo da figura, determine a corrente máxima nominal de cada diodo (utilizando o modelo equivalente aproximado).
(b) Determine Imáx para Vimáx = 78 V.
(c) Determine a corrente através de cada diodo para Vimáx utilizando os resultados do item (b).
(d) Se apenas um diodo estivesse presente, determine qual seria a corrente dele e compare com o valor máximo nominal.
(a) 30mA; (b) 26,81 mA; (c) 12,456 mA; (d) Seria 12,456 mA que é menor que 30 mA
(a) 30mA; (b) 26,81 mA; (c) 31,267 mA; (d) Seria 26,81 mA que é menor que 30 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 17,83 mA que é menor que 20 mA
(a) 10mA; (b) 0 mA; (c) 5 mA; (d) Seria 5 mA que é menor que 10 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 8,915 mA que é menor que 20 mA
Qual é o valor da tensão de saída (Vo), considerando que a tensão base-coletor (Vbco) é de 70V?

Vo = - 80V
vo = + 70V
Vo = + 80V
Vo = + 60V
Vo = - 60V
Considere as afirmações abaixo:
(1) O diodo semicondutor é formado pela união de dois materiais extrínsecos apresentados, um do tipo P e outro do tipo N.
(2) Após o processo de dopagem do semicondutor com uma impureza constituída de átomos trivalentes, o material passa a ser chamado de material tipo P.
(3) O diodo semicondutor não sofre os efeitos da temperatura, mantendo sua corrente na polarização direta e reversa sempre constante, de acordo com o ponto de operação.
(4) Na junção dos dois materiais existe uma região de depleção, formada pela combinação de elétrons e lacunas, oferecendo uma barreira de potencial elétrico de aproximadamente 0,7V para diodos de silício.
Diante das afirmações apresentadas acima, podemos classificar como verdadeiras:
Todas as afirmações.
As afirmações 2 e 4.
As afirmações 1 e 2.
As afirmações 1, 2 e 4.
As afirmações 1 e 4.
Na figura abaixo, é apresentado um gráfico mostrando uma condição de operação do diodo. Podemos descrever o parâmetro (Trr) como:

Tempo de acionamento de um diodo
Tempo de chaveamento ao ligar e desligar um diodo
Capacitância de transição do diodo
Tempo de recuperação reversa de um diodo
Resistência de corpo do diodo
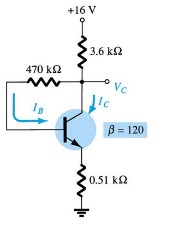
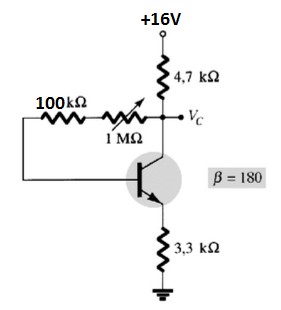
Determine a faixa de valores possíveis para Vc para o circuito da figura abaixo, utilizando o potenciômetro de 1 MOhm.

(I) 200; (II) 13,12V (III) 747 kOhm
(I) 105; (II) 17,74V (III) 747 kOhm
(I) 244; (II) 12,55V (III) 910 kOhm
(I) 154,4; (II) 15,11V (III) 565 kOhm
(I) 154,4; (II) 17,74V (III) 747 kOhm
Determine o valor de para cada circuito da figura abaixo.

(a) Vo = 0 V (b) Vo = 7,96 V
(a) Vo = 9,3 V (b) Vo = 7 V
(a) Vo = 9,5 V (b) Vo = 7,96 V
(a) Vo = 9,5 V (b) Vo = 7 V
(a) Vo = 0 V (b) Vo = 7 V
Para o circuito da figura abaixo:
(a) Vc aumenta ou diminui quando RB aumenta?
(b) IC aumenta ou diminui quando B é reduzido?
(c) O que acontece com a corrente de saturação quando B aumenta?
(d) A corrente do coletor aumenta ou diminui quando VCC é reduzida?
(e) O que acontece com VCE se o transistor é substituído por outro com B menor?

(a) RB aumenta, IB aumenta, IC diminui, VC aumenta; (b) Beta diminui, IC diminui; (c) diminui; (d) VCC aumenta, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC aumenta, VRE diminui, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC diminui; (b) Beta diminui, IC aumenta; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC diminui, VRE aumenta, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC aumenta; (b) Beta diminui, IC aumenta; (c) aumenta; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC aumenta, VRC diminui, VRE aumenta, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC aumenta; (b) Beta diminui, IC diminui; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC diminui, VRE diminui, VCE aumenta
(a) RB aumenta, IB diminui, IC aumenta, VC aumenta; (b) Beta diminui, IC aumenta; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC aumenta, VRC diminui, VRE diminui, VCE aumenta
Dado o circuito abaixo responda:
(a) Dado Pmáx = 14 mW para cada diodo da figura, determine a corrente máxima nominal de cada diodo (utilizando o modelo equivalente aproximado).
(b) Determine Imáx para Vimáx = 78 V.
(c) Determine a corrente através de cada diodo para Vimáx utilizando os resultados do item (b).
(d) Se apenas um diodo estivesse presente, determine qual seria a corrente dele e compare com o valor máximo nominal.

(a) 30mA; (b) 26,81 mA; (c) 12,456 mA; (d) Seria 12,456 mA que é menor que 30 mA
(a) 30mA; (b) 26,81 mA; (c) 31,267 mA; (d) Seria 26,81 mA que é menor que 30 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 17,83 mA que é menor que 20 mA
(a) 10mA; (b) 0 mA; (c) 5 mA; (d) Seria 5 mA que é menor que 10 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 8,915 mA que é menor que 20 mA
Qual é o valor da tensão de saída (Vo), considerando que a tensão base-coletor (Vbco) é de 70V?

Vo = - 80V
vo = + 70V
Vo = + 80V
Vo = + 60V
Vo = - 60V
Considere as afirmações abaixo:
(1) O diodo semicondutor é formado pela união de dois materiais extrínsecos apresentados, um do tipo P e outro do tipo N.
(2) Após o processo de dopagem do semicondutor com uma impureza constituída de átomos trivalentes, o material passa a ser chamado de material tipo P.
(3) O diodo semicondutor não sofre os efeitos da temperatura, mantendo sua corrente na polarização direta e reversa sempre constante, de acordo com o ponto de operação.
(4) Na junção dos dois materiais existe uma região de depleção, formada pela combinação de elétrons e lacunas, oferecendo uma barreira de potencial elétrico de aproximadamente 0,7V para diodos de silício.
Diante das afirmações apresentadas acima, podemos classificar como verdadeiras:
Todas as afirmações.
As afirmações 2 e 4.
As afirmações 1 e 2.
As afirmações 1, 2 e 4.
As afirmações 1 e 4.
Na figura abaixo, é apresentado um gráfico mostrando uma condição de operação do diodo. Podemos descrever o parâmetro (Trr) como:

Tempo de acionamento de um diodo
Tempo de chaveamento ao ligar e desligar um diodo
Capacitância de transição do diodo
Tempo de recuperação reversa de um diodo
Resistência de corpo do diodo
Determine a faixa de valores possíveis para Vc para o circuito da figura abaixo, utilizando o potenciômetro de 1 MOhm.


(a) Vo = 0 V (b) Vo = 7,96 V
(a) Vo = 9,3 V (b) Vo = 7 V
(a) Vo = 9,5 V (b) Vo = 7,96 V
(a) Vo = 9,5 V (b) Vo = 7 V
(a) Vo = 0 V (b) Vo = 7 V
Para o circuito da figura abaixo:
(a) Vc aumenta ou diminui quando RB aumenta?
(b) IC aumenta ou diminui quando B é reduzido?
(c) O que acontece com a corrente de saturação quando B aumenta?
(d) A corrente do coletor aumenta ou diminui quando VCC é reduzida?
(e) O que acontece com VCE se o transistor é substituído por outro com B menor?

(a) RB aumenta, IB aumenta, IC diminui, VC aumenta; (b) Beta diminui, IC diminui; (c) diminui; (d) VCC aumenta, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC aumenta, VRE diminui, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC diminui; (b) Beta diminui, IC aumenta; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC diminui, VRE aumenta, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC aumenta; (b) Beta diminui, IC aumenta; (c) aumenta; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC aumenta, VRC diminui, VRE aumenta, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC aumenta; (b) Beta diminui, IC diminui; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC diminui, VRE diminui, VCE aumenta
(a) RB aumenta, IB diminui, IC aumenta, VC aumenta; (b) Beta diminui, IC aumenta; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC aumenta, VRC diminui, VRE diminui, VCE aumenta
Dado o circuito abaixo responda:
(a) Dado Pmáx = 14 mW para cada diodo da figura, determine a corrente máxima nominal de cada diodo (utilizando o modelo equivalente aproximado).
(b) Determine Imáx para Vimáx = 78 V.
(c) Determine a corrente através de cada diodo para Vimáx utilizando os resultados do item (b).
(d) Se apenas um diodo estivesse presente, determine qual seria a corrente dele e compare com o valor máximo nominal.

(a) 30mA; (b) 26,81 mA; (c) 12,456 mA; (d) Seria 12,456 mA que é menor que 30 mA
(a) 30mA; (b) 26,81 mA; (c) 31,267 mA; (d) Seria 26,81 mA que é menor que 30 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 17,83 mA que é menor que 20 mA
(a) 10mA; (b) 0 mA; (c) 5 mA; (d) Seria 5 mA que é menor que 10 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 8,915 mA que é menor que 20 mA
Qual é o valor da tensão de saída (Vo), considerando que a tensão base-coletor (Vbco) é de 70V?

Vo = - 80V
vo = + 70V
Vo = + 80V
Vo = + 60V
Vo = - 60V
Considere as afirmações abaixo:
(1) O diodo semicondutor é formado pela união de dois materiais extrínsecos apresentados, um do tipo P e outro do tipo N.
(2) Após o processo de dopagem do semicondutor com uma impureza constituída de átomos trivalentes, o material passa a ser chamado de material tipo P.
(3) O diodo semicondutor não sofre os efeitos da temperatura, mantendo sua corrente na polarização direta e reversa sempre constante, de acordo com o ponto de operação.
(4) Na junção dos dois materiais existe uma região de depleção, formada pela combinação de elétrons e lacunas, oferecendo uma barreira de potencial elétrico de aproximadamente 0,7V para diodos de silício.
Diante das afirmações apresentadas acima, podemos classificar como verdadeiras:
Todas as afirmações.
As afirmações 2 e 4.
As afirmações 1 e 2.
As afirmações 1, 2 e 4.
As afirmações 1 e 4.
Na figura abaixo, é apresentado um gráfico mostrando uma condição de operação do diodo. Podemos descrever o parâmetro (Trr) como:

Tempo de acionamento de um diodo
Tempo de chaveamento ao ligar e desligar um diodo
Capacitância de transição do diodo
Tempo de recuperação reversa de um diodo
Resistência de corpo do diodo
Determine a faixa de valores possíveis para Vc para o circuito da figura abaixo, utilizando o potenciômetro de 1 MOhm.


(a) RB aumenta, IB aumenta, IC diminui, VC aumenta; (b) Beta diminui, IC diminui; (c) diminui; (d) VCC aumenta, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC aumenta, VRE diminui, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC diminui; (b) Beta diminui, IC aumenta; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC diminui, VRE aumenta, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC aumenta; (b) Beta diminui, IC aumenta; (c) aumenta; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC aumenta, VRC diminui, VRE aumenta, VCE aumenta
(a) RB aumenta, IB diminui, IC diminui, VC aumenta; (b) Beta diminui, IC diminui; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC diminui, VRC diminui, VRE diminui, VCE aumenta
(a) RB aumenta, IB diminui, IC aumenta, VC aumenta; (b) Beta diminui, IC aumenta; (c) Inalterado; (d) VCC diminui, IB diminui, IC diminui; (e) Beta diminui, IC aumenta, VRC diminui, VRE diminui, VCE aumenta
Dado o circuito abaixo responda:
(a) Dado Pmáx = 14 mW para cada diodo da figura, determine a corrente máxima nominal de cada diodo (utilizando o modelo equivalente aproximado).
(b) Determine Imáx para Vimáx = 78 V.
(c) Determine a corrente através de cada diodo para Vimáx utilizando os resultados do item (b).
(d) Se apenas um diodo estivesse presente, determine qual seria a corrente dele e compare com o valor máximo nominal.

(a) 30mA; (b) 26,81 mA; (c) 12,456 mA; (d) Seria 12,456 mA que é menor que 30 mA
(a) 30mA; (b) 26,81 mA; (c) 31,267 mA; (d) Seria 26,81 mA que é menor que 30 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 17,83 mA que é menor que 20 mA
(a) 10mA; (b) 0 mA; (c) 5 mA; (d) Seria 5 mA que é menor que 10 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 8,915 mA que é menor que 20 mA
Qual é o valor da tensão de saída (Vo), considerando que a tensão base-coletor (Vbco) é de 70V?

Vo = - 80V
vo = + 70V
Vo = + 80V
Vo = + 60V
Vo = - 60V
Considere as afirmações abaixo:
(1) O diodo semicondutor é formado pela união de dois materiais extrínsecos apresentados, um do tipo P e outro do tipo N.
(2) Após o processo de dopagem do semicondutor com uma impureza constituída de átomos trivalentes, o material passa a ser chamado de material tipo P.
(3) O diodo semicondutor não sofre os efeitos da temperatura, mantendo sua corrente na polarização direta e reversa sempre constante, de acordo com o ponto de operação.
(4) Na junção dos dois materiais existe uma região de depleção, formada pela combinação de elétrons e lacunas, oferecendo uma barreira de potencial elétrico de aproximadamente 0,7V para diodos de silício.
Diante das afirmações apresentadas acima, podemos classificar como verdadeiras:
Todas as afirmações.
As afirmações 2 e 4.
As afirmações 1 e 2.
As afirmações 1, 2 e 4.
As afirmações 1 e 4.
Na figura abaixo, é apresentado um gráfico mostrando uma condição de operação do diodo. Podemos descrever o parâmetro (Trr) como:

Tempo de acionamento de um diodo
Tempo de chaveamento ao ligar e desligar um diodo
Capacitância de transição do diodo
Tempo de recuperação reversa de um diodo
Resistência de corpo do diodo
Determine a faixa de valores possíveis para Vc para o circuito da figura abaixo, utilizando o potenciômetro de 1 MOhm.


(a) 30mA; (b) 26,81 mA; (c) 12,456 mA; (d) Seria 12,456 mA que é menor que 30 mA
(a) 30mA; (b) 26,81 mA; (c) 31,267 mA; (d) Seria 26,81 mA que é menor que 30 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 17,83 mA que é menor que 20 mA
(a) 10mA; (b) 0 mA; (c) 5 mA; (d) Seria 5 mA que é menor que 10 mA
(a) 20mA; (b) 17,83 mA; (c) 8,915 mA; (d) Seria 8,915 mA que é menor que 20 mA
Qual é o valor da tensão de saída (Vo), considerando que a tensão base-coletor (Vbco) é de 70V?

Vo = - 80V
vo = + 70V
Vo = + 80V
Vo = + 60V
Vo = - 60V
Considere as afirmações abaixo:
(1) O diodo semicondutor é formado pela união de dois materiais extrínsecos apresentados, um do tipo P e outro do tipo N.
(2) Após o processo de dopagem do semicondutor com uma impureza constituída de átomos trivalentes, o material passa a ser chamado de material tipo P.
(3) O diodo semicondutor não sofre os efeitos da temperatura, mantendo sua corrente na polarização direta e reversa sempre constante, de acordo com o ponto de operação.
(4) Na junção dos dois materiais existe uma região de depleção, formada pela combinação de elétrons e lacunas, oferecendo uma barreira de potencial elétrico de aproximadamente 0,7V para diodos de silício.
Diante das afirmações apresentadas acima, podemos classificar como verdadeiras:
Todas as afirmações.
As afirmações 2 e 4.
As afirmações 1 e 2.
As afirmações 1, 2 e 4.
As afirmações 1 e 4.
Na figura abaixo, é apresentado um gráfico mostrando uma condição de operação do diodo. Podemos descrever o parâmetro (Trr) como:

Tempo de acionamento de um diodo
Tempo de chaveamento ao ligar e desligar um diodo
Capacitância de transição do diodo
Tempo de recuperação reversa de um diodo
Resistência de corpo do diodo
Determine a faixa de valores possíveis para Vc para o circuito da figura abaixo, utilizando o potenciômetro de 1 MOhm.

Vo = - 80V
vo = + 70V
Vo = + 80V
Vo = + 60V
Vo = - 60V
Considere as afirmações abaixo:
(1) O diodo semicondutor é formado pela união de dois materiais extrínsecos apresentados, um do tipo P e outro do tipo N.
(2) Após o processo de dopagem do semicondutor com uma impureza constituída de átomos trivalentes, o material passa a ser chamado de material tipo P.
(3) O diodo semicondutor não sofre os efeitos da temperatura, mantendo sua corrente na polarização direta e reversa sempre constante, de acordo com o ponto de operação.
(4) Na junção dos dois materiais existe uma região de depleção, formada pela combinação de elétrons e lacunas, oferecendo uma barreira de potencial elétrico de aproximadamente 0,7V para diodos de silício.
Diante das afirmações apresentadas acima, podemos classificar como verdadeiras:
Todas as afirmações.
As afirmações 2 e 4.
As afirmações 1 e 2.
As afirmações 1, 2 e 4.
As afirmações 1 e 4.
Na figura abaixo, é apresentado um gráfico mostrando uma condição de operação do diodo. Podemos descrever o parâmetro (Trr) como:

Tempo de acionamento de um diodo
Tempo de chaveamento ao ligar e desligar um diodo
Capacitância de transição do diodo
Tempo de recuperação reversa de um diodo
Resistência de corpo do diodo
Determine a faixa de valores possíveis para Vc para o circuito da figura abaixo, utilizando o potenciômetro de 1 MOhm.

Todas as afirmações.
As afirmações 2 e 4.
As afirmações 1 e 2.
As afirmações 1, 2 e 4.
As afirmações 1 e 4.
Na figura abaixo, é apresentado um gráfico mostrando uma condição de operação do diodo. Podemos descrever o parâmetro (Trr) como:

Tempo de acionamento de um diodo
Tempo de chaveamento ao ligar e desligar um diodo
Capacitância de transição do diodo
Tempo de recuperação reversa de um diodo
Resistência de corpo do diodo
Determine a faixa de valores possíveis para Vc para o circuito da figura abaixo, utilizando o potenciômetro de 1 MOhm.

Tempo de acionamento de um diodo
Tempo de chaveamento ao ligar e desligar um diodo
Capacitância de transição do diodo
Tempo de recuperação reversa de um diodo
Resistência de corpo do diodo
Determine a faixa de valores possíveis para Vc para o circuito da figura abaixo, utilizando o potenciômetro de 1 MOhm.