CÁLCULO IV
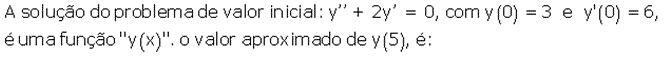
5,0
4,5
6,8
5,5
6,0

abril de 2008
fevereiro de 2008
agosto de 2008
outubro de 2008
dezembro de 2007
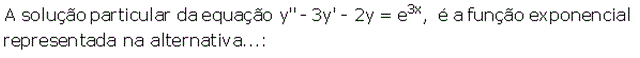
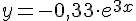
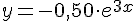
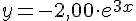
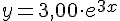
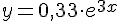

V V F F
V V V F
V F F F
V F V F
V F F V
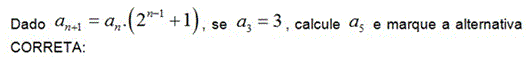

Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da convergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Não vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a um e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.

5,0
4,5
6,8
5,5
6,0

abril de 2008
fevereiro de 2008
agosto de 2008
outubro de 2008
dezembro de 2007
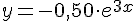
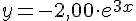
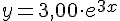
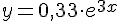

V V F F
V V V F
V F F F
V F V F
V F F V
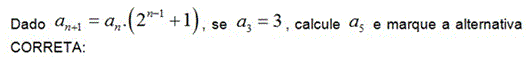
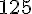
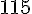
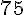

Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da convergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Não vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a um e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.

abril de 2008
fevereiro de 2008
agosto de 2008
outubro de 2008
dezembro de 2007
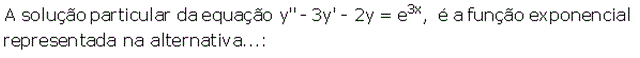
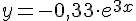
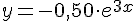
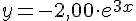
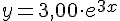
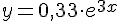

V V F F
V V V F
V F F F
V F V F
V F F V
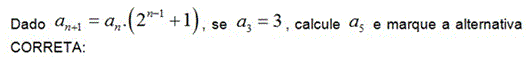
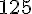
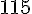
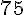

Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da convergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Não vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a um e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.

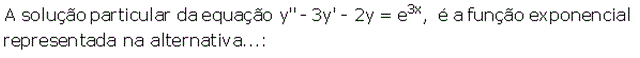

V V F F
V V V F
V F F F
V F V F
V F F V
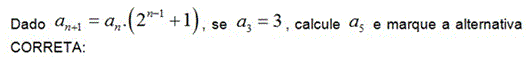

Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da convergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Não vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a um e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.


V V F F
V V V F
V F F F
V F V F
V F F V
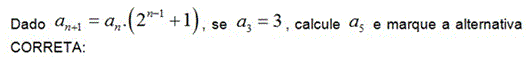
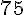
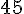
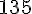

Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da convergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Não vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a um e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.

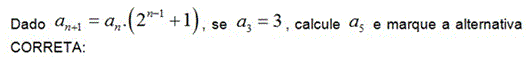

Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da convergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Não vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a um e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.


Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da convergência.
Existem séries cujo termo genérico tende a zero e que não são convergentes. Não vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.
Existem séries cujo termo genérico tende a um e que não são convergentes. Vale a contra positiva: "se o limite não é zero, então a série não converge", que constitui o teste da divergência.


