CÁLCULO I
Ao resolver o limite  , utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será? Assinale a alternativa CORRETA.
, utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será? Assinale a alternativa CORRETA.
não existe
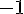
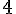


Dada a função %7D%7D%7D) , determine a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
, determine a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
%7D%7D%5E%7B%7B2%7D%7D%7D)
%7D%7D%5E%7B%7B2%7D%7D%7D)
%7D%7D%5E%7B%7B2%7D%7D%7D)

%7D%7D%5E%7B%7B2%7D%7D%7D)
Determine a derivada primeira da função da função expressa por %7D%7D%7D%3D%7B40%7D-%5Cfrac%7B%7B%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B3%7D%7D%7D%7D%7B%7B%7B3%7D%7D%7D-%5Cfrac%7B%7B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%7D%7D%7B%7B%7B4%7D%7D%7D) e, em seguida, assinale a alternativa CORRETA.
e, em seguida, assinale a alternativa CORRETA.
%7D%3D-%7B24%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B2%7D%7Bx%7D)
%7D%3D%7B40%7D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7Bx%7D%7D%7D%7B%7B%7B2%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7B4%7D%7Bx%7D%7D%7D%7B%7B%7B3%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7B8%7D%7Bx%7D%7D%7D%7B%7B%7B3%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7Bx%7D%7D%7D%7B%7B%7B2%7D%7D%7D)
O valor CORRETO para o cálculo do limite %7D%7D%7D%7B%7B%7B%5Cleft(%7B17%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B58%7D%7Bx%7D%2B%7B61%7D%5Cright)%7D%7D%7D) corresponde EXATAMENTE a:
corresponde EXATAMENTE a:
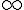

0 (zero)
não existe

Seja dada a função %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B1%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3C%7B2%7D%5C%5C%7B2%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3D%7B2%7D%5C%5C%7B9%7D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3E%7B2%7D%7D%5Cright.%7D) , determine o limite
, determine o limite %7D%7D%7D) , analise o gráfico, e em seguida assinale a alternativa CORRETA.
, analise o gráfico, e em seguida assinale a alternativa CORRETA.
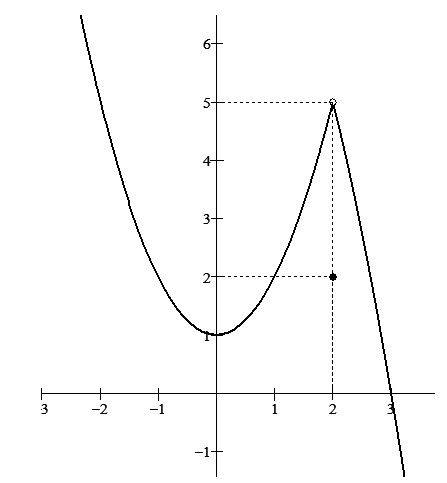
O limite no ponto de tendência x=2 existe e é igual a 5, mas a função é descontínua neste ponto, pois o ponto (2,5) não pertence à função.
O limite no ponto de tendência x=2 existe e é igual a 5, logo a função é contínua neste ponto.
O limite no ponto de tendência x=2 não existe, logo a função é descontínua neste ponto.
O limite no ponto de tendência x=2 existe e é igual a 5, e a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
O limite no ponto de tendência x=2 não existe, mas a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
Dada a função  , encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
, encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
não existe
Dada a função %7D%7D%7D) , determine a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
, determine a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
%7D%7D%5E%7B%7B2%7D%7D%7D)
%7D%7D%5E%7B%7B2%7D%7D%7D)
%7D%7D%5E%7B%7B2%7D%7D%7D)

%7D%7D%5E%7B%7B2%7D%7D%7D)
Determine a derivada primeira da função da função expressa por %7D%7D%7D%3D%7B40%7D-%5Cfrac%7B%7B%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B3%7D%7D%7D%7D%7B%7B%7B3%7D%7D%7D-%5Cfrac%7B%7B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%7D%7D%7B%7B%7B4%7D%7D%7D) e, em seguida, assinale a alternativa CORRETA.
e, em seguida, assinale a alternativa CORRETA.
%7D%3D-%7B24%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B2%7D%7Bx%7D)
%7D%3D%7B40%7D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7Bx%7D%7D%7D%7B%7B%7B2%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7B4%7D%7Bx%7D%7D%7D%7B%7B%7B3%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7B8%7D%7Bx%7D%7D%7D%7B%7B%7B3%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7Bx%7D%7D%7D%7B%7B%7B2%7D%7D%7D)
O valor CORRETO para o cálculo do limite %7D%7D%7D%7B%7B%7B%5Cleft(%7B17%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B58%7D%7Bx%7D%2B%7B61%7D%5Cright)%7D%7D%7D) corresponde EXATAMENTE a:
corresponde EXATAMENTE a:
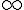

0 (zero)
não existe

Seja dada a função %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B1%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3C%7B2%7D%5C%5C%7B2%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3D%7B2%7D%5C%5C%7B9%7D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3E%7B2%7D%7D%5Cright.%7D) , determine o limite
, determine o limite %7D%7D%7D) , analise o gráfico, e em seguida assinale a alternativa CORRETA.
, analise o gráfico, e em seguida assinale a alternativa CORRETA.

O limite no ponto de tendência x=2 existe e é igual a 5, mas a função é descontínua neste ponto, pois o ponto (2,5) não pertence à função.
O limite no ponto de tendência x=2 existe e é igual a 5, logo a função é contínua neste ponto.
O limite no ponto de tendência x=2 não existe, logo a função é descontínua neste ponto.
O limite no ponto de tendência x=2 existe e é igual a 5, e a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
O limite no ponto de tendência x=2 não existe, mas a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
Dada a função  , encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
, encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
Determine a derivada primeira da função da função expressa por %7D%7D%7D%3D%7B40%7D-%5Cfrac%7B%7B%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B3%7D%7D%7D%7D%7B%7B%7B3%7D%7D%7D-%5Cfrac%7B%7B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%7D%7D%7B%7B%7B4%7D%7D%7D) e, em seguida, assinale a alternativa CORRETA.
e, em seguida, assinale a alternativa CORRETA.
%7D%3D-%7B24%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7B2%7D%7Bx%7D)
%7D%3D%7B40%7D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7Bx%7D%7D%7D%7B%7B%7B2%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7B4%7D%7Bx%7D%7D%7D%7B%7B%7B3%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7B8%7D%7Bx%7D%7D%7D%7B%7B%7B3%7D%7D%7D)
%7D%3D-%7B8%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%5Cfrac%7B%7B%7Bx%7D%7D%7D%7B%7B%7B2%7D%7D%7D)
O valor CORRETO para o cálculo do limite %7D%7D%7D%7B%7B%7B%5Cleft(%7B17%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B58%7D%7Bx%7D%2B%7B61%7D%5Cright)%7D%7D%7D) corresponde EXATAMENTE a:
corresponde EXATAMENTE a:
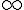

0 (zero)
não existe

Seja dada a função %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B1%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3C%7B2%7D%5C%5C%7B2%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3D%7B2%7D%5C%5C%7B9%7D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3E%7B2%7D%7D%5Cright.%7D) , determine o limite
, determine o limite %7D%7D%7D) , analise o gráfico, e em seguida assinale a alternativa CORRETA.
, analise o gráfico, e em seguida assinale a alternativa CORRETA.

O limite no ponto de tendência x=2 existe e é igual a 5, mas a função é descontínua neste ponto, pois o ponto (2,5) não pertence à função.
O limite no ponto de tendência x=2 existe e é igual a 5, logo a função é contínua neste ponto.
O limite no ponto de tendência x=2 não existe, logo a função é descontínua neste ponto.
O limite no ponto de tendência x=2 existe e é igual a 5, e a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
O limite no ponto de tendência x=2 não existe, mas a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
Dada a função  , encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
, encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
O valor CORRETO para o cálculo do limite %7D%7D%7D%7B%7B%7B%5Cleft(%7B17%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B58%7D%7Bx%7D%2B%7B61%7D%5Cright)%7D%7D%7D) corresponde EXATAMENTE a:
corresponde EXATAMENTE a:
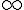

0 (zero)
não existe

Seja dada a função %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B1%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3C%7B2%7D%5C%5C%7B2%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3D%7B2%7D%5C%5C%7B9%7D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3E%7B2%7D%7D%5Cright.%7D) , determine o limite
, determine o limite %7D%7D%7D) , analise o gráfico, e em seguida assinale a alternativa CORRETA.
, analise o gráfico, e em seguida assinale a alternativa CORRETA.

O limite no ponto de tendência x=2 existe e é igual a 5, mas a função é descontínua neste ponto, pois o ponto (2,5) não pertence à função.
O limite no ponto de tendência x=2 existe e é igual a 5, logo a função é contínua neste ponto.
O limite no ponto de tendência x=2 não existe, logo a função é descontínua neste ponto.
O limite no ponto de tendência x=2 existe e é igual a 5, e a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
O limite no ponto de tendência x=2 não existe, mas a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
Dada a função  , encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
, encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
0 (zero)
não existe
Seja dada a função %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B1%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3C%7B2%7D%5C%5C%7B2%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3D%7B2%7D%5C%5C%7B9%7D-%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%26%7Bp%7D%7Ba%7D%7Br%7D%7Ba%7D%7Bx%7D%3E%7B2%7D%7D%5Cright.%7D) , determine o limite
, determine o limite %7D%7D%7D) , analise o gráfico, e em seguida assinale a alternativa CORRETA.
, analise o gráfico, e em seguida assinale a alternativa CORRETA.

O limite no ponto de tendência x=2 existe e é igual a 5, mas a função é descontínua neste ponto, pois o ponto (2,5) não pertence à função.
O limite no ponto de tendência x=2 existe e é igual a 5, logo a função é contínua neste ponto.
O limite no ponto de tendência x=2 não existe, logo a função é descontínua neste ponto.
O limite no ponto de tendência x=2 existe e é igual a 5, e a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
O limite no ponto de tendência x=2 não existe, mas a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
Dada a função  , encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.
, encontre a sua SEGUNDA derivada e, em seguida, assinale a alternativa CORRETA.

O limite no ponto de tendência x=2 existe e é igual a 5, mas a função é descontínua neste ponto, pois o ponto (2,5) não pertence à função.
O limite no ponto de tendência x=2 existe e é igual a 5, logo a função é contínua neste ponto.
O limite no ponto de tendência x=2 não existe, logo a função é descontínua neste ponto.
O limite no ponto de tendência x=2 existe e é igual a 5, e a função é contínua neste ponto, pois o ponto (2,5) pertence à função.
O limite no ponto de tendência x=2 não existe, mas a função é contínua neste ponto, pois o ponto (2,5) pertence à função.