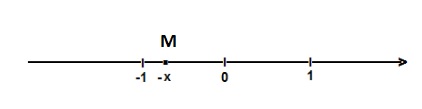TEORIA DOS NÚMEROS II
Nesta reta numérica, estão representados os números racionais 

Os pontos que correspondem aos números  são, respectivamente,
são, respectivamente,
M, Q, P,N
N, Q, P,M
Q, P, M, N
Q, M, P,N
N, M, P, Q
Obtenha o valor de k que satisfaz a condição, onde Z que deve ser um número real. Sabendo que 
k = 5
k = 2
k = -1


De acordo com o conjunto dos números inteiros, observe as afirmativa a seguir: 
Julgando-as como verdadeiras ou falsas, obtemos a seguinte sequência correta:
F V F F
V F V V
V F V F
F V F V
F V V F
O valor da expressão i10 + i11 + i12 + i13 é igual a:
-i
0
-i + 1
i
-1
De acordo com os seus estudos. os números que são usados rotineiramente em nossas vidas são chamados, números reais. Esses números são divididos em diversos conjuntos, cada qual com uma origem e um emprego específico, sendo assim leia as afirmativas a seguir:
I.Todo número natural é real.
II. Todo número real é racional.
III. Todo número racional pode ser escrito como uma fração na qual o numerador e o denominador são naturais.
IV.Todo número irracional é real.
V.Todo número inteiro é natural.
Pode se afirmar que:
Apenas II, III e IV
Apenas III e IV
Apenas I, II e III
Apenas I e III
Apenas I e IV
Leia as três afirmativas a seguir:
I. 3/8 de 72 = 27
II. 10% de 8000 = 800
III. 1% de 7000 = 700
É(São) verdadeira(s) a(s) afirmação(ões):
I e II, somente
II, somente
I, somente
I e III, somente
II e III somente
A divisão de números fracionários está ligada a ideia de verificar quantos cabem. Com base nesta afirmação responda a pergunta:
Quantos 1/4 cabem em 5 inteiros?
5: 1/4 = 19
5: 1/4 = 21
5: 1/4 = 20
5: 1/4 =5/4
5: 1/4 = 5
Dados os números complexos Z1 =(2 - y, y) e Z2= (x, 2) . Sabendo que x e y são números reais e que Z2 - Z1 = (7, 4), pode-se afirmar que o valor de x e y valem, respectivamente:
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
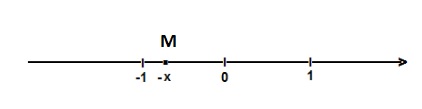
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :
Os pontos que correspondem aos números
M, Q, P,N
N, Q, P,M
Q, P, M, N
Q, M, P,N
N, M, P, Q
Obtenha o valor de k que satisfaz a condição, onde Z que deve ser um número real. Sabendo que 
k = 5
k = 2
k = -1


De acordo com o conjunto dos números inteiros, observe as afirmativa a seguir: 
Julgando-as como verdadeiras ou falsas, obtemos a seguinte sequência correta:
F V F F
V F V V
V F V F
F V F V
F V V F
O valor da expressão i10 + i11 + i12 + i13 é igual a:
-i
0
-i + 1
i
-1
De acordo com os seus estudos. os números que são usados rotineiramente em nossas vidas são chamados, números reais. Esses números são divididos em diversos conjuntos, cada qual com uma origem e um emprego específico, sendo assim leia as afirmativas a seguir:
I.Todo número natural é real.
II. Todo número real é racional.
III. Todo número racional pode ser escrito como uma fração na qual o numerador e o denominador são naturais.
IV.Todo número irracional é real.
V.Todo número inteiro é natural.
Pode se afirmar que:
Apenas II, III e IV
Apenas III e IV
Apenas I, II e III
Apenas I e III
Apenas I e IV
Leia as três afirmativas a seguir:
I. 3/8 de 72 = 27
II. 10% de 8000 = 800
III. 1% de 7000 = 700
É(São) verdadeira(s) a(s) afirmação(ões):
I e II, somente
II, somente
I, somente
I e III, somente
II e III somente
A divisão de números fracionários está ligada a ideia de verificar quantos cabem. Com base nesta afirmação responda a pergunta:
Quantos 1/4 cabem em 5 inteiros?

5: 1/4 = 19
5: 1/4 = 21
5: 1/4 = 20
5: 1/4 =5/4
5: 1/4 = 5
Dados os números complexos Z1 =(2 - y, y) e Z2= (x, 2) . Sabendo que x e y são números reais e que Z2 - Z1 = (7, 4), pode-se afirmar que o valor de x e y valem, respectivamente:
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
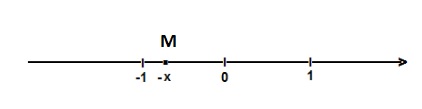
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :
k = 5
k = 2
k = -1
De acordo com o conjunto dos números inteiros, observe as afirmativa a seguir: 
Julgando-as como verdadeiras ou falsas, obtemos a seguinte sequência correta:
F V F F
V F V V
V F V F
F V F V
F V V F
O valor da expressão i10 + i11 + i12 + i13 é igual a:
-i
0
-i + 1
i
-1
De acordo com os seus estudos. os números que são usados rotineiramente em nossas vidas são chamados, números reais. Esses números são divididos em diversos conjuntos, cada qual com uma origem e um emprego específico, sendo assim leia as afirmativas a seguir:
I.Todo número natural é real.
II. Todo número real é racional.
III. Todo número racional pode ser escrito como uma fração na qual o numerador e o denominador são naturais.
IV.Todo número irracional é real.
V.Todo número inteiro é natural.
Pode se afirmar que:
Apenas II, III e IV
Apenas III e IV
Apenas I, II e III
Apenas I e III
Apenas I e IV
Leia as três afirmativas a seguir:
I. 3/8 de 72 = 27
II. 10% de 8000 = 800
III. 1% de 7000 = 700
É(São) verdadeira(s) a(s) afirmação(ões):
I e II, somente
II, somente
I, somente
I e III, somente
II e III somente
A divisão de números fracionários está ligada a ideia de verificar quantos cabem. Com base nesta afirmação responda a pergunta:
Quantos 1/4 cabem em 5 inteiros?

5: 1/4 = 19
5: 1/4 = 21
5: 1/4 = 20
5: 1/4 =5/4
5: 1/4 = 5
Dados os números complexos Z1 =(2 - y, y) e Z2= (x, 2) . Sabendo que x e y são números reais e que Z2 - Z1 = (7, 4), pode-se afirmar que o valor de x e y valem, respectivamente:
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
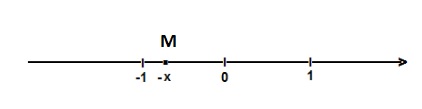
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :
F V F F
V F V V
V F V F
F V F V
F V V F
O valor da expressão i10 + i11 + i12 + i13 é igual a:
-i
0
-i + 1
i
-1
De acordo com os seus estudos. os números que são usados rotineiramente em nossas vidas são chamados, números reais. Esses números são divididos em diversos conjuntos, cada qual com uma origem e um emprego específico, sendo assim leia as afirmativas a seguir:
I.Todo número natural é real.
II. Todo número real é racional.
III. Todo número racional pode ser escrito como uma fração na qual o numerador e o denominador são naturais.
IV.Todo número irracional é real.
V.Todo número inteiro é natural.
Pode se afirmar que:
Apenas II, III e IV
Apenas III e IV
Apenas I, II e III
Apenas I e III
Apenas I e IV
Leia as três afirmativas a seguir:
I. 3/8 de 72 = 27
II. 10% de 8000 = 800
III. 1% de 7000 = 700
É(São) verdadeira(s) a(s) afirmação(ões):
I e II, somente
II, somente
I, somente
I e III, somente
II e III somente
A divisão de números fracionários está ligada a ideia de verificar quantos cabem. Com base nesta afirmação responda a pergunta:
Quantos 1/4 cabem em 5 inteiros?

5: 1/4 = 19
5: 1/4 = 21
5: 1/4 = 20
5: 1/4 =5/4
5: 1/4 = 5
Dados os números complexos Z1 =(2 - y, y) e Z2= (x, 2) . Sabendo que x e y são números reais e que Z2 - Z1 = (7, 4), pode-se afirmar que o valor de x e y valem, respectivamente:
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
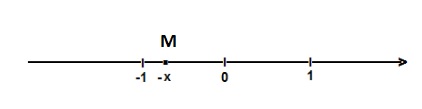
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :
-i
0
-i + 1
i
-1
De acordo com os seus estudos. os números que são usados rotineiramente em nossas vidas são chamados, números reais. Esses números são divididos em diversos conjuntos, cada qual com uma origem e um emprego específico, sendo assim leia as afirmativas a seguir:
I.Todo número natural é real.
II. Todo número real é racional.
III. Todo número racional pode ser escrito como uma fração na qual o numerador e o denominador são naturais.
IV.Todo número irracional é real.
V.Todo número inteiro é natural.
Pode se afirmar que:
Apenas II, III e IV
Apenas III e IV
Apenas I, II e III
Apenas I e III
Apenas I e IV
Leia as três afirmativas a seguir:
I. 3/8 de 72 = 27
II. 10% de 8000 = 800
III. 1% de 7000 = 700
É(São) verdadeira(s) a(s) afirmação(ões):
I e II, somente
II, somente
I, somente
I e III, somente
II e III somente
A divisão de números fracionários está ligada a ideia de verificar quantos cabem. Com base nesta afirmação responda a pergunta:
Quantos 1/4 cabem em 5 inteiros?

5: 1/4 = 19
5: 1/4 = 21
5: 1/4 = 20
5: 1/4 =5/4
5: 1/4 = 5
Dados os números complexos Z1 =(2 - y, y) e Z2= (x, 2) . Sabendo que x e y são números reais e que Z2 - Z1 = (7, 4), pode-se afirmar que o valor de x e y valem, respectivamente:
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
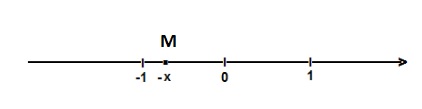
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :
Apenas II, III e IV
Apenas III e IV
Apenas I, II e III
Apenas I e III
Apenas I e IV
Leia as três afirmativas a seguir:
I. 3/8 de 72 = 27
II. 10% de 8000 = 800
III. 1% de 7000 = 700
É(São) verdadeira(s) a(s) afirmação(ões):
I e II, somente
II, somente
I, somente
I e III, somente
II e III somente
A divisão de números fracionários está ligada a ideia de verificar quantos cabem. Com base nesta afirmação responda a pergunta:
Quantos 1/4 cabem em 5 inteiros?

5: 1/4 = 19
5: 1/4 = 21
5: 1/4 = 20
5: 1/4 =5/4
5: 1/4 = 5
Dados os números complexos Z1 =(2 - y, y) e Z2= (x, 2) . Sabendo que x e y são números reais e que Z2 - Z1 = (7, 4), pode-se afirmar que o valor de x e y valem, respectivamente:
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
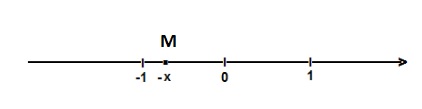
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :
I e II, somente
II, somente
I, somente
I e III, somente
II e III somente
A divisão de números fracionários está ligada a ideia de verificar quantos cabem. Com base nesta afirmação responda a pergunta:
Quantos 1/4 cabem em 5 inteiros?

5: 1/4 = 19
5: 1/4 = 21
5: 1/4 = 20
5: 1/4 =5/4
5: 1/4 = 5
Dados os números complexos Z1 =(2 - y, y) e Z2= (x, 2) . Sabendo que x e y são números reais e que Z2 - Z1 = (7, 4), pode-se afirmar que o valor de x e y valem, respectivamente:
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
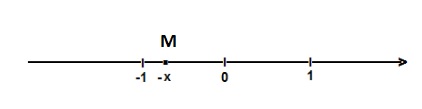
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :

5: 1/4 = 19
5: 1/4 = 21
5: 1/4 = 20
5: 1/4 =5/4
5: 1/4 = 5
Dados os números complexos Z1 =(2 - y, y) e Z2= (x, 2) . Sabendo que x e y são números reais e que Z2 - Z1 = (7, 4), pode-se afirmar que o valor de x e y valem, respectivamente:
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
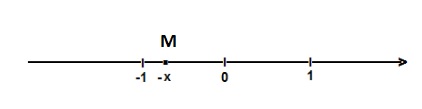
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :
11 e -2
7 e 2
-1 e -3
-2 e 11
2 e 7
Na reta numérica, está representada o ponto M de coordenada -x.
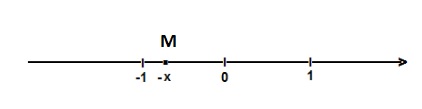
O ponto M que representa o número  , está representado nessa reta :
, está representado nessa reta :