TEORIA DOS NÚMEROS I
Para converter o número 1000102 para a base decimal siga os passos abaixo:
1° Passo: Inverter o número para fazermos a somatória da direita para a esquerda do número original.
100010 -> 010001
2° Passo: Somar cada número, multiplicando por 2 elevado a um número sequencial iniciado em 0.
0.20 + 1.21 + 0.22 + 0.23 + 0.24 + 1. 25
3° Passo: Calcular.
0 + 2 + 0 + 0 + 0 + 32 = 34
Logo o número1000102 é igual a 34 na base 10.
Seguindo o exposto acima, o número binário 1100101 na base 10 é igual a:
132
131
48
89
101
Duas composições de metrô de Uberinha partem simultaneamente de um mesmo terminal fazendo itinerários diferentes. Uma torna a partir do terminal a cada 80 minutos; a outra a cada hora e meia. Qual é o tempo percorrido entre duas partidas simultâneas consecutivas do termina?
15 horas
10 horas
20 horas
12 horas
15 horas
Pelo algoritmo de Euclides podemos afirmar que o MDC(54,70) é igual ao:
MDC(4,5)
MDC(22,4)
MDC (70,3)
MDC(12,3)
MDC(3,5)
Considere os números A e B, estão transcritos no sistema binário, sendo A = (10101) e B = (11010) , transcrevendo-os para o sistema de numeração de base 10 , o valor de B - A é igual a:
7
6
5
12
10
Dividimos sucessivamente o número da base decimal por 8 até que não seja mais divisível, ao final, o número na base octal é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter 2834 para a base 8.
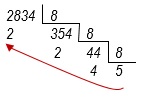
Ou seja 2834 = 5422 8 .
Seguindo o exposto acima, é correto afirmar que a conversão do número 3564 da base decimal para a base octal é exatamente:
6457 8
6834 8
6750 8
6725 8
6754 8
A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se pode realizar entre eles. Sabe-se que operar implica agir sobre um objeto ou sobre uma situação, realizar transformações e obter um efeito ou um resultado, então leia os itens a seguir:
I. Ao associarmos algumas parcelas o total fica inalterado sendo assim (a + b) + c = a + (b + c) , podemos dizer que essa propriedade se refere a distributiva.
II. A multiplicação em IN pode envolver duas ideias: a de adição de parcelas iguais e o raciocínio combinatório.
III. Pode considerar a operação de multiplicação como uma função que associa a cada par ordenado (a,b) de números naturais, um único número natural c = a.b.
E correto que se afirma em:
II apenas
Apenas I e III
I,II e III
Apenas II e III
Apenas I e II
Em uma tempestade temos trovões, raios e relâmpagos. Lucas era fascinado por esses fenômenos e para impressionar sua paquera marcou no relógio com que frequência cada um desses fenômenos aconteciam, e descobriu que os trovões aconteciam de 5 em 5 minutos, raios de 10 em 10 minutos e por fim os relâmpagos de 3 em 3 minutos. Percebeu também que em um determinado momento os 3 aconteceram simultaneamente. Para impressionar a garota ele deseja mostrar que vai prever quando eles ocorrerão novamente.
Pergunto, em quantos minutos desde que ele notou a primeira ocorrência simultanea acontecerá novamente esses fenômenos ?
A cada 25 minutos
A cada 30 minutos
A cada 15 minutos
A cada 20 minutos
A cada 45 minutos
Observando o número S = 212.57.114, dos números a seguir, qual poderá der divisor de S:
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente
132
131
48
89
101
Duas composições de metrô de Uberinha partem simultaneamente de um mesmo terminal fazendo itinerários diferentes. Uma torna a partir do terminal a cada 80 minutos; a outra a cada hora e meia. Qual é o tempo percorrido entre duas partidas simultâneas consecutivas do termina?
15 horas
10 horas
20 horas
12 horas
15 horas
Pelo algoritmo de Euclides podemos afirmar que o MDC(54,70) é igual ao:
MDC(4,5)
MDC(22,4)
MDC (70,3)
MDC(12,3)
MDC(3,5)
Considere os números A e B, estão transcritos no sistema binário, sendo A = (10101) e B = (11010) , transcrevendo-os para o sistema de numeração de base 10 , o valor de B - A é igual a:
7
6
5
12
10
Dividimos sucessivamente o número da base decimal por 8 até que não seja mais divisível, ao final, o número na base octal é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter 2834 para a base 8.

Ou seja 2834 = 5422 8 .
Seguindo o exposto acima, é correto afirmar que a conversão do número 3564 da base decimal para a base octal é exatamente:
6457 8
6834 8
6750 8
6725 8
6754 8
A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se pode realizar entre eles. Sabe-se que operar implica agir sobre um objeto ou sobre uma situação, realizar transformações e obter um efeito ou um resultado, então leia os itens a seguir:
I. Ao associarmos algumas parcelas o total fica inalterado sendo assim (a + b) + c = a + (b + c) , podemos dizer que essa propriedade se refere a distributiva.
II. A multiplicação em IN pode envolver duas ideias: a de adição de parcelas iguais e o raciocínio combinatório.
III. Pode considerar a operação de multiplicação como uma função que associa a cada par ordenado (a,b) de números naturais, um único número natural c = a.b.
E correto que se afirma em:
II apenas
Apenas I e III
I,II e III
Apenas II e III
Apenas I e II
Em uma tempestade temos trovões, raios e relâmpagos. Lucas era fascinado por esses fenômenos e para impressionar sua paquera marcou no relógio com que frequência cada um desses fenômenos aconteciam, e descobriu que os trovões aconteciam de 5 em 5 minutos, raios de 10 em 10 minutos e por fim os relâmpagos de 3 em 3 minutos. Percebeu também que em um determinado momento os 3 aconteceram simultaneamente. Para impressionar a garota ele deseja mostrar que vai prever quando eles ocorrerão novamente.
Pergunto, em quantos minutos desde que ele notou a primeira ocorrência simultanea acontecerá novamente esses fenômenos ?
A cada 25 minutos
A cada 30 minutos
A cada 15 minutos
A cada 20 minutos
A cada 45 minutos
Observando o número S = 212.57.114, dos números a seguir, qual poderá der divisor de S:
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente
15 horas
10 horas
20 horas
12 horas
15 horas
Pelo algoritmo de Euclides podemos afirmar que o MDC(54,70) é igual ao:
MDC(4,5)
MDC(22,4)
MDC (70,3)
MDC(12,3)
MDC(3,5)
Considere os números A e B, estão transcritos no sistema binário, sendo A = (10101) e B = (11010) , transcrevendo-os para o sistema de numeração de base 10 , o valor de B - A é igual a:
7
6
5
12
10
Dividimos sucessivamente o número da base decimal por 8 até que não seja mais divisível, ao final, o número na base octal é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter 2834 para a base 8.

Ou seja 2834 = 5422 8 .
Seguindo o exposto acima, é correto afirmar que a conversão do número 3564 da base decimal para a base octal é exatamente:
6457 8
6834 8
6750 8
6725 8
6754 8
A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se pode realizar entre eles. Sabe-se que operar implica agir sobre um objeto ou sobre uma situação, realizar transformações e obter um efeito ou um resultado, então leia os itens a seguir:
I. Ao associarmos algumas parcelas o total fica inalterado sendo assim (a + b) + c = a + (b + c) , podemos dizer que essa propriedade se refere a distributiva.
II. A multiplicação em IN pode envolver duas ideias: a de adição de parcelas iguais e o raciocínio combinatório.
III. Pode considerar a operação de multiplicação como uma função que associa a cada par ordenado (a,b) de números naturais, um único número natural c = a.b.
E correto que se afirma em:
II apenas
Apenas I e III
I,II e III
Apenas II e III
Apenas I e II
Em uma tempestade temos trovões, raios e relâmpagos. Lucas era fascinado por esses fenômenos e para impressionar sua paquera marcou no relógio com que frequência cada um desses fenômenos aconteciam, e descobriu que os trovões aconteciam de 5 em 5 minutos, raios de 10 em 10 minutos e por fim os relâmpagos de 3 em 3 minutos. Percebeu também que em um determinado momento os 3 aconteceram simultaneamente. Para impressionar a garota ele deseja mostrar que vai prever quando eles ocorrerão novamente.
Pergunto, em quantos minutos desde que ele notou a primeira ocorrência simultanea acontecerá novamente esses fenômenos ?
A cada 25 minutos
A cada 30 minutos
A cada 15 minutos
A cada 20 minutos
A cada 45 minutos
Observando o número S = 212.57.114, dos números a seguir, qual poderá der divisor de S:
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente
MDC(4,5)
MDC(22,4)
MDC (70,3)
MDC(12,3)
MDC(3,5)
Considere os números A e B, estão transcritos no sistema binário, sendo A = (10101) e B = (11010) , transcrevendo-os para o sistema de numeração de base 10 , o valor de B - A é igual a:
7
6
5
12
10
Dividimos sucessivamente o número da base decimal por 8 até que não seja mais divisível, ao final, o número na base octal é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter 2834 para a base 8.

Ou seja 2834 = 5422 8 .
Seguindo o exposto acima, é correto afirmar que a conversão do número 3564 da base decimal para a base octal é exatamente:
6457 8
6834 8
6750 8
6725 8
6754 8
A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se pode realizar entre eles. Sabe-se que operar implica agir sobre um objeto ou sobre uma situação, realizar transformações e obter um efeito ou um resultado, então leia os itens a seguir:
I. Ao associarmos algumas parcelas o total fica inalterado sendo assim (a + b) + c = a + (b + c) , podemos dizer que essa propriedade se refere a distributiva.
II. A multiplicação em IN pode envolver duas ideias: a de adição de parcelas iguais e o raciocínio combinatório.
III. Pode considerar a operação de multiplicação como uma função que associa a cada par ordenado (a,b) de números naturais, um único número natural c = a.b.
E correto que se afirma em:
II apenas
Apenas I e III
I,II e III
Apenas II e III
Apenas I e II
Em uma tempestade temos trovões, raios e relâmpagos. Lucas era fascinado por esses fenômenos e para impressionar sua paquera marcou no relógio com que frequência cada um desses fenômenos aconteciam, e descobriu que os trovões aconteciam de 5 em 5 minutos, raios de 10 em 10 minutos e por fim os relâmpagos de 3 em 3 minutos. Percebeu também que em um determinado momento os 3 aconteceram simultaneamente. Para impressionar a garota ele deseja mostrar que vai prever quando eles ocorrerão novamente.
Pergunto, em quantos minutos desde que ele notou a primeira ocorrência simultanea acontecerá novamente esses fenômenos ?
A cada 25 minutos
A cada 30 minutos
A cada 15 minutos
A cada 20 minutos
A cada 45 minutos
Observando o número S = 212.57.114, dos números a seguir, qual poderá der divisor de S:
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente
7
6
5
12
10
Dividimos sucessivamente o número da base decimal por 8 até que não seja mais divisível, ao final, o número na base octal é o resultado da última divisão ajuntado dos restos das divisões “de baixo para cima”.
Vamos converter 2834 para a base 8.

Ou seja 2834 = 5422 8 .
Seguindo o exposto acima, é correto afirmar que a conversão do número 3564 da base decimal para a base octal é exatamente:
6457 8
6834 8
6750 8
6725 8
6754 8
A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se pode realizar entre eles. Sabe-se que operar implica agir sobre um objeto ou sobre uma situação, realizar transformações e obter um efeito ou um resultado, então leia os itens a seguir:
I. Ao associarmos algumas parcelas o total fica inalterado sendo assim (a + b) + c = a + (b + c) , podemos dizer que essa propriedade se refere a distributiva.
II. A multiplicação em IN pode envolver duas ideias: a de adição de parcelas iguais e o raciocínio combinatório.
III. Pode considerar a operação de multiplicação como uma função que associa a cada par ordenado (a,b) de números naturais, um único número natural c = a.b.
E correto que se afirma em:
II apenas
Apenas I e III
I,II e III
Apenas II e III
Apenas I e II
Em uma tempestade temos trovões, raios e relâmpagos. Lucas era fascinado por esses fenômenos e para impressionar sua paquera marcou no relógio com que frequência cada um desses fenômenos aconteciam, e descobriu que os trovões aconteciam de 5 em 5 minutos, raios de 10 em 10 minutos e por fim os relâmpagos de 3 em 3 minutos. Percebeu também que em um determinado momento os 3 aconteceram simultaneamente. Para impressionar a garota ele deseja mostrar que vai prever quando eles ocorrerão novamente.
Pergunto, em quantos minutos desde que ele notou a primeira ocorrência simultanea acontecerá novamente esses fenômenos ?
A cada 25 minutos
A cada 30 minutos
A cada 15 minutos
A cada 20 minutos
A cada 45 minutos
Observando o número S = 212.57.114, dos números a seguir, qual poderá der divisor de S:
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente

6457 8
6834 8
6750 8
6725 8
6754 8
A aritmética é a parte da matemática que estuda as propriedades dos números e as operações que se pode realizar entre eles. Sabe-se que operar implica agir sobre um objeto ou sobre uma situação, realizar transformações e obter um efeito ou um resultado, então leia os itens a seguir:
I. Ao associarmos algumas parcelas o total fica inalterado sendo assim (a + b) + c = a + (b + c) , podemos dizer que essa propriedade se refere a distributiva.
II. A multiplicação em IN pode envolver duas ideias: a de adição de parcelas iguais e o raciocínio combinatório.
III. Pode considerar a operação de multiplicação como uma função que associa a cada par ordenado (a,b) de números naturais, um único número natural c = a.b.
E correto que se afirma em:
II apenas
Apenas I e III
I,II e III
Apenas II e III
Apenas I e II
Em uma tempestade temos trovões, raios e relâmpagos. Lucas era fascinado por esses fenômenos e para impressionar sua paquera marcou no relógio com que frequência cada um desses fenômenos aconteciam, e descobriu que os trovões aconteciam de 5 em 5 minutos, raios de 10 em 10 minutos e por fim os relâmpagos de 3 em 3 minutos. Percebeu também que em um determinado momento os 3 aconteceram simultaneamente. Para impressionar a garota ele deseja mostrar que vai prever quando eles ocorrerão novamente.
Pergunto, em quantos minutos desde que ele notou a primeira ocorrência simultanea acontecerá novamente esses fenômenos ?
A cada 25 minutos
A cada 30 minutos
A cada 15 minutos
A cada 20 minutos
A cada 45 minutos
Observando o número S = 212.57.114, dos números a seguir, qual poderá der divisor de S:
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente
II apenas
Apenas I e III
I,II e III
Apenas II e III
Apenas I e II
Em uma tempestade temos trovões, raios e relâmpagos. Lucas era fascinado por esses fenômenos e para impressionar sua paquera marcou no relógio com que frequência cada um desses fenômenos aconteciam, e descobriu que os trovões aconteciam de 5 em 5 minutos, raios de 10 em 10 minutos e por fim os relâmpagos de 3 em 3 minutos. Percebeu também que em um determinado momento os 3 aconteceram simultaneamente. Para impressionar a garota ele deseja mostrar que vai prever quando eles ocorrerão novamente.
Pergunto, em quantos minutos desde que ele notou a primeira ocorrência simultanea acontecerá novamente esses fenômenos ?
A cada 25 minutos
A cada 30 minutos
A cada 15 minutos
A cada 20 minutos
A cada 45 minutos
Observando o número S = 212.57.114, dos números a seguir, qual poderá der divisor de S:
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente
A cada 25 minutos
A cada 30 minutos
A cada 15 minutos
A cada 20 minutos
A cada 45 minutos
Observando o número S = 212.57.114, dos números a seguir, qual poderá der divisor de S:
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente
N = 211.56.115
N = 58.113
N =214.50.113
N = 210.37
N = 210.53.112
De acordo com que estudou no livro de Divisibilidade, podemos salientar que os problemas que envolvem a operação da divisão de números naturais se referem a uma coleção de elementos organizados em uma certa quantidade de grupos, sendo que cada grupo possui a mesma quantidade de elementos. Então podemos verificar que em uma divisão se o divisor é 5 e o resto é 3. Caso multiplicarmos o dividendo e o divisor por 2, podemos corretamente afirmar que o:
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6
Sejam os números A = 33 . 52 . 7 e B = 3 . 53 . 72. O MDC e o MMC entre A e B valem, respectivamente
Resto deverá ser o dobro
Resto fica multiplicado pela metade
Quociente fica multiplicado por 3
Quociente se altera.
Quociente fica multiplicado por 6