TEORIA DAS ESTRUTURAS II

Δ2 = 164,11/EI
Δ2 = 53,74/EI
Δ2 = -167,20/EI
Δ2 = -402,56/EI
Δ2 = 749,04/EI
Calcule a deslocabilidade externa da estrutura abaixo:
– 9
– 3
– 1
– 2
– 7

Δ1 = -459,98/EI
Δ1 = 285,36/EI
Δ1 = -523,48/EI
Δ1 = -321,09/EI
Δ1 = 257,60/EI
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó C, trecho CF

0,339.
0,264.
0,330.
0,397.
0,293.
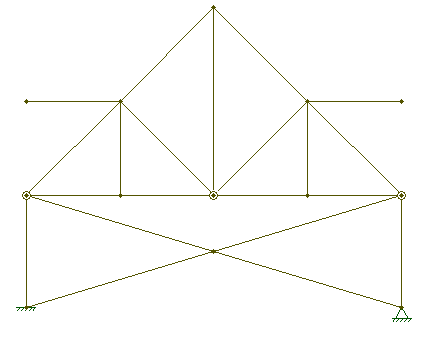
Calcule o grau de deslocabilidade externa (de) da estrutura abaixo. Considere que a corda que está içando o peso não tem rigidez, portanto não participa da análise estrutural.

1
2
-1
3
0
Pelo método dos deslocamentos calcule o momento fletor atuante na estrutura [2] criada referente ao nó "C".
-0,4 EI e -0,67 EI
-0,8 EI e -1,33 EI
0,8 EI e 1,33 EI
EI e -EI
0,4 EI e 0,67 EI

MD = 316,57 kN.m
MD = 392,05 kN.m
MD = 177,58 kN.m
MD = 610,37 kN.m
MD = 32,46 kN.m
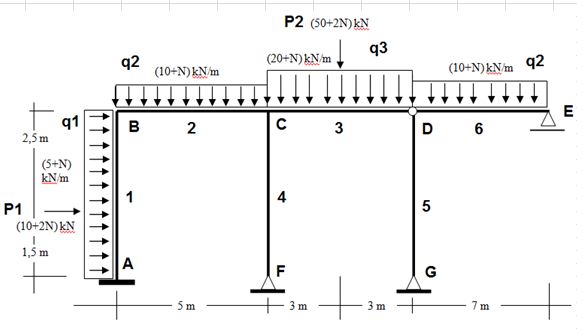
Determine, através do Método dos Deslocamentos, o momento Mc3 do pórtico abaixo, considerando N = 2:
153,3
146,25
180,1
121,1
207,4
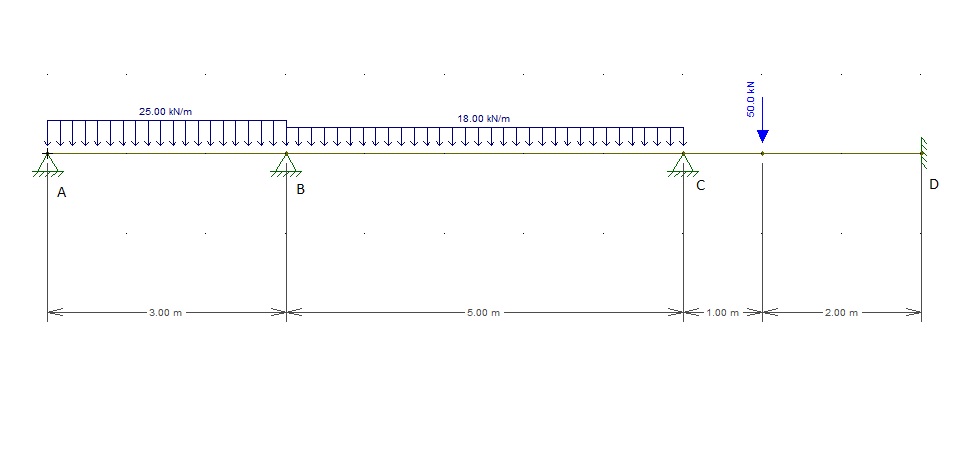
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Δ2 = 164,11/EI
Δ2 = 53,74/EI
Δ2 = -167,20/EI
Δ2 = -402,56/EI
Δ2 = 749,04/EI
Calcule a deslocabilidade externa da estrutura abaixo:

– 9
– 3
– 1
– 2
– 7

Δ1 = -459,98/EI
Δ1 = 285,36/EI
Δ1 = -523,48/EI
Δ1 = -321,09/EI
Δ1 = 257,60/EI
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó C, trecho CF

0,339.
0,264.
0,330.
0,397.
0,293.
Calcule o grau de deslocabilidade externa (de) da estrutura abaixo. Considere que a corda que está içando o peso não tem rigidez, portanto não participa da análise estrutural.

1
2
-1
3
0
Pelo método dos deslocamentos calcule o momento fletor atuante na estrutura [2] criada referente ao nó "C".

-0,4 EI e -0,67 EI
-0,8 EI e -1,33 EI
0,8 EI e 1,33 EI
EI e -EI
0,4 EI e 0,67 EI

MD = 316,57 kN.m
MD = 392,05 kN.m
MD = 177,58 kN.m
MD = 610,37 kN.m
MD = 32,46 kN.m
Determine, através do Método dos Deslocamentos, o momento Mc3 do pórtico abaixo, considerando N = 2:

153,3
146,25
180,1
121,1
207,4
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.

– 9
– 3
– 1
– 2
– 7

Δ1 = -459,98/EI
Δ1 = 285,36/EI
Δ1 = -523,48/EI
Δ1 = -321,09/EI
Δ1 = 257,60/EI
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó C, trecho CF

0,339.
0,264.
0,330.
0,397.
0,293.
Calcule o grau de deslocabilidade externa (de) da estrutura abaixo. Considere que a corda que está içando o peso não tem rigidez, portanto não participa da análise estrutural.

1
2
-1
3
0
Pelo método dos deslocamentos calcule o momento fletor atuante na estrutura [2] criada referente ao nó "C".

-0,4 EI e -0,67 EI
-0,8 EI e -1,33 EI
0,8 EI e 1,33 EI
EI e -EI
0,4 EI e 0,67 EI

MD = 316,57 kN.m
MD = 392,05 kN.m
MD = 177,58 kN.m
MD = 610,37 kN.m
MD = 32,46 kN.m
Determine, através do Método dos Deslocamentos, o momento Mc3 do pórtico abaixo, considerando N = 2:

153,3
146,25
180,1
121,1
207,4
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Δ1 = -459,98/EI
Δ1 = 285,36/EI
Δ1 = -523,48/EI
Δ1 = -321,09/EI
Δ1 = 257,60/EI
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó C, trecho CF

0,339.
0,264.
0,330.
0,397.
0,293.
Calcule o grau de deslocabilidade externa (de) da estrutura abaixo. Considere que a corda que está içando o peso não tem rigidez, portanto não participa da análise estrutural.

1
2
-1
3
0
Pelo método dos deslocamentos calcule o momento fletor atuante na estrutura [2] criada referente ao nó "C".

-0,4 EI e -0,67 EI
-0,8 EI e -1,33 EI
0,8 EI e 1,33 EI
EI e -EI
0,4 EI e 0,67 EI

MD = 316,57 kN.m
MD = 392,05 kN.m
MD = 177,58 kN.m
MD = 610,37 kN.m
MD = 32,46 kN.m
Determine, através do Método dos Deslocamentos, o momento Mc3 do pórtico abaixo, considerando N = 2:

153,3
146,25
180,1
121,1
207,4
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
0,339.
0,264.
0,330.
0,397.
0,293.
Calcule o grau de deslocabilidade externa (de) da estrutura abaixo. Considere que a corda que está içando o peso não tem rigidez, portanto não participa da análise estrutural.

1
2
-1
3
0
Pelo método dos deslocamentos calcule o momento fletor atuante na estrutura [2] criada referente ao nó "C".

-0,4 EI e -0,67 EI
-0,8 EI e -1,33 EI
0,8 EI e 1,33 EI
EI e -EI
0,4 EI e 0,67 EI

MD = 316,57 kN.m
MD = 392,05 kN.m
MD = 177,58 kN.m
MD = 610,37 kN.m
MD = 32,46 kN.m
Determine, através do Método dos Deslocamentos, o momento Mc3 do pórtico abaixo, considerando N = 2:

153,3
146,25
180,1
121,1
207,4
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
1
2
-1
3
0
Pelo método dos deslocamentos calcule o momento fletor atuante na estrutura [2] criada referente ao nó "C".

-0,4 EI e -0,67 EI
-0,8 EI e -1,33 EI
0,8 EI e 1,33 EI
EI e -EI
0,4 EI e 0,67 EI

MD = 316,57 kN.m
MD = 392,05 kN.m
MD = 177,58 kN.m
MD = 610,37 kN.m
MD = 32,46 kN.m
Determine, através do Método dos Deslocamentos, o momento Mc3 do pórtico abaixo, considerando N = 2:

153,3
146,25
180,1
121,1
207,4
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.

-0,4 EI e -0,67 EI
-0,8 EI e -1,33 EI
0,8 EI e 1,33 EI
EI e -EI
0,4 EI e 0,67 EI

MD = 316,57 kN.m
MD = 392,05 kN.m
MD = 177,58 kN.m
MD = 610,37 kN.m
MD = 32,46 kN.m
Determine, através do Método dos Deslocamentos, o momento Mc3 do pórtico abaixo, considerando N = 2:

153,3
146,25
180,1
121,1
207,4
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
MD = 316,57 kN.m
MD = 392,05 kN.m
MD = 177,58 kN.m
MD = 610,37 kN.m
MD = 32,46 kN.m
Determine, através do Método dos Deslocamentos, o momento Mc3 do pórtico abaixo, considerando N = 2:

153,3
146,25
180,1
121,1
207,4
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.

153,3
146,25
180,1
121,1
207,4
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:
obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Considere também que esta estrutura tem inércia variável da seguinte forma: Trecho AB = 3 EI ; Trecho BC = 4 EI ; Trecho CD = 2EI ; Trecho BE = EI ;Trecho CF = EI.

Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI
Encontre o valor de Δ1 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo:

obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação.
Δ1 = -52,048/EI
Δ1 = -37,365/EI
Δ1 = -74,315/EI
Δ1 = -63,542/EI
Δ1 = -45,122/EI