TEORIA DAS ESTRUTURAS II

Δ2 = 53,74/EI
Δ2 = 749,04/EI
Δ2 = -402,56/EI
Δ2 = 164,11/EI
Δ2 = -167,20/EI
As figuras 1,2 e 3, a seguir, apresentam,respectivamente, o esquema estático de uma viga contínua (com EI constante) e seus diagramas de momento fletor e de esforço cortante.

Com base nas figuras e considerando que Q1 e Q2 são cargas uniformemente distribuídas; P1,P2 e P3 são cargas concentradas.
avalie as afirmações a seguir:
- A carga pontual P2 tem valor de 40,0 kN.
- A carga uniformemente distribuída Q2 tem valor de 60,0 kN/m.
- A reação vertical n o apoio F tem valor de 184,4 kN.
É correto o qe se afirma em:
I,II e III.
I e II, apenas.
I,apenas.
III,apenas
II e III, apenas.
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 3;Barra BC, EI2 = 6;barra CD, EI3= 4.
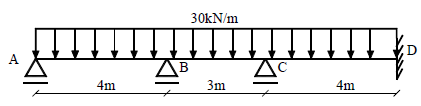
MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 49,1 kN.m; MD =46,6kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;

MA = 392,05 kN.m
MA = 32,46 kN.m
MA = 177,58 kN.m
MA = 316,57 kN.m
MA = -388,19 kN.m

Δ1 = -92,70/EI
Δ1 = -428,02/EI
Δ1 = -73,85/EI
Δ1 = -124,44/EI
Δ1 = -396,27/EI

MBesq. = 392,05 kN.m
MBesq. = 32,46 kN.m
MBesq. = 316,57 kN.m
MBesq. = 177,58 kN.m
MBesq. = -388,19 kN.m
Encontre o valor de Δ2 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia constante da seguinte forma: Trecho AB = EI ; Trecho BC = EI ; Trecho CD = EI ; Trecho BE = EI ;Trecho CF = EI.

-298,990/EI
158,551/EI
160,209/EI
-80,246/EI
-139,344/EI
Assinale a alternativa correta que apresenta o valor da deslocabilidade interna “di” da viga ilustrada a seguir.

Δ2 = 53,74/EI
Δ2 = 749,04/EI
Δ2 = -402,56/EI
Δ2 = 164,11/EI
Δ2 = -167,20/EI
As figuras 1,2 e 3, a seguir, apresentam,respectivamente, o esquema estático de uma viga contínua (com EI constante) e seus diagramas de momento fletor e de esforço cortante.

Com base nas figuras e considerando que Q1 e Q2 são cargas uniformemente distribuídas; P1,P2 e P3 são cargas concentradas.
avalie as afirmações a seguir:
- A carga pontual P2 tem valor de 40,0 kN.
- A carga uniformemente distribuída Q2 tem valor de 60,0 kN/m.
- A reação vertical n o apoio F tem valor de 184,4 kN.
É correto o qe se afirma em:
I,II e III.
I e II, apenas.
I,apenas.
III,apenas
II e III, apenas.
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 3;Barra BC, EI2 = 6;barra CD, EI3= 4.

MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 49,1 kN.m; MD =46,6kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;

MA = 392,05 kN.m
MA = 32,46 kN.m
MA = 177,58 kN.m
MA = 316,57 kN.m
MA = -388,19 kN.m

Δ1 = -92,70/EI
Δ1 = -428,02/EI
Δ1 = -73,85/EI
Δ1 = -124,44/EI
Δ1 = -396,27/EI

MBesq. = 392,05 kN.m
MBesq. = 32,46 kN.m
MBesq. = 316,57 kN.m
MBesq. = 177,58 kN.m
MBesq. = -388,19 kN.m
Encontre o valor de Δ2 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia constante da seguinte forma: Trecho AB = EI ; Trecho BC = EI ; Trecho CD = EI ; Trecho BE = EI ;Trecho CF = EI.

-298,990/EI
158,551/EI
160,209/EI
-80,246/EI
-139,344/EI
Assinale a alternativa correta que apresenta o valor da deslocabilidade interna “di” da viga ilustrada a seguir.

I,II e III.
I e II, apenas.
I,apenas.
III,apenas
II e III, apenas.
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 3;Barra BC, EI2 = 6;barra CD, EI3= 4.

MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 49,1 kN.m; MD =46,6kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;

MA = 392,05 kN.m
MA = 32,46 kN.m
MA = 177,58 kN.m
MA = 316,57 kN.m
MA = -388,19 kN.m

Δ1 = -92,70/EI
Δ1 = -428,02/EI
Δ1 = -73,85/EI
Δ1 = -124,44/EI
Δ1 = -396,27/EI

MBesq. = 392,05 kN.m
MBesq. = 32,46 kN.m
MBesq. = 316,57 kN.m
MBesq. = 177,58 kN.m
MBesq. = -388,19 kN.m
Encontre o valor de Δ2 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia constante da seguinte forma: Trecho AB = EI ; Trecho BC = EI ; Trecho CD = EI ; Trecho BE = EI ;Trecho CF = EI.

-298,990/EI
158,551/EI
160,209/EI
-80,246/EI
-139,344/EI
Assinale a alternativa correta que apresenta o valor da deslocabilidade interna “di” da viga ilustrada a seguir.


MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 49,1 kN.m; MD =46,6kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;

MA = 392,05 kN.m
MA = 32,46 kN.m
MA = 177,58 kN.m
MA = 316,57 kN.m
MA = -388,19 kN.m

Δ1 = -92,70/EI
Δ1 = -428,02/EI
Δ1 = -73,85/EI
Δ1 = -124,44/EI
Δ1 = -396,27/EI

MBesq. = 392,05 kN.m
MBesq. = 32,46 kN.m
MBesq. = 316,57 kN.m
MBesq. = 177,58 kN.m
MBesq. = -388,19 kN.m
Encontre o valor de Δ2 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia constante da seguinte forma: Trecho AB = EI ; Trecho BC = EI ; Trecho CD = EI ; Trecho BE = EI ;Trecho CF = EI.

-298,990/EI
158,551/EI
160,209/EI
-80,246/EI
-139,344/EI
Assinale a alternativa correta que apresenta o valor da deslocabilidade interna “di” da viga ilustrada a seguir.

MA = 392,05 kN.m
MA = 32,46 kN.m
MA = 177,58 kN.m
MA = 316,57 kN.m
MA = -388,19 kN.m

Δ1 = -92,70/EI
Δ1 = -428,02/EI
Δ1 = -73,85/EI
Δ1 = -124,44/EI
Δ1 = -396,27/EI

MBesq. = 392,05 kN.m
MBesq. = 32,46 kN.m
MBesq. = 316,57 kN.m
MBesq. = 177,58 kN.m
MBesq. = -388,19 kN.m
Encontre o valor de Δ2 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia constante da seguinte forma: Trecho AB = EI ; Trecho BC = EI ; Trecho CD = EI ; Trecho BE = EI ;Trecho CF = EI.

-298,990/EI
158,551/EI
160,209/EI
-80,246/EI
-139,344/EI
Assinale a alternativa correta que apresenta o valor da deslocabilidade interna “di” da viga ilustrada a seguir.

Δ1 = -92,70/EI
Δ1 = -428,02/EI
Δ1 = -73,85/EI
Δ1 = -124,44/EI
Δ1 = -396,27/EI

MBesq. = 392,05 kN.m
MBesq. = 32,46 kN.m
MBesq. = 316,57 kN.m
MBesq. = 177,58 kN.m
MBesq. = -388,19 kN.m
Encontre o valor de Δ2 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia constante da seguinte forma: Trecho AB = EI ; Trecho BC = EI ; Trecho CD = EI ; Trecho BE = EI ;Trecho CF = EI.

-298,990/EI
158,551/EI
160,209/EI
-80,246/EI
-139,344/EI
Assinale a alternativa correta que apresenta o valor da deslocabilidade interna “di” da viga ilustrada a seguir.

MBesq. = 392,05 kN.m
MBesq. = 32,46 kN.m
MBesq. = 316,57 kN.m
MBesq. = 177,58 kN.m
MBesq. = -388,19 kN.m
Encontre o valor de Δ2 da equação geral : M [r] = M [0] + Δ1 x M [1] + Δ2 x M [2] + ... + Δi x M [i] , utilizando o método dos deslocamentos para a estrutura representada na figura abaixo: obs: para fazer os cálculos com a calculadora deve ser utilizado todas as casas sem aproximação. Considere também que esta estrutura tem inércia constante da seguinte forma: Trecho AB = EI ; Trecho BC = EI ; Trecho CD = EI ; Trecho BE = EI ;Trecho CF = EI.

-298,990/EI
158,551/EI
160,209/EI
-80,246/EI
-139,344/EI
Assinale a alternativa correta que apresenta o valor da deslocabilidade interna “di” da viga ilustrada a seguir.

-298,990/EI
158,551/EI
160,209/EI
-80,246/EI
-139,344/EI
Assinale a alternativa correta que apresenta o valor da deslocabilidade interna “di” da viga ilustrada a seguir.

