TEORIA DAS ESTRUTURAS II
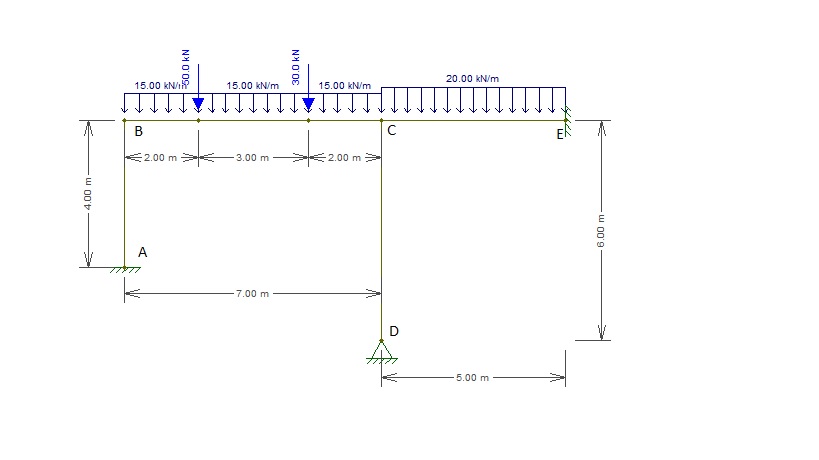
Qual o valor do momento fletor no ponto "E" do pórtico abaixo. Utilize o processo de CROSS para resolução.
-44,0 KN.m
-88,6 KN.m
-12,2 KN.m
-21,2 KN.m
-69,5 KN.m
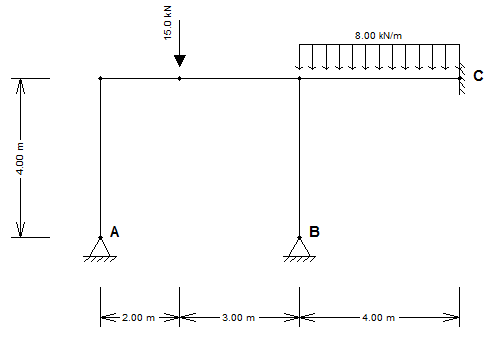
Analise o pórtico representado na figura abaixo. Em seguida, assinale a alternativa CORRETA que apresenta os valores da reação de apoio no ponto A, considerando o produto E.I constante.
RvA = 8,00 kN e RHA = 1,29 kN
RvA = 10,00 kN e RHA = 2,49 kN
RvA = 10,00 kN e RHA = 1,29 kN
RvA = 10,00 kN e RHA = -1,29 kN
RvA = 8,00 kN e RHA = 2,49 kN
"Sabe-se que o coeficiente de distribuição de momento de uma barra com relação a um nó é a razão entre o coeficiente de rigidez à rotação da barra e o somatório dos coeficientes de rigidez à rotação de todas as barras que convergem no nó".
Com base na informação anterior assinale a alternativa CORRETA que apresenta o valor do somatório de todos os coeficientes de distribuição de momento de todas as barras adjacentes a um determinado nó.
2
3
1
100
0,50
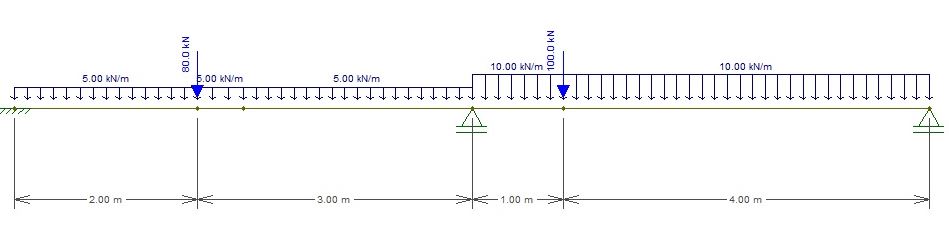
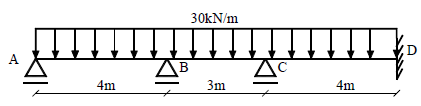
Calcule o valor do momento atuante sobre o apoio central utilizando o método dos deslocamentos.
- 125,5 KN.m
- 98,6 KN.m
- 79,9 KN.m
- 6,35 Kn.m
- 32,5 KN.m
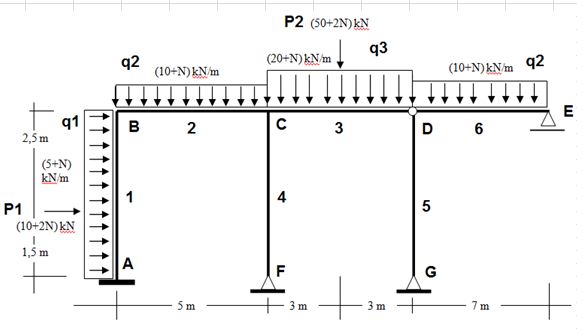
Determine, através do Método dos Deslocamentos, o momento Mc2 do pórtico abaixo, considerando N =11:
-152,60
147,92
-125
151
141,67
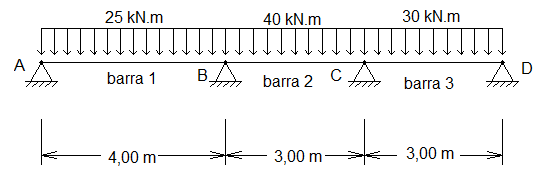
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 5;Barra BC, EI2 = 3;barra CD, EI3= 8.
MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;
MA = 0 Kn.m; MB =39,6 kN.m; MC = 21,1 kN.m; MD =49,5kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
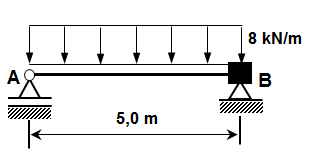
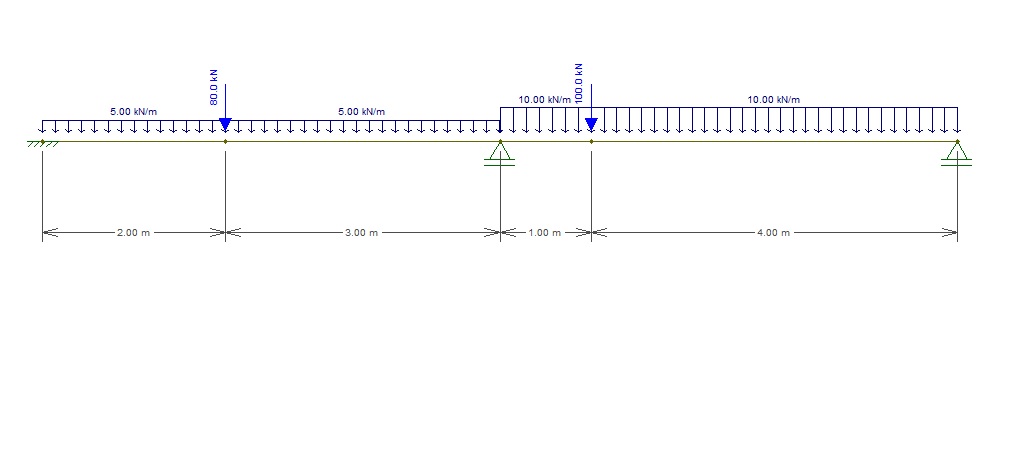
Com base na viga ilustrada a seguir, marque a alternativa que apresenta o valor correto da reação de apoio vertical no ponto C. Para tanto, utilize o método das deformações e considere o produto E.I = constante.
98,23 kN
67,23 kN
110,43 kN
124,63 kN
79,22 kN
Utilizando o método dos deslocamentos calcule o valor do cortante no meio do trecho AB, considerando o primeiro apoio como A o segundo B e o terceiro D, faça o desenvolvimento das equações, demonstrando como chegou nos resultados, sabe-se que EI é constante.

-44,0 KN.m
-88,6 KN.m
-12,2 KN.m
-21,2 KN.m
-69,5 KN.m
Analise o pórtico representado na figura abaixo. Em seguida, assinale a alternativa CORRETA que apresenta os valores da reação de apoio no ponto A, considerando o produto E.I constante.

RvA = 8,00 kN e RHA = 1,29 kN
RvA = 10,00 kN e RHA = 2,49 kN
RvA = 10,00 kN e RHA = 1,29 kN
RvA = 10,00 kN e RHA = -1,29 kN
RvA = 8,00 kN e RHA = 2,49 kN
"Sabe-se que o coeficiente de distribuição de momento de uma barra com relação a um nó é a razão entre o coeficiente de rigidez à rotação da barra e o somatório dos coeficientes de rigidez à rotação de todas as barras que convergem no nó".
Com base na informação anterior assinale a alternativa CORRETA que apresenta o valor do somatório de todos os coeficientes de distribuição de momento de todas as barras adjacentes a um determinado nó.
2
3
1
100
0,50
Calcule o valor do momento atuante sobre o apoio central utilizando o método dos deslocamentos.

- 125,5 KN.m
- 98,6 KN.m
- 79,9 KN.m
- 6,35 Kn.m
- 32,5 KN.m
Determine, através do Método dos Deslocamentos, o momento Mc2 do pórtico abaixo, considerando N =11:

-152,60
147,92
-125
151
141,67
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 5;Barra BC, EI2 = 3;barra CD, EI3= 8.

MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;
MA = 0 Kn.m; MB =39,6 kN.m; MC = 21,1 kN.m; MD =49,5kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
Com base na viga ilustrada a seguir, marque a alternativa que apresenta o valor correto da reação de apoio vertical no ponto C. Para tanto, utilize o método das deformações e considere o produto E.I = constante.

98,23 kN
67,23 kN
110,43 kN
124,63 kN
79,22 kN
Utilizando o método dos deslocamentos calcule o valor do cortante no meio do trecho AB, considerando o primeiro apoio como A o segundo B e o terceiro D, faça o desenvolvimento das equações, demonstrando como chegou nos resultados, sabe-se que EI é constante.


RvA = 8,00 kN e RHA = 1,29 kN
RvA = 10,00 kN e RHA = 2,49 kN
RvA = 10,00 kN e RHA = 1,29 kN
RvA = 10,00 kN e RHA = -1,29 kN
RvA = 8,00 kN e RHA = 2,49 kN
"Sabe-se que o coeficiente de distribuição de momento de uma barra com relação a um nó é a razão entre o coeficiente de rigidez à rotação da barra e o somatório dos coeficientes de rigidez à rotação de todas as barras que convergem no nó".
Com base na informação anterior assinale a alternativa CORRETA que apresenta o valor do somatório de todos os coeficientes de distribuição de momento de todas as barras adjacentes a um determinado nó.
2
3
1
100
0,50
Calcule o valor do momento atuante sobre o apoio central utilizando o método dos deslocamentos.

- 125,5 KN.m
- 98,6 KN.m
- 79,9 KN.m
- 6,35 Kn.m
- 32,5 KN.m
Determine, através do Método dos Deslocamentos, o momento Mc2 do pórtico abaixo, considerando N =11:

-152,60
147,92
-125
151
141,67
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 5;Barra BC, EI2 = 3;barra CD, EI3= 8.

MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;
MA = 0 Kn.m; MB =39,6 kN.m; MC = 21,1 kN.m; MD =49,5kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
Com base na viga ilustrada a seguir, marque a alternativa que apresenta o valor correto da reação de apoio vertical no ponto C. Para tanto, utilize o método das deformações e considere o produto E.I = constante.

98,23 kN
67,23 kN
110,43 kN
124,63 kN
79,22 kN
Utilizando o método dos deslocamentos calcule o valor do cortante no meio do trecho AB, considerando o primeiro apoio como A o segundo B e o terceiro D, faça o desenvolvimento das equações, demonstrando como chegou nos resultados, sabe-se que EI é constante.

2
3
1
100
0,50
Calcule o valor do momento atuante sobre o apoio central utilizando o método dos deslocamentos.

- 125,5 KN.m
- 98,6 KN.m
- 79,9 KN.m
- 6,35 Kn.m
- 32,5 KN.m
Determine, através do Método dos Deslocamentos, o momento Mc2 do pórtico abaixo, considerando N =11:

-152,60
147,92
-125
151
141,67
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 5;Barra BC, EI2 = 3;barra CD, EI3= 8.

MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;
MA = 0 Kn.m; MB =39,6 kN.m; MC = 21,1 kN.m; MD =49,5kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
Com base na viga ilustrada a seguir, marque a alternativa que apresenta o valor correto da reação de apoio vertical no ponto C. Para tanto, utilize o método das deformações e considere o produto E.I = constante.

98,23 kN
67,23 kN
110,43 kN
124,63 kN
79,22 kN
Utilizando o método dos deslocamentos calcule o valor do cortante no meio do trecho AB, considerando o primeiro apoio como A o segundo B e o terceiro D, faça o desenvolvimento das equações, demonstrando como chegou nos resultados, sabe-se que EI é constante.


- 125,5 KN.m
- 98,6 KN.m
- 79,9 KN.m
- 6,35 Kn.m
Determine, através do Método dos Deslocamentos, o momento Mc2 do pórtico abaixo, considerando N =11:

-152,60
147,92
-125
151
141,67
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 5;Barra BC, EI2 = 3;barra CD, EI3= 8.

MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;
MA = 0 Kn.m; MB =39,6 kN.m; MC = 21,1 kN.m; MD =49,5kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
Com base na viga ilustrada a seguir, marque a alternativa que apresenta o valor correto da reação de apoio vertical no ponto C. Para tanto, utilize o método das deformações e considere o produto E.I = constante.

98,23 kN
67,23 kN
110,43 kN
124,63 kN
79,22 kN
Utilizando o método dos deslocamentos calcule o valor do cortante no meio do trecho AB, considerando o primeiro apoio como A o segundo B e o terceiro D, faça o desenvolvimento das equações, demonstrando como chegou nos resultados, sabe-se que EI é constante.


-152,60
147,92
-125
151
141,67
Calcule os momentos fletores da estrutura representada na figura abaixo, sabendo que :barra AB ,EI1 = 5;Barra BC, EI2 = 3;barra CD, EI3= 8.

MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;
MA = 0 Kn.m; MB =39,6 kN.m; MC = 21,1 kN.m; MD =49,5kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
Com base na viga ilustrada a seguir, marque a alternativa que apresenta o valor correto da reação de apoio vertical no ponto C. Para tanto, utilize o método das deformações e considere o produto E.I = constante.

98,23 kN
67,23 kN
110,43 kN
124,63 kN
79,22 kN
Utilizando o método dos deslocamentos calcule o valor do cortante no meio do trecho AB, considerando o primeiro apoio como A o segundo B e o terceiro D, faça o desenvolvimento das equações, demonstrando como chegou nos resultados, sabe-se que EI é constante.


MA = 0 Kn.m; MB =46,6 kN.m; MC = 28,2 kN.m; MD =45,9kN.m;
MA = 0 Kn.m; MB =28,2 kN.m; MC = 45,9 kN.m; MD =46,6kN.m;
MA = 0 Kn.m; MB =39,6 kN.m; MC = 21,1 kN.m; MD =49,5kN.m.
MA = 0 Kn.m; MB =49,1 kN.m; MC = 27,7 kN.m; MD =46,2kN.m;
MA = 0 Kn.m; MB =46,6 kN.m; MC = 45,9 kN.m; MD =28,2kN.m;
Com base na viga ilustrada a seguir, marque a alternativa que apresenta o valor correto da reação de apoio vertical no ponto C. Para tanto, utilize o método das deformações e considere o produto E.I = constante.

98,23 kN
67,23 kN
110,43 kN
124,63 kN
79,22 kN
Utilizando o método dos deslocamentos calcule o valor do cortante no meio do trecho AB, considerando o primeiro apoio como A o segundo B e o terceiro D, faça o desenvolvimento das equações, demonstrando como chegou nos resultados, sabe-se que EI é constante.


98,23 kN
67,23 kN
110,43 kN
124,63 kN
79,22 kN
Utilizando o método dos deslocamentos calcule o valor do cortante no meio do trecho AB, considerando o primeiro apoio como A o segundo B e o terceiro D, faça o desenvolvimento das equações, demonstrando como chegou nos resultados, sabe-se que EI é constante.