TEORIA DAS ESTRUTURAS II
Determine o valor do grau de estaticidade da estrutura abaixo. Considere que a ligação em "B" seja uma rótula apenas para barra BC e que para barra AD a ligação seja rígida. O mesmo ocorre na ligação "C" . Após o cálculo, marque a alternativa que apresenta o grau correto e seu significado.
-1; Hipostática
0; Isostática
-2; Hipostática
1; Hipostática
1; Hiperestática
Com base na viga a seguir, calcule as reações de apoio da estrutura abaixo, utilize o Método de Cross para fazer os cálculos.
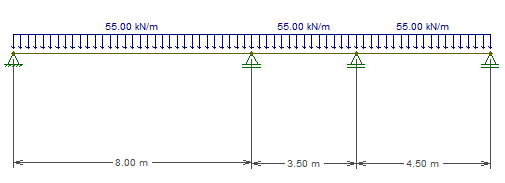
Va = 179,37 ; Vb = 437,14 ; Vc = 149,53 ; Vd =113,95
Va = 139,77 ; Vb = 573,41 ; Vc = 198,35 ; Vd =218,55
Va = 139,77 ; Vb = 337,41 ; Vc = 198,35 ; Vd =218,55
Va = 199,73 ; Vb = 473,41 ; Vc = 107,35 ; Vd =418,55
Va = 199,73 ; Vb = 734,41 ; Vc = 107,35 ; Vd =113,55
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor no nó D - MDE, em módulo.
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
39,39 KN.m
26,26 KN.m
18,18 KN.m
46,46 KN.m
52,52 KN.m
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor no ponto C.
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
8,74 KN.m
35,74 KN.m
19,74 KN.m
28,96 KN.m
1,29 KN.m
Qual o valor do momento fletor no ponto "A" do pórtico abaixo. Utilize o processo de CROSS para resolução.
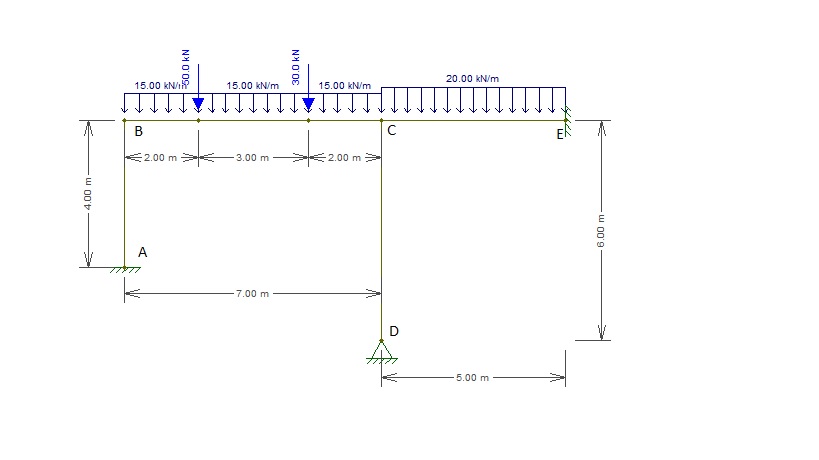
28,5 KN.m
69,5 KN.m
44,3 KN.m
12,3 KN.m
82,6 KN.m
Analise o pórtico representado na figura abaixo. Em seguida, assinale a alternativa CORRETA que apresenta os valores da reação de apoio no ponto B. Considere o produto E.I constante.
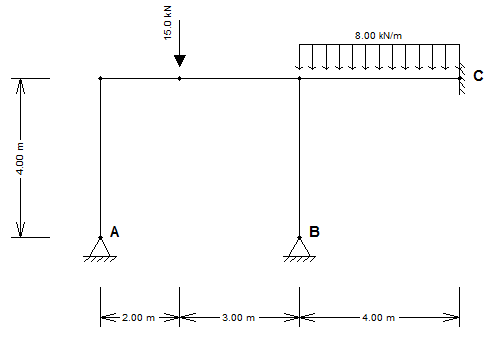
RvB = 22,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = 0,05 kN
RvB = 22,90 kN e RHB = -0,15 kN
RvB =12,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = -0,15 kN
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó B, trecho BE
0,208.
0,241.
0,276.
0,238.
0,483.
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor negativo no nó B - MBD (em módulo).
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.
-1; Hipostática
0; Isostática
-2; Hipostática
1; Hipostática
1; Hiperestática
Com base na viga a seguir, calcule as reações de apoio da estrutura abaixo, utilize o Método de Cross para fazer os cálculos.
Va = 179,37 ; Vb = 437,14 ; Vc = 149,53 ; Vd =113,95
Va = 139,77 ; Vb = 573,41 ; Vc = 198,35 ; Vd =218,55
Va = 139,77 ; Vb = 337,41 ; Vc = 198,35 ; Vd =218,55
Va = 199,73 ; Vb = 473,41 ; Vc = 107,35 ; Vd =418,55
Va = 199,73 ; Vb = 734,41 ; Vc = 107,35 ; Vd =113,55
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor no nó D - MDE, em módulo.
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
39,39 KN.m
26,26 KN.m
18,18 KN.m
46,46 KN.m
52,52 KN.m
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor no ponto C.
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
8,74 KN.m
35,74 KN.m
19,74 KN.m
28,96 KN.m
1,29 KN.m
Qual o valor do momento fletor no ponto "A" do pórtico abaixo. Utilize o processo de CROSS para resolução.
28,5 KN.m
69,5 KN.m
44,3 KN.m
12,3 KN.m
82,6 KN.m
Analise o pórtico representado na figura abaixo. Em seguida, assinale a alternativa CORRETA que apresenta os valores da reação de apoio no ponto B. Considere o produto E.I constante.
RvB = 22,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = 0,05 kN
RvB = 22,90 kN e RHB = -0,15 kN
RvB =12,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = -0,15 kN
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó B, trecho BE
0,208.
0,241.
0,276.
0,238.
0,483.
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor negativo no nó B - MBD (em módulo).
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.
Va = 179,37 ; Vb = 437,14 ; Vc = 149,53 ; Vd =113,95
Va = 139,77 ; Vb = 573,41 ; Vc = 198,35 ; Vd =218,55
Va = 139,77 ; Vb = 337,41 ; Vc = 198,35 ; Vd =218,55
Va = 199,73 ; Vb = 473,41 ; Vc = 107,35 ; Vd =418,55
Va = 199,73 ; Vb = 734,41 ; Vc = 107,35 ; Vd =113,55
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor no nó D - MDE, em módulo.
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
39,39 KN.m
26,26 KN.m
18,18 KN.m
46,46 KN.m
52,52 KN.m
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor no ponto C.
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
8,74 KN.m
35,74 KN.m
19,74 KN.m
28,96 KN.m
1,29 KN.m
Qual o valor do momento fletor no ponto "A" do pórtico abaixo. Utilize o processo de CROSS para resolução.
28,5 KN.m
69,5 KN.m
44,3 KN.m
12,3 KN.m
82,6 KN.m
Analise o pórtico representado na figura abaixo. Em seguida, assinale a alternativa CORRETA que apresenta os valores da reação de apoio no ponto B. Considere o produto E.I constante.
RvB = 22,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = 0,05 kN
RvB = 22,90 kN e RHB = -0,15 kN
RvB =12,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = -0,15 kN
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó B, trecho BE
0,208.
0,241.
0,276.
0,238.
0,483.
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor negativo no nó B - MBD (em módulo).
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.
39,39 KN.m
26,26 KN.m
18,18 KN.m
46,46 KN.m
52,52 KN.m
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor no ponto C.
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
8,74 KN.m
35,74 KN.m
19,74 KN.m
28,96 KN.m
1,29 KN.m
Qual o valor do momento fletor no ponto "A" do pórtico abaixo. Utilize o processo de CROSS para resolução.
28,5 KN.m
69,5 KN.m
44,3 KN.m
12,3 KN.m
82,6 KN.m
Analise o pórtico representado na figura abaixo. Em seguida, assinale a alternativa CORRETA que apresenta os valores da reação de apoio no ponto B. Considere o produto E.I constante.
RvB = 22,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = 0,05 kN
RvB = 22,90 kN e RHB = -0,15 kN
RvB =12,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = -0,15 kN
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó B, trecho BE
0,208.
0,241.
0,276.
0,238.
0,483.
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor negativo no nó B - MBD (em módulo).
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.
8,74 KN.m
35,74 KN.m
19,74 KN.m
28,96 KN.m
1,29 KN.m
Qual o valor do momento fletor no ponto "A" do pórtico abaixo. Utilize o processo de CROSS para resolução.
28,5 KN.m
69,5 KN.m
44,3 KN.m
12,3 KN.m
82,6 KN.m
Analise o pórtico representado na figura abaixo. Em seguida, assinale a alternativa CORRETA que apresenta os valores da reação de apoio no ponto B. Considere o produto E.I constante.
RvB = 22,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = 0,05 kN
RvB = 22,90 kN e RHB = -0,15 kN
RvB =12,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = -0,15 kN
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó B, trecho BE
0,208.
0,241.
0,276.
0,238.
0,483.
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor negativo no nó B - MBD (em módulo).
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.
28,5 KN.m
69,5 KN.m
44,3 KN.m
12,3 KN.m
82,6 KN.m
Analise o pórtico representado na figura abaixo. Em seguida, assinale a alternativa CORRETA que apresenta os valores da reação de apoio no ponto B. Considere o produto E.I constante.
RvB = 22,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = 0,05 kN
RvB = 22,90 kN e RHB = -0,15 kN
RvB =12,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = -0,15 kN
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó B, trecho BE
0,208.
0,241.
0,276.
0,238.
0,483.
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor negativo no nó B - MBD (em módulo).
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.
RvB = 22,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = 0,05 kN
RvB = 22,90 kN e RHB = -0,15 kN
RvB =12,90 kN e RHB = 0,05 kN
RvB =15,90 kN e RHB = -0,15 kN
Utilizando o processo de Cross, determine o coeficiente de distribuição do Nó B, trecho BE
0,208.
0,241.
0,276.
0,238.
0,483.
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor negativo no nó B - MBD (em módulo).
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.
0,208.
0,241.
0,276.
0,238.
0,483.
Baseado no pórtico apresentado abaixo, sabendo-se que as barras AB e DE possuem rigidez de 1 EI e as barras BC e CD, 2 EI, determine o valor do momento fletor negativo no nó B - MBD (em módulo).
Dados para complementar a imagem: Carga triangular: 5 KN/m; Carga uniformente distribuída: 15 KN/m; Carga pontual: 60 KN.
Comprimento dos trechos: AB = 4 m; BC = 4m; CD = 6 m e DE = 4 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.
52,52 KN.m
48,74 KN.m
31,59 KN.m
74,95 KN.m
23,96 KN.m
Baseado na viga contínua apresentada abaixo, sabendo-se que todas as barras possuem a mesma rigidez de 1 EI, determine o valor do momento fletor no nó C, barra CD.
Dados para complementar a imagem: Carga 1: 12 KN/m; Carga 2: 14 KN/m; Carga 3: 8 KN/m.
Comprimento dos trechos: AB = 3 m; BC = 4 m e CD = 7 m.