RESISTÊNCIA DOS MATERIAIS
Um esquema de engrenagens, com base na ilustração abaixo, assinale a alternativa que contém o valor do torque no eixo 2.
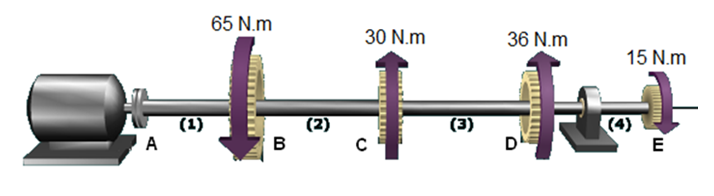
14 N.m
35 N.m
51 N.m
9 N.m
21 N.m
A viga é composta por três peças de plástico coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrada na figura, determine a tensão de cisalhamento desenvolvida nas juntas coladas na seção crítica. Os apoios em C e D exercem somente reações verticais sobre a viga.
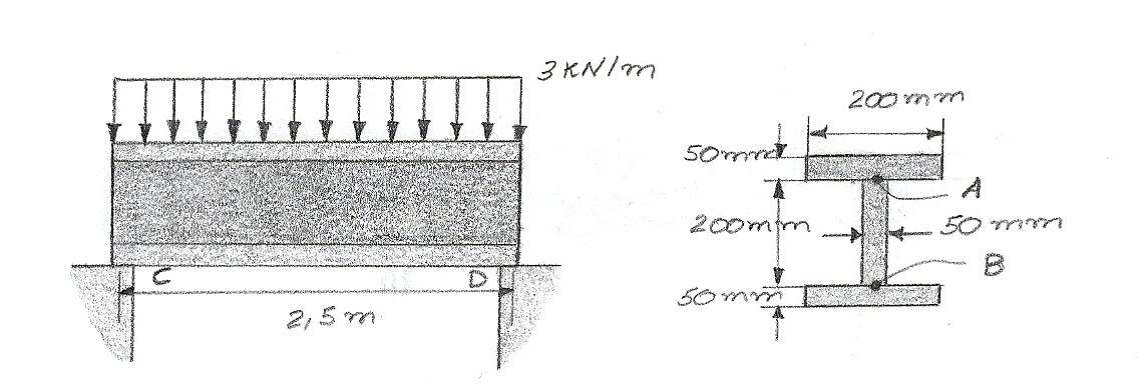
TA = TB = 0,268 MPa
TA = 14 MPa e TB = 26 MPa
TA = 48 MPa e TB = 26 MPa
TA = 0,148 MPa e TB = 0,268 MPa
TA = 148 MPa e TB = 268 MPa
Um cilindro de alumínio esta no interior de um tubo de aço e o conjunto é comprimido axialmente por 240 kN por intermédio de placas rígidas. O cilindro de alumínio tem 8 cm de diâmetro e o de aço tem 10 cm de diâmetro externo. Determine as tensões desenvolvidas no aço e no alumínio, e o coeficiente de segurança do sistema. Dados:
Alumínio aço
E = 0.28 . 104 kN/cm2 E = 2.1 . 104 kN/cm2
σ e = 6 kN/cm2 σe = 12 kN/cm2
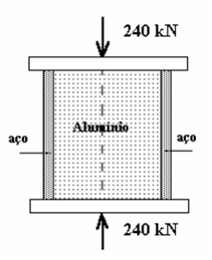
σaço = 6.85 kN/cm2; σAl = 0.91 kN/cm2; s = 1.65
σaço = 6.85 kN/cm2; σAl = 0.71 kN/cm2; s = 1.75
σaço = 6.85 kN/cm2; σAl = 0.71 kN/cm2; s = 1.65
σaço = 6.85 kN/cm2; σAl = 0.91 kN/cm2; s = 1.75
σaço = 8.65 kN/cm2; σAl = 0.91 kN/cm2; s = 1.75
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,84 MPa, determine a maior carga vertical P aplicada no centro que ele pode suportar.
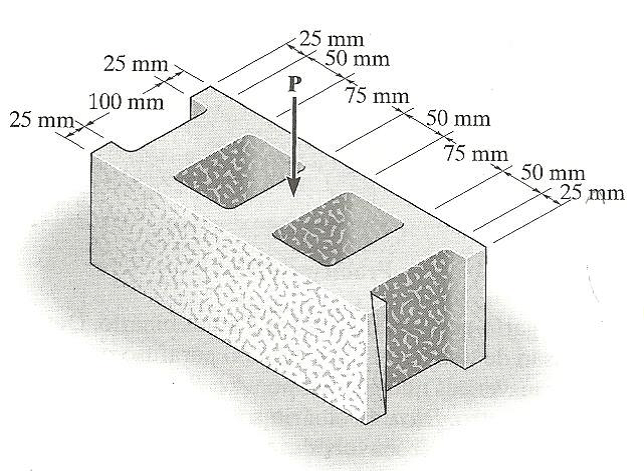
P = 29,3 KN
P = 27,3 KN
P = 25 KN
P = 23,7 KN
P = 21 KN
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine o maior torque T1 que pode ser aplicado ao eixo se ele também estiver sujeito a outros carregamentos de torção. Exige-se que T1 aja na direção mostrada.
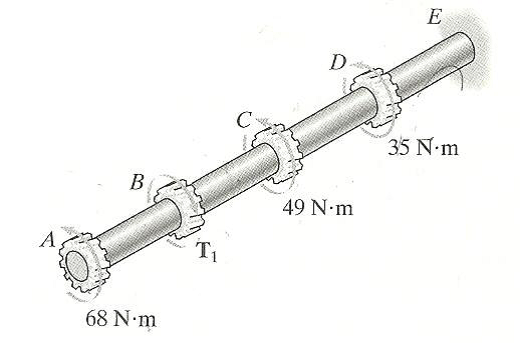
T1 = 7,74 N.m
T1 = 4,74 N.m
T1 = 8,74 N.m
T1 = 9,74 N.m
T1 = 3,74 N.m
A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.

Tmáx = 13,76 MPa
Tmáx = 14,74 MPa
Tmáx = 11,74 MPa
Tmáx = 15,64 MPa
Tmáx = 17,44 MPa
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga for deslocada 10 mm para baixo, determine a deformação normal desenvolvida nos cabos CE e BD.

Ece = 1,79 x 10-3 mm/mm; Ebd = 1,43 x 10-3 mm/mm
Ece = 1,43 x 10-3 mm/mm; Ebd = 1,79 x 10-3 mm/mm
Ece = 2,79 x 10-3 mm/mm; Ebd = 2,43 x 10-3 mm/mm
Ece = 1,97 x 10-3 mm/mm; Ebd = 1,63 x 10-3 mm/mm
Ece = 0,79 x 10-3 mm/mm; Ebd = 0,43 x 10-3 mm/mm
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se os parafusos estiverem espaçados de s = 200 mm, determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.


14 N.m
35 N.m
51 N.m
9 N.m
21 N.m
A viga é composta por três peças de plástico coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrada na figura, determine a tensão de cisalhamento desenvolvida nas juntas coladas na seção crítica. Os apoios em C e D exercem somente reações verticais sobre a viga.

TA = TB = 0,268 MPa
TA = 14 MPa e TB = 26 MPa
TA = 48 MPa e TB = 26 MPa
TA = 0,148 MPa e TB = 0,268 MPa
TA = 148 MPa e TB = 268 MPa
Um cilindro de alumínio esta no interior de um tubo de aço e o conjunto é comprimido axialmente por 240 kN por intermédio de placas rígidas. O cilindro de alumínio tem 8 cm de diâmetro e o de aço tem 10 cm de diâmetro externo. Determine as tensões desenvolvidas no aço e no alumínio, e o coeficiente de segurança do sistema. Dados:
Alumínio aço
E = 0.28 . 104 kN/cm2 E = 2.1 . 104 kN/cm2
σ e = 6 kN/cm2 σe = 12 kN/cm2

σaço = 6.85 kN/cm2; σAl = 0.91 kN/cm2; s = 1.65
σaço = 6.85 kN/cm2; σAl = 0.71 kN/cm2; s = 1.75
σaço = 6.85 kN/cm2; σAl = 0.71 kN/cm2; s = 1.65
σaço = 6.85 kN/cm2; σAl = 0.91 kN/cm2; s = 1.75
σaço = 8.65 kN/cm2; σAl = 0.91 kN/cm2; s = 1.75
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,84 MPa, determine a maior carga vertical P aplicada no centro que ele pode suportar.

P = 29,3 KN
P = 27,3 KN
P = 25 KN
P = 23,7 KN
P = 21 KN
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine o maior torque T1 que pode ser aplicado ao eixo se ele também estiver sujeito a outros carregamentos de torção. Exige-se que T1 aja na direção mostrada.

T1 = 7,74 N.m
T1 = 4,74 N.m
T1 = 8,74 N.m
T1 = 9,74 N.m
T1 = 3,74 N.m
A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.

Tmáx = 13,76 MPa
Tmáx = 14,74 MPa
Tmáx = 11,74 MPa
Tmáx = 15,64 MPa
Tmáx = 17,44 MPa
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga for deslocada 10 mm para baixo, determine a deformação normal desenvolvida nos cabos CE e BD.

Ece = 1,79 x 10-3 mm/mm; Ebd = 1,43 x 10-3 mm/mm
Ece = 1,43 x 10-3 mm/mm; Ebd = 1,79 x 10-3 mm/mm
Ece = 2,79 x 10-3 mm/mm; Ebd = 2,43 x 10-3 mm/mm
Ece = 1,97 x 10-3 mm/mm; Ebd = 1,63 x 10-3 mm/mm
Ece = 0,79 x 10-3 mm/mm; Ebd = 0,43 x 10-3 mm/mm
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se os parafusos estiverem espaçados de s = 200 mm, determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.


TA = TB = 0,268 MPa
TA = 14 MPa e TB = 26 MPa
TA = 48 MPa e TB = 26 MPa
TA = 0,148 MPa e TB = 0,268 MPa
TA = 148 MPa e TB = 268 MPa
Um cilindro de alumínio esta no interior de um tubo de aço e o conjunto é comprimido axialmente por 240 kN por intermédio de placas rígidas. O cilindro de alumínio tem 8 cm de diâmetro e o de aço tem 10 cm de diâmetro externo. Determine as tensões desenvolvidas no aço e no alumínio, e o coeficiente de segurança do sistema. Dados:
Alumínio aço
E = 0.28 . 104 kN/cm2 E = 2.1 . 104 kN/cm2
σ e = 6 kN/cm2 σe = 12 kN/cm2

σaço = 6.85 kN/cm2; σAl = 0.91 kN/cm2; s = 1.65
σaço = 6.85 kN/cm2; σAl = 0.71 kN/cm2; s = 1.75
σaço = 6.85 kN/cm2; σAl = 0.71 kN/cm2; s = 1.65
σaço = 6.85 kN/cm2; σAl = 0.91 kN/cm2; s = 1.75
σaço = 8.65 kN/cm2; σAl = 0.91 kN/cm2; s = 1.75
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,84 MPa, determine a maior carga vertical P aplicada no centro que ele pode suportar.

P = 29,3 KN
P = 27,3 KN
P = 25 KN
P = 23,7 KN
P = 21 KN
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine o maior torque T1 que pode ser aplicado ao eixo se ele também estiver sujeito a outros carregamentos de torção. Exige-se que T1 aja na direção mostrada.

T1 = 7,74 N.m
T1 = 4,74 N.m
T1 = 8,74 N.m
T1 = 9,74 N.m
T1 = 3,74 N.m
A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.

Tmáx = 13,76 MPa
Tmáx = 14,74 MPa
Tmáx = 11,74 MPa
Tmáx = 15,64 MPa
Tmáx = 17,44 MPa
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga for deslocada 10 mm para baixo, determine a deformação normal desenvolvida nos cabos CE e BD.

Ece = 1,79 x 10-3 mm/mm; Ebd = 1,43 x 10-3 mm/mm
Ece = 1,43 x 10-3 mm/mm; Ebd = 1,79 x 10-3 mm/mm
Ece = 2,79 x 10-3 mm/mm; Ebd = 2,43 x 10-3 mm/mm
Ece = 1,97 x 10-3 mm/mm; Ebd = 1,63 x 10-3 mm/mm
Ece = 0,79 x 10-3 mm/mm; Ebd = 0,43 x 10-3 mm/mm
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se os parafusos estiverem espaçados de s = 200 mm, determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.


σaço = 6.85 kN/cm2; σAl = 0.91 kN/cm2; s = 1.65
σaço = 6.85 kN/cm2; σAl = 0.71 kN/cm2; s = 1.75
σaço = 6.85 kN/cm2; σAl = 0.71 kN/cm2; s = 1.65
σaço = 6.85 kN/cm2; σAl = 0.91 kN/cm2; s = 1.75
σaço = 8.65 kN/cm2; σAl = 0.91 kN/cm2; s = 1.75
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,84 MPa, determine a maior carga vertical P aplicada no centro que ele pode suportar.

P = 29,3 KN
P = 27,3 KN
P = 25 KN
P = 23,7 KN
P = 21 KN
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine o maior torque T1 que pode ser aplicado ao eixo se ele também estiver sujeito a outros carregamentos de torção. Exige-se que T1 aja na direção mostrada.

T1 = 7,74 N.m
T1 = 4,74 N.m
T1 = 8,74 N.m
T1 = 9,74 N.m
T1 = 3,74 N.m
A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.

Tmáx = 13,76 MPa
Tmáx = 14,74 MPa
Tmáx = 11,74 MPa
Tmáx = 15,64 MPa
Tmáx = 17,44 MPa
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga for deslocada 10 mm para baixo, determine a deformação normal desenvolvida nos cabos CE e BD.

Ece = 1,79 x 10-3 mm/mm; Ebd = 1,43 x 10-3 mm/mm
Ece = 1,43 x 10-3 mm/mm; Ebd = 1,79 x 10-3 mm/mm
Ece = 2,79 x 10-3 mm/mm; Ebd = 2,43 x 10-3 mm/mm
Ece = 1,97 x 10-3 mm/mm; Ebd = 1,63 x 10-3 mm/mm
Ece = 0,79 x 10-3 mm/mm; Ebd = 0,43 x 10-3 mm/mm
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se os parafusos estiverem espaçados de s = 200 mm, determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.


P = 29,3 KN
P = 27,3 KN
P = 25 KN
P = 23,7 KN
P = 21 KN
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine o maior torque T1 que pode ser aplicado ao eixo se ele também estiver sujeito a outros carregamentos de torção. Exige-se que T1 aja na direção mostrada.

T1 = 7,74 N.m
T1 = 4,74 N.m
T1 = 8,74 N.m
T1 = 9,74 N.m
T1 = 3,74 N.m
A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.

Tmáx = 13,76 MPa
Tmáx = 14,74 MPa
Tmáx = 11,74 MPa
Tmáx = 15,64 MPa
Tmáx = 17,44 MPa
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga for deslocada 10 mm para baixo, determine a deformação normal desenvolvida nos cabos CE e BD.

Ece = 1,79 x 10-3 mm/mm; Ebd = 1,43 x 10-3 mm/mm
Ece = 1,43 x 10-3 mm/mm; Ebd = 1,79 x 10-3 mm/mm
Ece = 2,79 x 10-3 mm/mm; Ebd = 2,43 x 10-3 mm/mm
Ece = 1,97 x 10-3 mm/mm; Ebd = 1,63 x 10-3 mm/mm
Ece = 0,79 x 10-3 mm/mm; Ebd = 0,43 x 10-3 mm/mm
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se os parafusos estiverem espaçados de s = 200 mm, determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.


T1 = 7,74 N.m
T1 = 4,74 N.m
T1 = 8,74 N.m
T1 = 9,74 N.m
T1 = 3,74 N.m
A viga T está sujeita ao carregamento mostrado na figura. Determine a tensão de cisalhamento transversal máxima na seção crítica da viga.

Tmáx = 13,76 MPa
Tmáx = 14,74 MPa
Tmáx = 11,74 MPa
Tmáx = 15,64 MPa
Tmáx = 17,44 MPa
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga for deslocada 10 mm para baixo, determine a deformação normal desenvolvida nos cabos CE e BD.

Ece = 1,79 x 10-3 mm/mm; Ebd = 1,43 x 10-3 mm/mm
Ece = 1,43 x 10-3 mm/mm; Ebd = 1,79 x 10-3 mm/mm
Ece = 2,79 x 10-3 mm/mm; Ebd = 2,43 x 10-3 mm/mm
Ece = 1,97 x 10-3 mm/mm; Ebd = 1,63 x 10-3 mm/mm
Ece = 0,79 x 10-3 mm/mm; Ebd = 0,43 x 10-3 mm/mm
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se os parafusos estiverem espaçados de s = 200 mm, determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.

Tmáx = 13,76 MPa
Tmáx = 14,74 MPa
Tmáx = 11,74 MPa
Tmáx = 15,64 MPa
Tmáx = 17,44 MPa
A viga rígida é sustentada por um pino em A e pelos cabos BD e CE. Se a carga P aplicada à viga for deslocada 10 mm para baixo, determine a deformação normal desenvolvida nos cabos CE e BD.

Ece = 1,79 x 10-3 mm/mm; Ebd = 1,43 x 10-3 mm/mm
Ece = 1,43 x 10-3 mm/mm; Ebd = 1,79 x 10-3 mm/mm
Ece = 2,79 x 10-3 mm/mm; Ebd = 2,43 x 10-3 mm/mm
Ece = 1,97 x 10-3 mm/mm; Ebd = 1,63 x 10-3 mm/mm
Ece = 0,79 x 10-3 mm/mm; Ebd = 0,43 x 10-3 mm/mm
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se os parafusos estiverem espaçados de s = 200 mm, determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.

Ece = 1,79 x 10-3 mm/mm; Ebd = 1,43 x 10-3 mm/mm
Ece = 1,43 x 10-3 mm/mm; Ebd = 1,79 x 10-3 mm/mm
Ece = 2,79 x 10-3 mm/mm; Ebd = 2,43 x 10-3 mm/mm
Ece = 1,97 x 10-3 mm/mm; Ebd = 1,63 x 10-3 mm/mm
Ece = 0,79 x 10-3 mm/mm; Ebd = 0,43 x 10-3 mm/mm
A viga é fabricada com dois T estruturais equivalentes e duas chapas. Cada chapa tem altura de 150 mm e espessura de 12 mm. Se os parafusos estiverem espaçados de s = 200 mm, determine a força de cisalhamento máxima V que pode ser aplicada à seção transversal. Cada parafuso pode resistir a uma força de cisalhamento de 75 kN.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.

V = 175,2 kN
V = 152,5 kN
V = 172,5 kN
V = 157,5 kN
V = 127,5 kN
Os cantos da chapa quadrada sofrem os deslocamentos indicados. Determine a deformação por cisalhamento ao longo das bordas da chapa em A e B.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad
Determine a resultante das forças internas normal e de cisalhamento no elemento na seção a-a e na seção b-b, sendo que cada uma delas passa pelo ponto A. Considerando θ = 60°. A carga de 650 N é aplicada ao longo do eixo do centroide do elemento.

ϒa = 0,02024 rad; ϒb = 0,02024 rad
ϒa = 0,05024 rad; ϒb = 0,05024 rad
ϒa = 0,04054 rad; ϒb = 0,04054 rad
ϒa = 0,05024 rad; ϒb = 0,04054 rad
ϒa = 0,03024 rad; ϒb = 0,03024 rad