RESISTÊNCIA DOS MATERIAIS
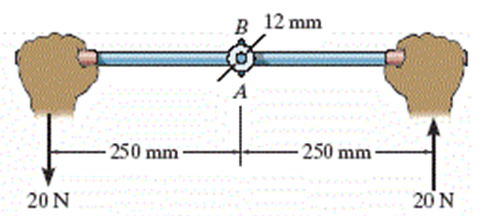
A alavanca está presa ao eixo fixo por um pino cônico AB, cujo diâmetro médio é 6 mm. Se um binário for aplicado à alavanca, determine a tensão de cisalhamento média no pino entre ele e a alavanca.
5,63 MPa
29,47 MPa
45,32 MPa
18,65 MPa
3,45 MPa
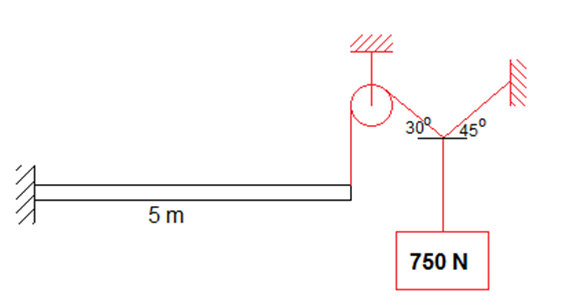
Determinar o deslocamento (deflexão) máximo que corre na viga a seguir.
y = 552.8/EI
y = 6910/EI
y = 276.4/EI
y = 23033.75/EI
y = 677.44/EI
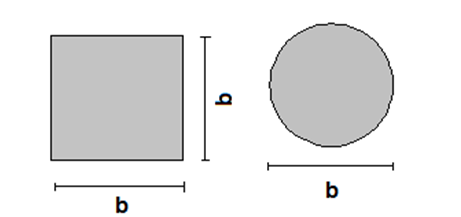
Os eixos A e B são feitos de mesmo material e têm seção transversal conforme indicada na figura, de mesma dimensão “b”. Qual é a relação entre os máximos torques T que podem ser aplicados na seção quadrada e na seção circular (T quadrado/ T circunferência)?

0,50
2,10
0,95
1,40
1,06
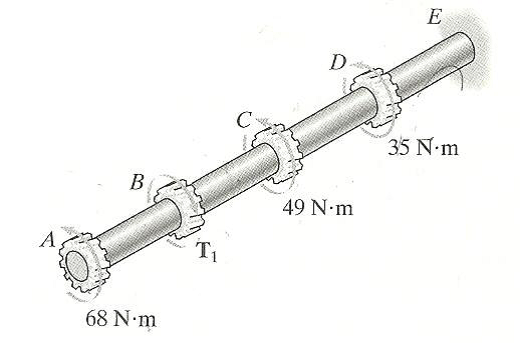
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine a tensão de cisalhamento máxima no interior das regiões DE . Exige-se que T1 aja na direção mostrada.
TDE = 6 MPa
TDE = 8 MPa
TDE = 4,6 MPa
TDE = 4,74 MPa
TDE = 6,75 MPa
Determine as cargas internas resultantes que agem na seção transversal da estrutura nos pontos F e G. O contato em E é liso.
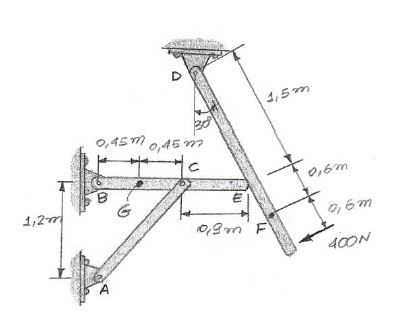
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 16 N.m; NG = 83,54 N; VG = 36 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 183,54 N; VG = 160 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 83,54 N; VG = 360 N
MF = 240 N.m; NF = 0 N; VF = 40 N; MG = - 102 N.m; NG = 83,54 N; VG = 360 N
MF = 140 N.m; NF = 0 N; VF = 200 N; MG = - 162 N.m; NG = 80,54 N; VG = 160 N
Um edifício de porte alto terá no pavimento térreo uma coluna maciça de concreto armado com diâmetro de 1,80m, sendo sua base engastada em fundação profunda e articulado a uma viga na extremidade superior. A coluna foi calculada à compressão para uma tensão admissível σad =20 MPa e deseja-se obter um coeficiente de segurança à flambagem igual a 3,0. Para estas condições pede-se o cálculo da altura da coluna.
Dado: E = 300 Tf/cm²
L = 23,7 m
L = 21,5 m
L = 22,4 m
L = 25,2 m
L = 23,9 m
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.


5,63 MPa
29,47 MPa
45,32 MPa
18,65 MPa
3,45 MPa
Determinar o deslocamento (deflexão) máximo que corre na viga a seguir.

y = 552.8/EI
y = 6910/EI
y = 276.4/EI
y = 23033.75/EI
y = 677.44/EI
Os eixos A e B são feitos de mesmo material e têm seção transversal conforme indicada na figura, de mesma dimensão “b”. Qual é a relação entre os máximos torques T que podem ser aplicados na seção quadrada e na seção circular (T quadrado/ T circunferência)?


0,50
2,10
0,95
1,40
1,06
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine a tensão de cisalhamento máxima no interior das regiões DE . Exige-se que T1 aja na direção mostrada.

TDE = 6 MPa
TDE = 8 MPa
TDE = 4,6 MPa
TDE = 4,74 MPa
TDE = 6,75 MPa
Determine as cargas internas resultantes que agem na seção transversal da estrutura nos pontos F e G. O contato em E é liso.

MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 16 N.m; NG = 83,54 N; VG = 36 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 183,54 N; VG = 160 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 83,54 N; VG = 360 N
MF = 240 N.m; NF = 0 N; VF = 40 N; MG = - 102 N.m; NG = 83,54 N; VG = 360 N
MF = 140 N.m; NF = 0 N; VF = 200 N; MG = - 162 N.m; NG = 80,54 N; VG = 160 N
Um edifício de porte alto terá no pavimento térreo uma coluna maciça de concreto armado com diâmetro de 1,80m, sendo sua base engastada em fundação profunda e articulado a uma viga na extremidade superior. A coluna foi calculada à compressão para uma tensão admissível σad =20 MPa e deseja-se obter um coeficiente de segurança à flambagem igual a 3,0. Para estas condições pede-se o cálculo da altura da coluna.
Dado: E = 300 Tf/cm²
L = 23,7 m
L = 21,5 m
L = 22,4 m
L = 25,2 m
L = 23,9 m
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.


y = 552.8/EI
y = 6910/EI
y = 276.4/EI
y = 23033.75/EI
y = 677.44/EI
Os eixos A e B são feitos de mesmo material e têm seção transversal conforme indicada na figura, de mesma dimensão “b”. Qual é a relação entre os máximos torques T que podem ser aplicados na seção quadrada e na seção circular (T quadrado/ T circunferência)?


0,50
2,10
0,95
1,40
1,06
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine a tensão de cisalhamento máxima no interior das regiões DE . Exige-se que T1 aja na direção mostrada.

TDE = 6 MPa
TDE = 8 MPa
TDE = 4,6 MPa
TDE = 4,74 MPa
TDE = 6,75 MPa
Determine as cargas internas resultantes que agem na seção transversal da estrutura nos pontos F e G. O contato em E é liso.

MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 16 N.m; NG = 83,54 N; VG = 36 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 183,54 N; VG = 160 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 83,54 N; VG = 360 N
MF = 240 N.m; NF = 0 N; VF = 40 N; MG = - 102 N.m; NG = 83,54 N; VG = 360 N
MF = 140 N.m; NF = 0 N; VF = 200 N; MG = - 162 N.m; NG = 80,54 N; VG = 160 N
Um edifício de porte alto terá no pavimento térreo uma coluna maciça de concreto armado com diâmetro de 1,80m, sendo sua base engastada em fundação profunda e articulado a uma viga na extremidade superior. A coluna foi calculada à compressão para uma tensão admissível σad =20 MPa e deseja-se obter um coeficiente de segurança à flambagem igual a 3,0. Para estas condições pede-se o cálculo da altura da coluna.
Dado: E = 300 Tf/cm²
L = 23,7 m
L = 21,5 m
L = 22,4 m
L = 25,2 m
L = 23,9 m
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.


0,50
2,10
0,95
1,40
1,06
O eixo maciço de alumínio tem diâmetro de 50 mm e tensão de cisalhamento admissível τadm = 6 MPa. Determine a tensão de cisalhamento máxima no interior das regiões DE . Exige-se que T1 aja na direção mostrada.

TDE = 6 MPa
TDE = 8 MPa
TDE = 4,6 MPa
TDE = 4,74 MPa
TDE = 6,75 MPa
Determine as cargas internas resultantes que agem na seção transversal da estrutura nos pontos F e G. O contato em E é liso.

MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 16 N.m; NG = 83,54 N; VG = 36 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 183,54 N; VG = 160 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 83,54 N; VG = 360 N
MF = 240 N.m; NF = 0 N; VF = 40 N; MG = - 102 N.m; NG = 83,54 N; VG = 360 N
MF = 140 N.m; NF = 0 N; VF = 200 N; MG = - 162 N.m; NG = 80,54 N; VG = 160 N
Um edifício de porte alto terá no pavimento térreo uma coluna maciça de concreto armado com diâmetro de 1,80m, sendo sua base engastada em fundação profunda e articulado a uma viga na extremidade superior. A coluna foi calculada à compressão para uma tensão admissível σad =20 MPa e deseja-se obter um coeficiente de segurança à flambagem igual a 3,0. Para estas condições pede-se o cálculo da altura da coluna.
Dado: E = 300 Tf/cm²
L = 23,7 m
L = 21,5 m
L = 22,4 m
L = 25,2 m
L = 23,9 m
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.


TDE = 6 MPa
TDE = 8 MPa
TDE = 4,6 MPa
TDE = 4,74 MPa
TDE = 6,75 MPa
Determine as cargas internas resultantes que agem na seção transversal da estrutura nos pontos F e G. O contato em E é liso.

MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 16 N.m; NG = 83,54 N; VG = 36 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 183,54 N; VG = 160 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 83,54 N; VG = 360 N
MF = 240 N.m; NF = 0 N; VF = 40 N; MG = - 102 N.m; NG = 83,54 N; VG = 360 N
MF = 140 N.m; NF = 0 N; VF = 200 N; MG = - 162 N.m; NG = 80,54 N; VG = 160 N
Um edifício de porte alto terá no pavimento térreo uma coluna maciça de concreto armado com diâmetro de 1,80m, sendo sua base engastada em fundação profunda e articulado a uma viga na extremidade superior. A coluna foi calculada à compressão para uma tensão admissível σad =20 MPa e deseja-se obter um coeficiente de segurança à flambagem igual a 3,0. Para estas condições pede-se o cálculo da altura da coluna.
Dado: E = 300 Tf/cm²
L = 23,7 m
L = 21,5 m
L = 22,4 m
L = 25,2 m
L = 23,9 m
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.


MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 16 N.m; NG = 83,54 N; VG = 36 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 183,54 N; VG = 160 N
MF = 240 N.m; NF = 0 N; VF = 400 N; MG = - 162 N.m; NG = 83,54 N; VG = 360 N
MF = 240 N.m; NF = 0 N; VF = 40 N; MG = - 102 N.m; NG = 83,54 N; VG = 360 N
MF = 140 N.m; NF = 0 N; VF = 200 N; MG = - 162 N.m; NG = 80,54 N; VG = 160 N
Um edifício de porte alto terá no pavimento térreo uma coluna maciça de concreto armado com diâmetro de 1,80m, sendo sua base engastada em fundação profunda e articulado a uma viga na extremidade superior. A coluna foi calculada à compressão para uma tensão admissível σad =20 MPa e deseja-se obter um coeficiente de segurança à flambagem igual a 3,0. Para estas condições pede-se o cálculo da altura da coluna.
Dado: E = 300 Tf/cm²
L = 23,7 m
L = 21,5 m
L = 22,4 m
L = 25,2 m
L = 23,9 m
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.

L = 23,7 m
L = 21,5 m
L = 22,4 m
L = 25,2 m
L = 23,9 m
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
Se a força P = 4 kN, determine a tensão de cisalhamento máxima na seção crítica da viga. Os apoios em A e B exercem somente reações verticais sobre a viga.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.

Tmáx = 0,750 MPa
Tmáx = 1,250 MPa
Tmáx = 0,650 MPa
Tmáx = 0,850 MPa
Tmáx = 0,550 MPa
A coluna de aço suporta as duas cargas excêntricas. Se considerarmos que ela está engastada no topo e na base e totalmente escorada contra flambagem em torno do eixo y-y, determine a tensão máxima da coluna. . Eaço = 200 GPA, σe = 360 GPA.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa
O diagrama tensão-deformação para o polietileno que é utilizado para revestir cabos coaxiais é determinado por um ensaio com um corpo de prova com comprimento de referência de 250 mm. Se uma carga P aplicada ao corpo de prova desenvolver uma deformação ε = 0,024 mm/mm, determine o valor aproximado do comprimento do corpo de prova medido entre os pontos de referência quando a carga é removida. Considere que o corpo de prova se recupere elasticamente.

σmax = 77,4 Mpa
σmax = 177.7 Mpa
σmax = 1,47 Mpa
σmax = 27,74 Mpa
σmax = 17,74 Mpa