PRÉ-CÁLCULO
Quantas voltas completas dá, e em que quadrante pára um móvel que, partindo da origem dos arcos, percorre um arco de 1810º?
3 voltas e pára no segundo quadrante.
4 voltas e pára no terceiro quadrante
6 voltas e pára no quarto quadrante.
7 voltas e pára no primeiro quadrante.
5 voltas e pára no primeiro quadrante.
Considerando o arco igual 2100º, qual será a sua determinação principal?
O arco possui determinação principal no 3º quadrante , com 5 voltas completas.
O arco possui determinação principal no 4º quadrante , com 5 voltas completas.
O arco possui determinação principal no 2º quadrante , com 6 voltas completas.
O arco possui determinação principal no 1º quadrante , com 6 voltas completas.
O arco possui determinação principal no 3º quadrante, com 4 voltas completas.
Uma pessoa completou quatro voltas em torno de uma praça circular de 20m de raio. Podemos afirmar que a pessoa caminhou
Adote pi = 3,14
600,2m
628m
464,6m
502,4m
396,2m
No item abaixo, utilize as relações entre os ângulos formados por retas paralelas cortadas por uma transversal e calcule o valor de x, em seguida marque a alternativa correta.
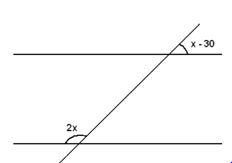
120°
70°
150°
90°
80°
As bases de um trapézio isóceles ABCD (representado na figura) medem 50 cm e 30 cm. A altura desse trapézio é de 10 cm. Prolongando-se os lados não-paralelos, eles se interceptam em um ponto E. Marque a opção que apresenta a altura CORRETA, em centímetros, do triângulo ABE.
25 cm
20 cm
16 cm
15 cm
12 cm
Sobre os lados AB e AC do triângulo ABC, são marcados os pontos D e E , respectivamente, de tal forma, que DE // BC, AE = 6 cm, DB = 2 cm, EC = 3 cm e DE = 8 cm. Nessas condições, a soma das medidas dos segmentos AD e BC, em centímetros, vale:
12
24
18
30
16
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere Q = C.1,25 2 - 0,125.t, a quantidade Q de substância em miligramas que permanece no paciente, t horas após a aplicação. C é a quantidade no início da aplicação (t=0). A quantidade de substância em miligramas que permanece no paciente após 8 horas se C = 15 é aproximadamente
17,15
16,55
19,95
18,75
16,99
O número de bactérias de uma determinada cultura é dado pela expressão B(t) = 1100 . 20,3t, em que B(t) é o número de bactérias em função do tempo e t é o tempo em anos.
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10
Considere que a expressão H(t) = P0 . 20, 05t fornece o número H de habitantes de uma determinada região, em função do tempo t em anos. Se hoje a população inicial P0 é exatamente 500 000 habitantes, é certo afirmar que daqui a 20 anos teremos uma população igual a:
3 voltas e pára no segundo quadrante.
4 voltas e pára no terceiro quadrante
6 voltas e pára no quarto quadrante.
7 voltas e pára no primeiro quadrante.
5 voltas e pára no primeiro quadrante.
Considerando o arco igual 2100º, qual será a sua determinação principal?
O arco possui determinação principal no 3º quadrante , com 5 voltas completas.
O arco possui determinação principal no 4º quadrante , com 5 voltas completas.
O arco possui determinação principal no 2º quadrante , com 6 voltas completas.
O arco possui determinação principal no 1º quadrante , com 6 voltas completas.
O arco possui determinação principal no 3º quadrante, com 4 voltas completas.
Uma pessoa completou quatro voltas em torno de uma praça circular de 20m de raio. Podemos afirmar que a pessoa caminhou
Adote pi = 3,14
600,2m
628m
464,6m
502,4m
396,2m
No item abaixo, utilize as relações entre os ângulos formados por retas paralelas cortadas por uma transversal e calcule o valor de x, em seguida marque a alternativa correta.

120°
70°
150°
90°
80°
As bases de um trapézio isóceles ABCD (representado na figura) medem 50 cm e 30 cm. A altura desse trapézio é de 10 cm. Prolongando-se os lados não-paralelos, eles se interceptam em um ponto E. Marque a opção que apresenta a altura CORRETA, em centímetros, do triângulo ABE.
25 cm
20 cm
16 cm
15 cm
12 cm
Sobre os lados AB e AC do triângulo ABC, são marcados os pontos D e E , respectivamente, de tal forma, que DE // BC, AE = 6 cm, DB = 2 cm, EC = 3 cm e DE = 8 cm. Nessas condições, a soma das medidas dos segmentos AD e BC, em centímetros, vale:
12
24
18
30
16
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere Q = C.1,25 2 - 0,125.t, a quantidade Q de substância em miligramas que permanece no paciente, t horas após a aplicação. C é a quantidade no início da aplicação (t=0). A quantidade de substância em miligramas que permanece no paciente após 8 horas se C = 15 é aproximadamente
17,15
16,55
19,95
18,75
16,99
O número de bactérias de uma determinada cultura é dado pela expressão B(t) = 1100 . 20,3t, em que B(t) é o número de bactérias em função do tempo e t é o tempo em anos.
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10
Considere que a expressão H(t) = P0 . 20, 05t fornece o número H de habitantes de uma determinada região, em função do tempo t em anos. Se hoje a população inicial P0 é exatamente 500 000 habitantes, é certo afirmar que daqui a 20 anos teremos uma população igual a:
O arco possui determinação principal no 3º quadrante , com 5 voltas completas.
O arco possui determinação principal no 4º quadrante , com 5 voltas completas.
O arco possui determinação principal no 2º quadrante , com 6 voltas completas.
O arco possui determinação principal no 1º quadrante , com 6 voltas completas.
O arco possui determinação principal no 3º quadrante, com 4 voltas completas.
Uma pessoa completou quatro voltas em torno de uma praça circular de 20m de raio. Podemos afirmar que a pessoa caminhou
Adote pi = 3,14
600,2m
628m
464,6m
502,4m
396,2m
No item abaixo, utilize as relações entre os ângulos formados por retas paralelas cortadas por uma transversal e calcule o valor de x, em seguida marque a alternativa correta.

120°
70°
150°
90°
80°
As bases de um trapézio isóceles ABCD (representado na figura) medem 50 cm e 30 cm. A altura desse trapézio é de 10 cm. Prolongando-se os lados não-paralelos, eles se interceptam em um ponto E. Marque a opção que apresenta a altura CORRETA, em centímetros, do triângulo ABE.
25 cm
20 cm
16 cm
15 cm
12 cm
Sobre os lados AB e AC do triângulo ABC, são marcados os pontos D e E , respectivamente, de tal forma, que DE // BC, AE = 6 cm, DB = 2 cm, EC = 3 cm e DE = 8 cm. Nessas condições, a soma das medidas dos segmentos AD e BC, em centímetros, vale:
12
24
18
30
16
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere Q = C.1,25 2 - 0,125.t, a quantidade Q de substância em miligramas que permanece no paciente, t horas após a aplicação. C é a quantidade no início da aplicação (t=0). A quantidade de substância em miligramas que permanece no paciente após 8 horas se C = 15 é aproximadamente
17,15
16,55
19,95
18,75
16,99
O número de bactérias de uma determinada cultura é dado pela expressão B(t) = 1100 . 20,3t, em que B(t) é o número de bactérias em função do tempo e t é o tempo em anos.
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10
Considere que a expressão H(t) = P0 . 20, 05t fornece o número H de habitantes de uma determinada região, em função do tempo t em anos. Se hoje a população inicial P0 é exatamente 500 000 habitantes, é certo afirmar que daqui a 20 anos teremos uma população igual a:
600,2m
628m
464,6m
502,4m
396,2m
No item abaixo, utilize as relações entre os ângulos formados por retas paralelas cortadas por uma transversal e calcule o valor de x, em seguida marque a alternativa correta.

120°
70°
150°
90°
80°
As bases de um trapézio isóceles ABCD (representado na figura) medem 50 cm e 30 cm. A altura desse trapézio é de 10 cm. Prolongando-se os lados não-paralelos, eles se interceptam em um ponto E. Marque a opção que apresenta a altura CORRETA, em centímetros, do triângulo ABE.
25 cm
20 cm
16 cm
15 cm
12 cm
Sobre os lados AB e AC do triângulo ABC, são marcados os pontos D e E , respectivamente, de tal forma, que DE // BC, AE = 6 cm, DB = 2 cm, EC = 3 cm e DE = 8 cm. Nessas condições, a soma das medidas dos segmentos AD e BC, em centímetros, vale:
12
24
18
30
16
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere Q = C.1,25 2 - 0,125.t, a quantidade Q de substância em miligramas que permanece no paciente, t horas após a aplicação. C é a quantidade no início da aplicação (t=0). A quantidade de substância em miligramas que permanece no paciente após 8 horas se C = 15 é aproximadamente
17,15
16,55
19,95
18,75
16,99
O número de bactérias de uma determinada cultura é dado pela expressão B(t) = 1100 . 20,3t, em que B(t) é o número de bactérias em função do tempo e t é o tempo em anos.
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10
Considere que a expressão H(t) = P0 . 20, 05t fornece o número H de habitantes de uma determinada região, em função do tempo t em anos. Se hoje a população inicial P0 é exatamente 500 000 habitantes, é certo afirmar que daqui a 20 anos teremos uma população igual a:

120°
70°
150°
90°
80°
As bases de um trapézio isóceles ABCD (representado na figura) medem 50 cm e 30 cm. A altura desse trapézio é de 10 cm. Prolongando-se os lados não-paralelos, eles se interceptam em um ponto E. Marque a opção que apresenta a altura CORRETA, em centímetros, do triângulo ABE.
25 cm
20 cm
16 cm
15 cm
12 cm
Sobre os lados AB e AC do triângulo ABC, são marcados os pontos D e E , respectivamente, de tal forma, que DE // BC, AE = 6 cm, DB = 2 cm, EC = 3 cm e DE = 8 cm. Nessas condições, a soma das medidas dos segmentos AD e BC, em centímetros, vale:
12
24
18
30
16
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere Q = C.1,25 2 - 0,125.t, a quantidade Q de substância em miligramas que permanece no paciente, t horas após a aplicação. C é a quantidade no início da aplicação (t=0). A quantidade de substância em miligramas que permanece no paciente após 8 horas se C = 15 é aproximadamente
17,15
16,55
19,95
18,75
16,99
O número de bactérias de uma determinada cultura é dado pela expressão B(t) = 1100 . 20,3t, em que B(t) é o número de bactérias em função do tempo e t é o tempo em anos.
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10
Considere que a expressão H(t) = P0 . 20, 05t fornece o número H de habitantes de uma determinada região, em função do tempo t em anos. Se hoje a população inicial P0 é exatamente 500 000 habitantes, é certo afirmar que daqui a 20 anos teremos uma população igual a:

25 cm
20 cm
16 cm
15 cm
12 cm
Sobre os lados AB e AC do triângulo ABC, são marcados os pontos D e E , respectivamente, de tal forma, que DE // BC, AE = 6 cm, DB = 2 cm, EC = 3 cm e DE = 8 cm. Nessas condições, a soma das medidas dos segmentos AD e BC, em centímetros, vale:
12
24
18
30
16
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere Q = C.1,25 2 - 0,125.t, a quantidade Q de substância em miligramas que permanece no paciente, t horas após a aplicação. C é a quantidade no início da aplicação (t=0). A quantidade de substância em miligramas que permanece no paciente após 8 horas se C = 15 é aproximadamente
17,15
16,55
19,95
18,75
16,99
O número de bactérias de uma determinada cultura é dado pela expressão B(t) = 1100 . 20,3t, em que B(t) é o número de bactérias em função do tempo e t é o tempo em anos.
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10
Considere que a expressão H(t) = P0 . 20, 05t fornece o número H de habitantes de uma determinada região, em função do tempo t em anos. Se hoje a população inicial P0 é exatamente 500 000 habitantes, é certo afirmar que daqui a 20 anos teremos uma população igual a:
12
24
18
30
16
Um tratamento médico consiste na aplicação de uma determinada substância a um paciente. Considere Q = C.1,25 2 - 0,125.t, a quantidade Q de substância em miligramas que permanece no paciente, t horas após a aplicação. C é a quantidade no início da aplicação (t=0). A quantidade de substância em miligramas que permanece no paciente após 8 horas se C = 15 é aproximadamente
17,15
16,55
19,95
18,75
16,99
O número de bactérias de uma determinada cultura é dado pela expressão B(t) = 1100 . 20,3t, em que B(t) é o número de bactérias em função do tempo e t é o tempo em anos.
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10
Considere que a expressão H(t) = P0 . 20, 05t fornece o número H de habitantes de uma determinada região, em função do tempo t em anos. Se hoje a população inicial P0 é exatamente 500 000 habitantes, é certo afirmar que daqui a 20 anos teremos uma população igual a:
17,15
16,55
19,95
18,75
16,99
O número de bactérias de uma determinada cultura é dado pela expressão B(t) = 1100 . 20,3t, em que B(t) é o número de bactérias em função do tempo e t é o tempo em anos.
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10
Considere que a expressão H(t) = P0 . 20, 05t fornece o número H de habitantes de uma determinada região, em função do tempo t em anos. Se hoje a população inicial P0 é exatamente 500 000 habitantes, é certo afirmar que daqui a 20 anos teremos uma população igual a:
O tempo em anos, necessário após o início do experimento para que a cultura tenha 563 200 bactérias será exatamente:
40
50
20
30
10