OBRAS DE TERRA
A barragem de terra indicada na figura abaixo será projetada para alcançar altura H de 9 metros. O talude a montante terá inclinação de 1:2,3, enquanto a inclinação do talude a jusante será 1:2,0. Dessa forma, dimensione as larguras de crista e de base da barragem, em metros. Adotar apenas uma casa após a vírgula, se necessário.
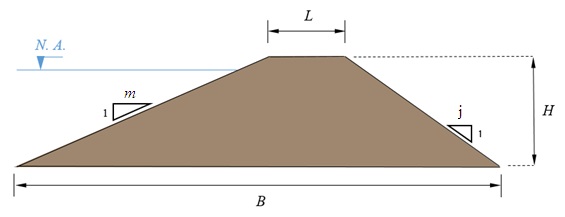
L = 4,3 m; B = 41,5 m.
L = 5,3 m; B = 52,5 m.
L = 4,8 m; B = 43,5 m.
L = 5 m; B = 50 m.
L = 4 m; B = 40 m.
Na verificação de um muro de arrimo, seja qual for a sua seção, devem ser investigadas quais condições de estabilidade?
Empuxo, equilíbrio estático, tombamento e sobrecarga.
Deslizamento da base, tombamento, capacidade de carga e ruptura global.
Ruptura global, coeficiente de segurança, empuxo e capacidade de carga.
Cisalhamento, empuxo, tombamento e sobrecarga.
Empuxo ativo, empuxo passivo, deslizamento da base e equilíbrio estático.
Sabendo que um muro de arrimo feito em alvenaria de tijolos com seção retangular deve vencer uma altura de 5,5 metros, é correto afirmar que o dimensionamento do topo equivale a:
234 cm.
220 cm.
165 cm.
184 cm.
275 cm.
Nas análises pelo Método de Culmann, os taludes são considerados como finitos, sendo a altura crítica associada ao plano crítico do talude. O plano crítico de um talude possui a menor relação entre a tensão média de cisalhamento, que tende a provocar a ruptura, e a resistência ao cisalhamento do solo. Com base nessas informações, calcule a altura crítica para o talude indicado de acordo com o Método de Culmann, em metros.
O talude possui as seguintes propriedades: φ = 14°; β = 32°; γ = 1,6 tf/m³; c' = 1 tf/m².
Em caso de resposta decimal, considerar uma casa após a virgula.
24,5 m
26,3 m
22,8 m
29,3 m
19,4 m
Considerando os efeitos da sobrecarga, calcule a altura equivalente de uma camada de solo, em metros. O peso específico do solo é de 2 t/m³, e a pressão aplicada é de 3,0 t/m². Sabe-se que q = (γ.h).
2,5 m
2 m
1,5 m
1 m
6 m
O ensaio de palheta é também conhecido como vane test, em que é possível obter a resistência não drenada da argila (Su), e é obtido admitindo-se que a ruptura se dá na superfície do cilindro, onde o torque necessário para causar a ruptura é medido. Realizado esse ensaio em um solo onde foram obtidas as informações apresentadas a seguir, determine a coesão do material (Su), em kg/cm². Dados: D = 6,6 cm; H = 11 cm; M = 645 kg.cm. Em caso de resposta decimal, considere duas casas após a vírgula.
Considere a fórmula indicada a seguir:
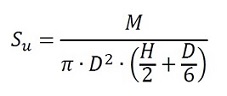
0,52 kg/cm²
0,95 kg/cm²
1,04 kg/cm²
0,39 kg/cm²
0,71 kg/cm²
Como o solo é um sistema particulado composto de partículas sólidas e espaços vazios, os quais podem estar parcial ou totalmente preenchidos com água, podemos afirmar que estão corretas apenas as afirmativas:
I. Uma das causas do decréscimo de volume é a compressão das partículas sólidas.
II. As deformações que ocorrem na água e nos grãos sólidos são desprezadas (pois são incompressíveis), calculando-se, portanto, apenas as deformações volumétricas do solo a partir da variação do índice de vazios.
III. As deformações ocorridas sempre serão uniformes, o que acarreta diretamente danos às estruturas assentes sobre o solo de fundação, o que inviabiliza a sua utilização.
Todas estão incorretas.
I e III.
II e III.
Todas estão corretas.
I e II.
Uma camada de argila saturada com 6,0 m de espessura, drenada por ambas as faces, apresenta as seguintes características: índice de vazios inicial igual a 1,02 e índice de compressão igual a 0,23. Determine o recalque primário da camada de argila, admitindo-se que essa sofra um acréscimo de tensões de 0,5 kg/cm².
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).
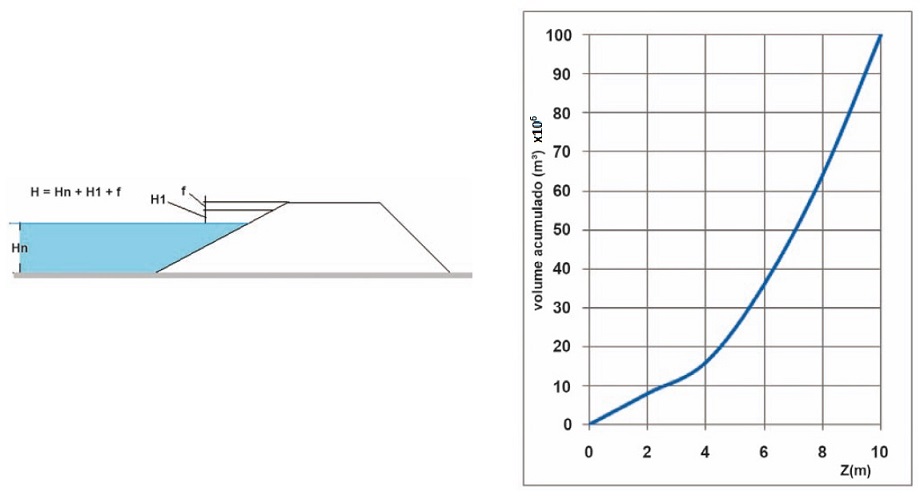
Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?

L = 4,3 m; B = 41,5 m.
L = 5,3 m; B = 52,5 m.
L = 4,8 m; B = 43,5 m.
L = 5 m; B = 50 m.
L = 4 m; B = 40 m.
Na verificação de um muro de arrimo, seja qual for a sua seção, devem ser investigadas quais condições de estabilidade?
Empuxo, equilíbrio estático, tombamento e sobrecarga.
Deslizamento da base, tombamento, capacidade de carga e ruptura global.
Ruptura global, coeficiente de segurança, empuxo e capacidade de carga.
Cisalhamento, empuxo, tombamento e sobrecarga.
Empuxo ativo, empuxo passivo, deslizamento da base e equilíbrio estático.
Sabendo que um muro de arrimo feito em alvenaria de tijolos com seção retangular deve vencer uma altura de 5,5 metros, é correto afirmar que o dimensionamento do topo equivale a:
234 cm.
220 cm.
165 cm.
184 cm.
275 cm.
Nas análises pelo Método de Culmann, os taludes são considerados como finitos, sendo a altura crítica associada ao plano crítico do talude. O plano crítico de um talude possui a menor relação entre a tensão média de cisalhamento, que tende a provocar a ruptura, e a resistência ao cisalhamento do solo. Com base nessas informações, calcule a altura crítica para o talude indicado de acordo com o Método de Culmann, em metros.
O talude possui as seguintes propriedades: φ = 14°; β = 32°; γ = 1,6 tf/m³; c' = 1 tf/m².
Em caso de resposta decimal, considerar uma casa após a virgula.
24,5 m
26,3 m
22,8 m
29,3 m
19,4 m
Considerando os efeitos da sobrecarga, calcule a altura equivalente de uma camada de solo, em metros. O peso específico do solo é de 2 t/m³, e a pressão aplicada é de 3,0 t/m². Sabe-se que q = (γ.h).
2,5 m
2 m
1,5 m
1 m
6 m
O ensaio de palheta é também conhecido como vane test, em que é possível obter a resistência não drenada da argila (Su), e é obtido admitindo-se que a ruptura se dá na superfície do cilindro, onde o torque necessário para causar a ruptura é medido. Realizado esse ensaio em um solo onde foram obtidas as informações apresentadas a seguir, determine a coesão do material (Su), em kg/cm². Dados: D = 6,6 cm; H = 11 cm; M = 645 kg.cm. Em caso de resposta decimal, considere duas casas após a vírgula.
Considere a fórmula indicada a seguir:
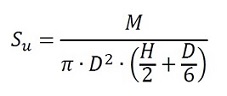
0,52 kg/cm²
0,95 kg/cm²
1,04 kg/cm²
0,39 kg/cm²
0,71 kg/cm²
Como o solo é um sistema particulado composto de partículas sólidas e espaços vazios, os quais podem estar parcial ou totalmente preenchidos com água, podemos afirmar que estão corretas apenas as afirmativas:
I. Uma das causas do decréscimo de volume é a compressão das partículas sólidas.
II. As deformações que ocorrem na água e nos grãos sólidos são desprezadas (pois são incompressíveis), calculando-se, portanto, apenas as deformações volumétricas do solo a partir da variação do índice de vazios.
III. As deformações ocorridas sempre serão uniformes, o que acarreta diretamente danos às estruturas assentes sobre o solo de fundação, o que inviabiliza a sua utilização.
Todas estão incorretas.
I e III.
II e III.
Todas estão corretas.
I e II.
Uma camada de argila saturada com 6,0 m de espessura, drenada por ambas as faces, apresenta as seguintes características: índice de vazios inicial igual a 1,02 e índice de compressão igual a 0,23. Determine o recalque primário da camada de argila, admitindo-se que essa sofra um acréscimo de tensões de 0,5 kg/cm².
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).

Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?
Empuxo, equilíbrio estático, tombamento e sobrecarga.
Deslizamento da base, tombamento, capacidade de carga e ruptura global.
Ruptura global, coeficiente de segurança, empuxo e capacidade de carga.
Cisalhamento, empuxo, tombamento e sobrecarga.
Empuxo ativo, empuxo passivo, deslizamento da base e equilíbrio estático.
Sabendo que um muro de arrimo feito em alvenaria de tijolos com seção retangular deve vencer uma altura de 5,5 metros, é correto afirmar que o dimensionamento do topo equivale a:
234 cm.
220 cm.
165 cm.
184 cm.
275 cm.
Nas análises pelo Método de Culmann, os taludes são considerados como finitos, sendo a altura crítica associada ao plano crítico do talude. O plano crítico de um talude possui a menor relação entre a tensão média de cisalhamento, que tende a provocar a ruptura, e a resistência ao cisalhamento do solo. Com base nessas informações, calcule a altura crítica para o talude indicado de acordo com o Método de Culmann, em metros.
O talude possui as seguintes propriedades: φ = 14°; β = 32°; γ = 1,6 tf/m³; c' = 1 tf/m².
Em caso de resposta decimal, considerar uma casa após a virgula.
24,5 m
26,3 m
22,8 m
29,3 m
19,4 m
Considerando os efeitos da sobrecarga, calcule a altura equivalente de uma camada de solo, em metros. O peso específico do solo é de 2 t/m³, e a pressão aplicada é de 3,0 t/m². Sabe-se que q = (γ.h).
2,5 m
2 m
1,5 m
1 m
6 m
O ensaio de palheta é também conhecido como vane test, em que é possível obter a resistência não drenada da argila (Su), e é obtido admitindo-se que a ruptura se dá na superfície do cilindro, onde o torque necessário para causar a ruptura é medido. Realizado esse ensaio em um solo onde foram obtidas as informações apresentadas a seguir, determine a coesão do material (Su), em kg/cm². Dados: D = 6,6 cm; H = 11 cm; M = 645 kg.cm. Em caso de resposta decimal, considere duas casas após a vírgula.
Considere a fórmula indicada a seguir:
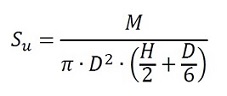
0,52 kg/cm²
0,95 kg/cm²
1,04 kg/cm²
0,39 kg/cm²
0,71 kg/cm²
Como o solo é um sistema particulado composto de partículas sólidas e espaços vazios, os quais podem estar parcial ou totalmente preenchidos com água, podemos afirmar que estão corretas apenas as afirmativas:
I. Uma das causas do decréscimo de volume é a compressão das partículas sólidas.
II. As deformações que ocorrem na água e nos grãos sólidos são desprezadas (pois são incompressíveis), calculando-se, portanto, apenas as deformações volumétricas do solo a partir da variação do índice de vazios.
III. As deformações ocorridas sempre serão uniformes, o que acarreta diretamente danos às estruturas assentes sobre o solo de fundação, o que inviabiliza a sua utilização.
Todas estão incorretas.
I e III.
II e III.
Todas estão corretas.
I e II.
Uma camada de argila saturada com 6,0 m de espessura, drenada por ambas as faces, apresenta as seguintes características: índice de vazios inicial igual a 1,02 e índice de compressão igual a 0,23. Determine o recalque primário da camada de argila, admitindo-se que essa sofra um acréscimo de tensões de 0,5 kg/cm².
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).

Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?
234 cm.
220 cm.
165 cm.
184 cm.
275 cm.
Nas análises pelo Método de Culmann, os taludes são considerados como finitos, sendo a altura crítica associada ao plano crítico do talude. O plano crítico de um talude possui a menor relação entre a tensão média de cisalhamento, que tende a provocar a ruptura, e a resistência ao cisalhamento do solo. Com base nessas informações, calcule a altura crítica para o talude indicado de acordo com o Método de Culmann, em metros.
O talude possui as seguintes propriedades: φ = 14°; β = 32°; γ = 1,6 tf/m³; c' = 1 tf/m².
Em caso de resposta decimal, considerar uma casa após a virgula.
24,5 m
26,3 m
22,8 m
29,3 m
19,4 m
Considerando os efeitos da sobrecarga, calcule a altura equivalente de uma camada de solo, em metros. O peso específico do solo é de 2 t/m³, e a pressão aplicada é de 3,0 t/m². Sabe-se que q = (γ.h).
2,5 m
2 m
1,5 m
1 m
6 m
O ensaio de palheta é também conhecido como vane test, em que é possível obter a resistência não drenada da argila (Su), e é obtido admitindo-se que a ruptura se dá na superfície do cilindro, onde o torque necessário para causar a ruptura é medido. Realizado esse ensaio em um solo onde foram obtidas as informações apresentadas a seguir, determine a coesão do material (Su), em kg/cm². Dados: D = 6,6 cm; H = 11 cm; M = 645 kg.cm. Em caso de resposta decimal, considere duas casas após a vírgula.
Considere a fórmula indicada a seguir:
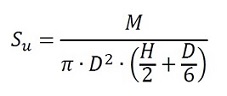
0,52 kg/cm²
0,95 kg/cm²
1,04 kg/cm²
0,39 kg/cm²
0,71 kg/cm²
Como o solo é um sistema particulado composto de partículas sólidas e espaços vazios, os quais podem estar parcial ou totalmente preenchidos com água, podemos afirmar que estão corretas apenas as afirmativas:
I. Uma das causas do decréscimo de volume é a compressão das partículas sólidas.
II. As deformações que ocorrem na água e nos grãos sólidos são desprezadas (pois são incompressíveis), calculando-se, portanto, apenas as deformações volumétricas do solo a partir da variação do índice de vazios.
III. As deformações ocorridas sempre serão uniformes, o que acarreta diretamente danos às estruturas assentes sobre o solo de fundação, o que inviabiliza a sua utilização.
Todas estão incorretas.
I e III.
II e III.
Todas estão corretas.
I e II.
Uma camada de argila saturada com 6,0 m de espessura, drenada por ambas as faces, apresenta as seguintes características: índice de vazios inicial igual a 1,02 e índice de compressão igual a 0,23. Determine o recalque primário da camada de argila, admitindo-se que essa sofra um acréscimo de tensões de 0,5 kg/cm².
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).

Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?
O talude possui as seguintes propriedades: φ = 14°; β = 32°; γ = 1,6 tf/m³; c' = 1 tf/m².
Em caso de resposta decimal, considerar uma casa após a virgula.
24,5 m
26,3 m
22,8 m
29,3 m
19,4 m
Considerando os efeitos da sobrecarga, calcule a altura equivalente de uma camada de solo, em metros. O peso específico do solo é de 2 t/m³, e a pressão aplicada é de 3,0 t/m². Sabe-se que q = (γ.h).
2,5 m
2 m
1,5 m
1 m
6 m
O ensaio de palheta é também conhecido como vane test, em que é possível obter a resistência não drenada da argila (Su), e é obtido admitindo-se que a ruptura se dá na superfície do cilindro, onde o torque necessário para causar a ruptura é medido. Realizado esse ensaio em um solo onde foram obtidas as informações apresentadas a seguir, determine a coesão do material (Su), em kg/cm². Dados: D = 6,6 cm; H = 11 cm; M = 645 kg.cm. Em caso de resposta decimal, considere duas casas após a vírgula.
Considere a fórmula indicada a seguir:
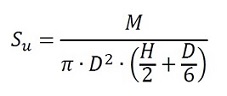
0,52 kg/cm²
0,95 kg/cm²
1,04 kg/cm²
0,39 kg/cm²
0,71 kg/cm²
Como o solo é um sistema particulado composto de partículas sólidas e espaços vazios, os quais podem estar parcial ou totalmente preenchidos com água, podemos afirmar que estão corretas apenas as afirmativas:
I. Uma das causas do decréscimo de volume é a compressão das partículas sólidas.
II. As deformações que ocorrem na água e nos grãos sólidos são desprezadas (pois são incompressíveis), calculando-se, portanto, apenas as deformações volumétricas do solo a partir da variação do índice de vazios.
III. As deformações ocorridas sempre serão uniformes, o que acarreta diretamente danos às estruturas assentes sobre o solo de fundação, o que inviabiliza a sua utilização.
Todas estão incorretas.
I e III.
II e III.
Todas estão corretas.
I e II.
Uma camada de argila saturada com 6,0 m de espessura, drenada por ambas as faces, apresenta as seguintes características: índice de vazios inicial igual a 1,02 e índice de compressão igual a 0,23. Determine o recalque primário da camada de argila, admitindo-se que essa sofra um acréscimo de tensões de 0,5 kg/cm².
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).

Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?
2,5 m
2 m
1,5 m
1 m
6 m
O ensaio de palheta é também conhecido como vane test, em que é possível obter a resistência não drenada da argila (Su), e é obtido admitindo-se que a ruptura se dá na superfície do cilindro, onde o torque necessário para causar a ruptura é medido. Realizado esse ensaio em um solo onde foram obtidas as informações apresentadas a seguir, determine a coesão do material (Su), em kg/cm². Dados: D = 6,6 cm; H = 11 cm; M = 645 kg.cm. Em caso de resposta decimal, considere duas casas após a vírgula.
Considere a fórmula indicada a seguir:
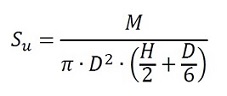
0,52 kg/cm²
0,95 kg/cm²
1,04 kg/cm²
0,39 kg/cm²
0,71 kg/cm²
Como o solo é um sistema particulado composto de partículas sólidas e espaços vazios, os quais podem estar parcial ou totalmente preenchidos com água, podemos afirmar que estão corretas apenas as afirmativas:
I. Uma das causas do decréscimo de volume é a compressão das partículas sólidas.
II. As deformações que ocorrem na água e nos grãos sólidos são desprezadas (pois são incompressíveis), calculando-se, portanto, apenas as deformações volumétricas do solo a partir da variação do índice de vazios.
III. As deformações ocorridas sempre serão uniformes, o que acarreta diretamente danos às estruturas assentes sobre o solo de fundação, o que inviabiliza a sua utilização.
Todas estão incorretas.
I e III.
II e III.
Todas estão corretas.
I e II.
Uma camada de argila saturada com 6,0 m de espessura, drenada por ambas as faces, apresenta as seguintes características: índice de vazios inicial igual a 1,02 e índice de compressão igual a 0,23. Determine o recalque primário da camada de argila, admitindo-se que essa sofra um acréscimo de tensões de 0,5 kg/cm².
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).

Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?
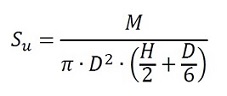
0,52 kg/cm²
0,95 kg/cm²
1,04 kg/cm²
0,39 kg/cm²
0,71 kg/cm²
Como o solo é um sistema particulado composto de partículas sólidas e espaços vazios, os quais podem estar parcial ou totalmente preenchidos com água, podemos afirmar que estão corretas apenas as afirmativas:
I. Uma das causas do decréscimo de volume é a compressão das partículas sólidas.
II. As deformações que ocorrem na água e nos grãos sólidos são desprezadas (pois são incompressíveis), calculando-se, portanto, apenas as deformações volumétricas do solo a partir da variação do índice de vazios.
III. As deformações ocorridas sempre serão uniformes, o que acarreta diretamente danos às estruturas assentes sobre o solo de fundação, o que inviabiliza a sua utilização.
Todas estão incorretas.
I e III.
II e III.
Todas estão corretas.
I e II.
Uma camada de argila saturada com 6,0 m de espessura, drenada por ambas as faces, apresenta as seguintes características: índice de vazios inicial igual a 1,02 e índice de compressão igual a 0,23. Determine o recalque primário da camada de argila, admitindo-se que essa sofra um acréscimo de tensões de 0,5 kg/cm².
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).

Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?
I. Uma das causas do decréscimo de volume é a compressão das partículas sólidas.
II. As deformações que ocorrem na água e nos grãos sólidos são desprezadas (pois são incompressíveis), calculando-se, portanto, apenas as deformações volumétricas do solo a partir da variação do índice de vazios.
III. As deformações ocorridas sempre serão uniformes, o que acarreta diretamente danos às estruturas assentes sobre o solo de fundação, o que inviabiliza a sua utilização.
Todas estão incorretas.
I e III.
II e III.
Todas estão corretas.
I e II.
Uma camada de argila saturada com 6,0 m de espessura, drenada por ambas as faces, apresenta as seguintes características: índice de vazios inicial igual a 1,02 e índice de compressão igual a 0,23. Determine o recalque primário da camada de argila, admitindo-se que essa sofra um acréscimo de tensões de 0,5 kg/cm².
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).

Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?
1,82 cm.
95,30 cm.
20,57 cm.
9,53 cm.
68,32 cm.
Uma solução plausível para drenar pequenas bacias, devido às chuvas de grande intensidade, é o uso de barragens. A altura da crista da barragem é igual à soma da altura da lâmina de água normal (Hn) com a altura da lâmina de água do ladrão (H1), acrescida da folga (F), como ilustrado na figura a seguir. O valor de H1 pode ser assumido igual a 1,0 m e recomenda-se que F corresponda a, no mínimo, 0,5 m.
O gráfico abaixo apresenta o volume acumulado para as cotas da bacia em m³ (x106).

Fonte: Adaptado de ENADE (2011).
Qual o valor da cota da barragem (H = Hn + H1 + f), aproximadamente, para um volume máximo de cheia de 80 x 106 m³?
