MECÂNICA GERAL
Duas forças são aplicadas ao olhal a fim de remover a estaca mostrada. Determine o ângulo θ e o valor da força F de modo que a força resultante seja orientada verticalmente para cima no eixo y e tenha uma intensidade de 1 kN.
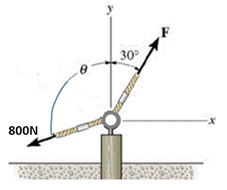
65,64° e 1487,43 N
65,64° e 1240,43 N
111,62° e 982,4 N
83,45° e 982,4 N
111,32° e 1490,50 N
Qual o esforço cortante e o momento em C da viga abaixo.
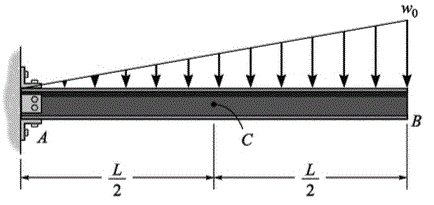
Vc = 4.wo L/5
Mc = -6.wo L² /36
Vc = 3.wo L/8
Mc = -5.wo L² /48
Vc = 4.wo L²/6
Mc = -3.wo L /36
Vc = 5.wo L/8
Mc = -2.wo L² /48
Vc = 5.wo L³/8
Mc = -9.wo L² /36
Qual o esforço cortante e momento no ponto C:
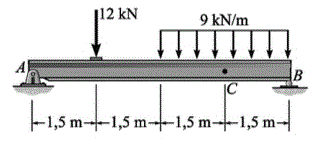
VC =-9,75 kN
MC =24,75 kN.m
VC =-7,75 kN
MC =22,75 kN.m
VC =6,75 kN
MC =-14,75 kN.m
VC =-8,75 kN
MC =26,75 kN.m
VC =8,75 kN
MC =-20,75 kN.m
Determine o momento da força em relação ao ponto O.
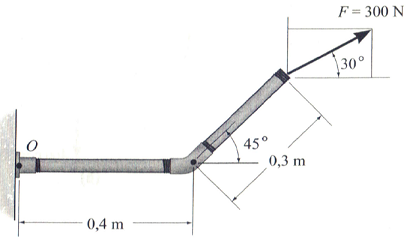
30,4 N.m
36,7 N.m
21,5 N.m
46,6 N.m
32,5 N.m
A placa circular é parcialmente suportada pelo cabo AB. Sabe-se que a força no cabo em A é igual a 1 kN, essa força na forma de um vetor cartesiano é:
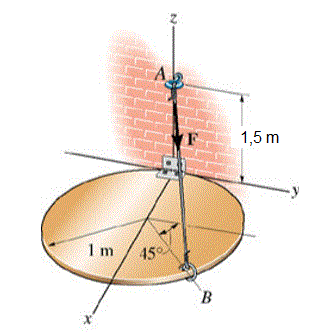
F= {- 321 i + 245 j + 629 k} N
F= {654 i + 147 j + 220 k} N
F= {156 i - 456 j - 630 k} N
F= {0 i +357 j + 630 k} N
F= {717 i + 297 j - 630 k} N
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):
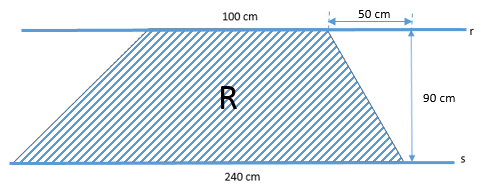
O centroide CG da região R é dado por:
(128,63 ; 36,28)
(124,63 ; 38,28)
(128,36 ; 38,82)
(124,63 ; 38,82)
(128,63 ; 38,82)
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:
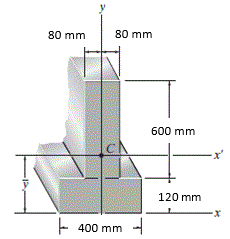
2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,624 . 10 8 mm 4
Considerando a treliça dada a seguir,
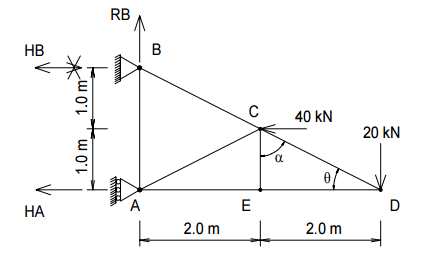
Determinando a força FCD e analisando se é tração ou compressão, podemos admitir que
FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
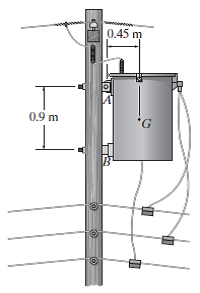
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.
Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
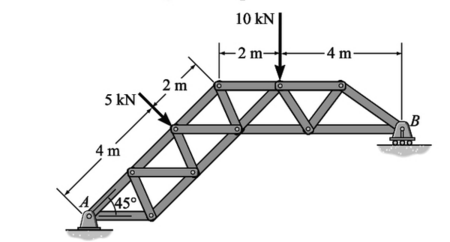
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.

65,64° e 1487,43 N
65,64° e 1240,43 N
111,62° e 982,4 N
83,45° e 982,4 N
111,32° e 1490,50 N
Qual o esforço cortante e o momento em C da viga abaixo.

Vc = 4.wo L/5
Mc = -6.wo L² /36
Vc = 3.wo L/8
Mc = -5.wo L² /48
Vc = 4.wo L²/6
Mc = -3.wo L /36
Vc = 5.wo L/8
Mc = -2.wo L² /48
Vc = 5.wo L³/8
Mc = -9.wo L² /36
Qual o esforço cortante e momento no ponto C:

VC =-9,75 kN
MC =24,75 kN.m
VC =-7,75 kN
MC =22,75 kN.m
VC =6,75 kN
MC =-14,75 kN.m
VC =-8,75 kN
MC =26,75 kN.m
VC =8,75 kN
MC =-20,75 kN.m
Determine o momento da força em relação ao ponto O.

30,4 N.m
36,7 N.m
21,5 N.m
46,6 N.m
32,5 N.m
A placa circular é parcialmente suportada pelo cabo AB. Sabe-se que a força no cabo em A é igual a 1 kN, essa força na forma de um vetor cartesiano é:

F= {- 321 i + 245 j + 629 k} N
F= {654 i + 147 j + 220 k} N
F= {156 i - 456 j - 630 k} N
F= {0 i +357 j + 630 k} N
F= {717 i + 297 j - 630 k} N
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,63 ; 36,28)
(124,63 ; 38,28)
(128,36 ; 38,82)
(124,63 ; 38,82)
(128,63 ; 38,82)
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:

2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,624 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando a força FCD e analisando se é tração ou compressão, podemos admitir que
FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.

Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.


Vc = 4.wo L/5
Mc = -6.wo L² /36
Vc = 3.wo L/8
Mc = -5.wo L² /48
Vc = 4.wo L²/6
Mc = -3.wo L /36
Vc = 5.wo L/8
Mc = -2.wo L² /48
Vc = 5.wo L³/8
Mc = -9.wo L² /36
Qual o esforço cortante e momento no ponto C:

VC =-9,75 kN
MC =24,75 kN.m
VC =-7,75 kN
MC =22,75 kN.m
VC =6,75 kN
MC =-14,75 kN.m
VC =-8,75 kN
MC =26,75 kN.m
VC =8,75 kN
MC =-20,75 kN.m
Determine o momento da força em relação ao ponto O.

30,4 N.m
36,7 N.m
21,5 N.m
46,6 N.m
32,5 N.m
A placa circular é parcialmente suportada pelo cabo AB. Sabe-se que a força no cabo em A é igual a 1 kN, essa força na forma de um vetor cartesiano é:

F= {- 321 i + 245 j + 629 k} N
F= {654 i + 147 j + 220 k} N
F= {156 i - 456 j - 630 k} N
F= {0 i +357 j + 630 k} N
F= {717 i + 297 j - 630 k} N
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,63 ; 36,28)
(124,63 ; 38,28)
(128,36 ; 38,82)
(124,63 ; 38,82)
(128,63 ; 38,82)
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:

2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,624 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando a força FCD e analisando se é tração ou compressão, podemos admitir que
FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.

Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.


VC =-9,75 kN
MC =24,75 kN.m
VC =-7,75 kN
MC =22,75 kN.m
VC =6,75 kN
MC =-14,75 kN.m
VC =-8,75 kN
MC =26,75 kN.m
VC =8,75 kN
MC =-20,75 kN.m
Determine o momento da força em relação ao ponto O.

30,4 N.m
36,7 N.m
21,5 N.m
46,6 N.m
32,5 N.m
A placa circular é parcialmente suportada pelo cabo AB. Sabe-se que a força no cabo em A é igual a 1 kN, essa força na forma de um vetor cartesiano é:

F= {- 321 i + 245 j + 629 k} N
F= {654 i + 147 j + 220 k} N
F= {156 i - 456 j - 630 k} N
F= {0 i +357 j + 630 k} N
F= {717 i + 297 j - 630 k} N
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,63 ; 36,28)
(124,63 ; 38,28)
(128,36 ; 38,82)
(124,63 ; 38,82)
(128,63 ; 38,82)
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:

2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,624 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando a força FCD e analisando se é tração ou compressão, podemos admitir que
FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.

Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.

30,4 N.m
36,7 N.m
21,5 N.m
46,6 N.m
32,5 N.m
A placa circular é parcialmente suportada pelo cabo AB. Sabe-se que a força no cabo em A é igual a 1 kN, essa força na forma de um vetor cartesiano é:

F= {- 321 i + 245 j + 629 k} N
F= {654 i + 147 j + 220 k} N
F= {156 i - 456 j - 630 k} N
F= {0 i +357 j + 630 k} N
F= {717 i + 297 j - 630 k} N
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,63 ; 36,28)
(124,63 ; 38,28)
(128,36 ; 38,82)
(124,63 ; 38,82)
(128,63 ; 38,82)
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:

2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,624 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando a força FCD e analisando se é tração ou compressão, podemos admitir que
FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.

Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.


F= {- 321 i + 245 j + 629 k} N
F= {654 i + 147 j + 220 k} N
F= {156 i - 456 j - 630 k} N
F= {0 i +357 j + 630 k} N
F= {717 i + 297 j - 630 k} N
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,63 ; 36,28)
(124,63 ; 38,28)
(128,36 ; 38,82)
(124,63 ; 38,82)
(128,63 ; 38,82)
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:

2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,624 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando a força FCD e analisando se é tração ou compressão, podemos admitir que
FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.

Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.


(128,63 ; 36,28)
(124,63 ; 38,28)
(128,36 ; 38,82)
(124,63 ; 38,82)
(128,63 ; 38,82)
O momento de inércia da área de seção transversal da viga em relação ao eixo Y é APROXIMADAMENTE:

2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,624 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando a força FCD e analisando se é tração ou compressão, podemos admitir que
FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.

Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.


2,937 . 10 8 mm 4
8,448 . 10 8 mm 4
7,924 . 10 8 mm 4
5,624 . 10 8 mm 4
2,624 . 10 8 mm 4
Considerando a treliça dada a seguir,

Determinando a força FCD e analisando se é tração ou compressão, podemos admitir que
FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.

Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.


FCD = - 22,4 kN, Compressão.
FCD = - 44,7 kN, Compressão.
FCD = 44,7 kN, Tração.
FCD = 40 kN, Tração.
FCD = - 40 kN, Compressão.
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.

Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N
A treliça é suportada por um pino em A e um rolete em B. Determine as reações de apoio em B, se houverem.


Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 850 N
Ay= 150 N
NB= 650 N