MECÂNICA GERAL
Com base na figura ilustrada abaixo, assinale a alternativa correta que apresenta a localização do centro de gravidade (centroide).
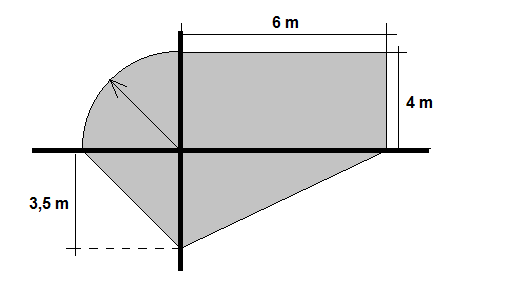
O CG da figura acima é dado por:
(1,15 ; 0,9 )
(1,35 ; 0,9 )
(1,25 ; 0,7 )
(1,25 ; 0,9 )
(1,05 ; 0,9 )
Pelo método de integrais, usando área diferencial. determine a centroide na figura abaixo.
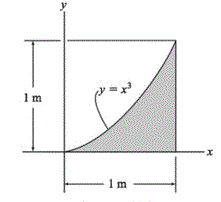
X = 1,1 m e Y= 0,45 m
X = 0,8 m e Y= 0,286 m
X = 0,35 m e Y= 0,6 m
X = 0,65 m e Y= 0,26 m
X = 0,9 m e Y= 0,63 m
Considerando a treliça dada a seguir,
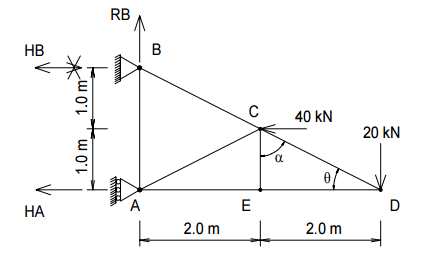
Determinando HA e HB , podemos admitir que
HB = 2HA .
HA = 3HB .
3HB = 2HA .
HA = HB .
HA = -3HB .
O protótipo de uma passagem elevada com as suas respectivas medidas estão na figura abaixo. Assinale a alternativa correta que apresenta o momento de inércia da área da seção transversal em relação ao eixo x.

254.104 mm4
205.104 mm4
155.104 mm4
301.104 mm4
288.104 mm4
Duas lanchas rebocam um barco de passageiros que se encontra com problemas em seus motores. Sabendo-se que a força resultante é igual a 50kN, encontre suas componentes nas direções AC e BC.
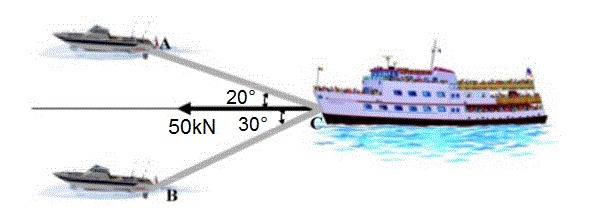
AC = 32, 63 kN
BC = 22,32 kN
AC = 34,35 kN
BC = 28,73 kN
AC = 25 kN
BC = 35 kN
AC = 22, 65 kN
BC = 42,11 kN
AC = 30 kN
BC = 30 kN
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:
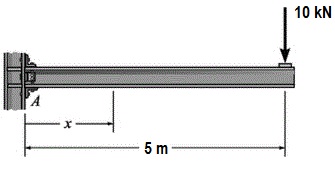
V = 10 ; M = 10x - 50
V = 10x ; M = x - 50
V = 10 ; M = x2 - 50
V = 50 ; M = 10x - 50
V = 10x ; M = 10x - 50
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 150 N, determine a intensidade da força FA que o garoto em A precisa exercer para impedir que o portão não gire. Despreze a espessura do portão.
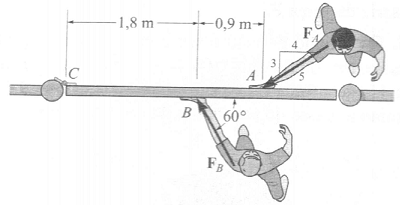
144,3 N
342 N
90,5 N
234,5 N
234,2 N
Determine o momento resultante produzido pelas forças em relação ao ponto O.
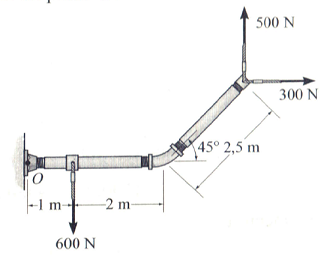
0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.
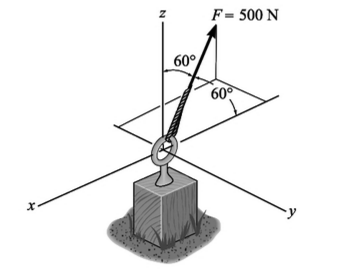
{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
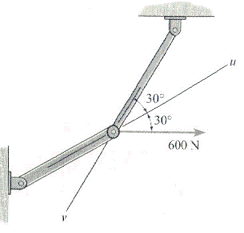
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.

(1,15 ; 0,9 )
(1,35 ; 0,9 )
(1,25 ; 0,7 )
(1,25 ; 0,9 )
(1,05 ; 0,9 )
Pelo método de integrais, usando área diferencial. determine a centroide na figura abaixo.

X = 1,1 m e Y= 0,45 m
X = 0,8 m e Y= 0,286 m
X = 0,35 m e Y= 0,6 m
X = 0,65 m e Y= 0,26 m
X = 0,9 m e Y= 0,63 m
Considerando a treliça dada a seguir,

Determinando HA e HB , podemos admitir que
HB = 2HA .
HA = 3HB .
3HB = 2HA .
HA = HB .
HA = -3HB .
O protótipo de uma passagem elevada com as suas respectivas medidas estão na figura abaixo. Assinale a alternativa correta que apresenta o momento de inércia da área da seção transversal em relação ao eixo x.

254.104 mm4
205.104 mm4
155.104 mm4
301.104 mm4
288.104 mm4
Duas lanchas rebocam um barco de passageiros que se encontra com problemas em seus motores. Sabendo-se que a força resultante é igual a 50kN, encontre suas componentes nas direções AC e BC.

AC = 32, 63 kN
BC = 22,32 kN
AC = 34,35 kN
BC = 28,73 kN
AC = 25 kN
BC = 35 kN
AC = 22, 65 kN
BC = 42,11 kN
AC = 30 kN
BC = 30 kN
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:

V = 10 ; M = 10x - 50
V = 10x ; M = x - 50
V = 10 ; M = x2 - 50
V = 50 ; M = 10x - 50
V = 10x ; M = 10x - 50
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 150 N, determine a intensidade da força FA que o garoto em A precisa exercer para impedir que o portão não gire. Despreze a espessura do portão.

144,3 N
342 N
90,5 N
234,5 N
234,2 N
Determine o momento resultante produzido pelas forças em relação ao ponto O.

0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.

{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.


X = 1,1 m e Y= 0,45 m
X = 0,8 m e Y= 0,286 m
X = 0,35 m e Y= 0,6 m
X = 0,65 m e Y= 0,26 m
X = 0,9 m e Y= 0,63 m
Considerando a treliça dada a seguir,

Determinando HA e HB , podemos admitir que
HB = 2HA .
HA = 3HB .
3HB = 2HA .
HA = HB .
HA = -3HB .
O protótipo de uma passagem elevada com as suas respectivas medidas estão na figura abaixo. Assinale a alternativa correta que apresenta o momento de inércia da área da seção transversal em relação ao eixo x.

254.104 mm4
205.104 mm4
155.104 mm4
301.104 mm4
288.104 mm4
Duas lanchas rebocam um barco de passageiros que se encontra com problemas em seus motores. Sabendo-se que a força resultante é igual a 50kN, encontre suas componentes nas direções AC e BC.

AC = 32, 63 kN
BC = 22,32 kN
AC = 34,35 kN
BC = 28,73 kN
AC = 25 kN
BC = 35 kN
AC = 22, 65 kN
BC = 42,11 kN
AC = 30 kN
BC = 30 kN
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:

V = 10 ; M = 10x - 50
V = 10x ; M = x - 50
V = 10 ; M = x2 - 50
V = 50 ; M = 10x - 50
V = 10x ; M = 10x - 50
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 150 N, determine a intensidade da força FA que o garoto em A precisa exercer para impedir que o portão não gire. Despreze a espessura do portão.

144,3 N
342 N
90,5 N
234,5 N
234,2 N
Determine o momento resultante produzido pelas forças em relação ao ponto O.

0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.

{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.


HB = 2HA .
HA = 3HB .
3HB = 2HA .
HA = HB .
HA = -3HB .
O protótipo de uma passagem elevada com as suas respectivas medidas estão na figura abaixo. Assinale a alternativa correta que apresenta o momento de inércia da área da seção transversal em relação ao eixo x.

254.104 mm4
205.104 mm4
155.104 mm4
301.104 mm4
288.104 mm4
Duas lanchas rebocam um barco de passageiros que se encontra com problemas em seus motores. Sabendo-se que a força resultante é igual a 50kN, encontre suas componentes nas direções AC e BC.

AC = 32, 63 kN
BC = 22,32 kN
AC = 34,35 kN
BC = 28,73 kN
AC = 25 kN
BC = 35 kN
AC = 22, 65 kN
BC = 42,11 kN
AC = 30 kN
BC = 30 kN
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:

V = 10 ; M = 10x - 50
V = 10x ; M = x - 50
V = 10 ; M = x2 - 50
V = 50 ; M = 10x - 50
V = 10x ; M = 10x - 50
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 150 N, determine a intensidade da força FA que o garoto em A precisa exercer para impedir que o portão não gire. Despreze a espessura do portão.

144,3 N
342 N
90,5 N
234,5 N
234,2 N
Determine o momento resultante produzido pelas forças em relação ao ponto O.

0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.

{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.

254.104 mm4
205.104 mm4
155.104 mm4
301.104 mm4
288.104 mm4
Duas lanchas rebocam um barco de passageiros que se encontra com problemas em seus motores. Sabendo-se que a força resultante é igual a 50kN, encontre suas componentes nas direções AC e BC.

AC = 32, 63 kN
BC = 22,32 kN
AC = 34,35 kN
BC = 28,73 kN
AC = 25 kN
BC = 35 kN
AC = 22, 65 kN
BC = 42,11 kN
AC = 30 kN
BC = 30 kN
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:

V = 10 ; M = 10x - 50
V = 10x ; M = x - 50
V = 10 ; M = x2 - 50
V = 50 ; M = 10x - 50
V = 10x ; M = 10x - 50
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 150 N, determine a intensidade da força FA que o garoto em A precisa exercer para impedir que o portão não gire. Despreze a espessura do portão.

144,3 N
342 N
90,5 N
234,5 N
234,2 N
Determine o momento resultante produzido pelas forças em relação ao ponto O.

0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.

{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.


AC = 32, 63 kN
BC = 22,32 kN
AC = 34,35 kN
BC = 28,73 kN
AC = 25 kN
BC = 35 kN
AC = 22, 65 kN
BC = 42,11 kN
AC = 30 kN
BC = 30 kN
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:

V = 10 ; M = 10x - 50
V = 10x ; M = x - 50
V = 10 ; M = x2 - 50
V = 50 ; M = 10x - 50
V = 10x ; M = 10x - 50
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 150 N, determine a intensidade da força FA que o garoto em A precisa exercer para impedir que o portão não gire. Despreze a espessura do portão.

144,3 N
342 N
90,5 N
234,5 N
234,2 N
Determine o momento resultante produzido pelas forças em relação ao ponto O.

0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.

{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.


V = 10 ; M = 10x - 50
V = 10x ; M = x - 50
V = 10 ; M = x2 - 50
V = 50 ; M = 10x - 50
V = 10x ; M = 10x - 50
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 150 N, determine a intensidade da força FA que o garoto em A precisa exercer para impedir que o portão não gire. Despreze a espessura do portão.

144,3 N
342 N
90,5 N
234,5 N
234,2 N
Determine o momento resultante produzido pelas forças em relação ao ponto O.

0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.

{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.


144,3 N
342 N
90,5 N
234,5 N
234,2 N
Determine o momento resultante produzido pelas forças em relação ao ponto O.

0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.

{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.


0,98 KN.m
2,15 KN.m
2,5 KN.m
2,23 KN.m
1,25 KN.m
Expresse a força como um vetor cartesiano.

{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.


{354i -354j +250k} N
{180i -250j +250k} N
{-250i -354j +250k} N
{354i -250j +250k} N
{ 250i -354j -250k} N
Decomponha a força horizontal de 600 N do esquema abaixo nos componentes que atuam ao longo dos eixos u e v e determine as intensidades desses componentes.

