MECÂNICA GERAL
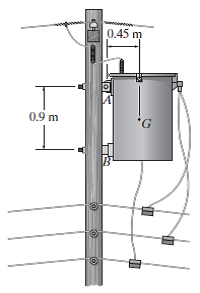
O transformador elétrico de 1500 N com centro de gravidade em G é sustentado por um pino em A e uma sapata lisa em B. Determine as componentes horizontal e vertical da reação no pino A e a reação da sapata B sobre o transformador.
Ax= 850 N
Ay= 150 N
NB= 650 N
Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
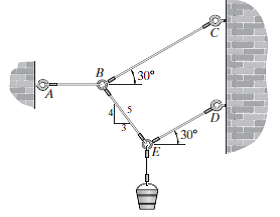
Determine o peso máximo do balde (W) que o sistema de fios pode suportar, de modo que nenhum fio desenvolva uma tração maior que 0,5 kN.
Dica: Começar pelas equações de equilíbrio em E, para achar TBE.
(W =0,138 kN)
W = 0,478 kN
W = 0,289 kN
W = 0,401 kN
W = 0,379 kN
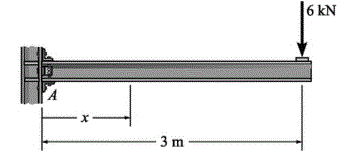
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:
V = 6+x
M = -3x+18
V = 6
M = 6x-18
V = 6-x
M = x²-12
V = 6x
M = 3x²
V = 2x
M = x²-6
Qual a força normal interna e o esforço cortante em C. Considere que C está à direita do momento binário dado.
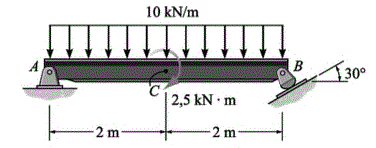
NC = -11,9 kN
VC = -0,62 kN
NC = 12,5 kN
VC = 1,22 kN
NC = -8,5 kN
VC = -0,54 kN
NC = -8,35 kN
VC = 2,25 kN
NC = -8,3 kN
VC = -1,25 kN
Os dois garotos empurram o portão com forças de FB = 250 N e FA = 150 N como mostrado. Determine o momento de cada força em relação a C. Em que sentido o portão girará, horário ou anti-horário? Despreze a espessura do portão.
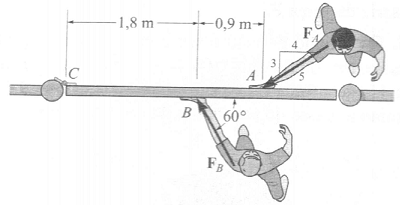
243 N.m, 389,7 N.m, o portão girará no sentido horário
243 N.m, 389,7 N.m, o portão girará no sentido anti-horário
245 N.m, 245 N.m, o portão não girará
127 N.m, 243,4 N.m, o portão girará no sentido horário
127 N.m, 243,4 N.m, o portão girará no sentido anti-horário
Determine o momento resultante produzido pelas forças em relação ao ponto O.
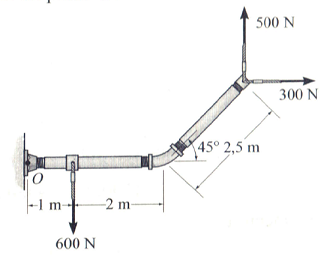
1,25 KN.m
2,15 KN.m
2,5 KN.m
0,98 KN.m
2,23 KN.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:
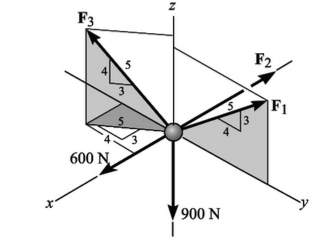
F2=F1<F3
F2<F3<F1
F1<F2<F3
F1<F3<F2
F2<F1<F3
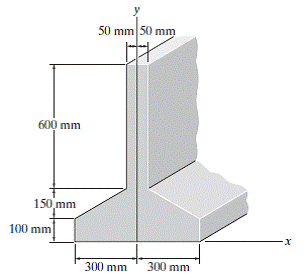
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):
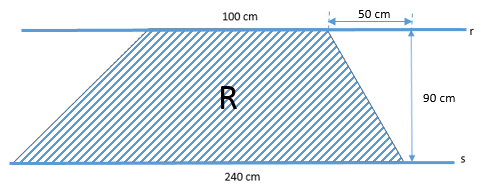
O centroide CG da região R é dado por:
(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).
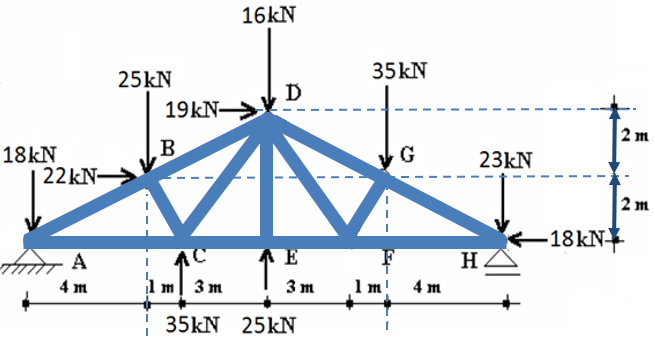

Ax= 850 N
Ay= 150 N
NB= 650 N
Ax= 1500 N
Ay= 1500 N
NB= 1500 N
Ax= 150 N
Ay= 750 N
NB= 250 N
Ax= 750 N
Ay= 1500 N
NB= 750 N
Ax= 800 N
Ay= 1600 N
NB= 750 N
Determine o peso máximo do balde (W) que o sistema de fios pode suportar, de modo que nenhum fio desenvolva uma tração maior que 0,5 kN.
Dica: Começar pelas equações de equilíbrio em E, para achar TBE.

(W =0,138 kN)
W = 0,478 kN
W = 0,289 kN
W = 0,401 kN
W = 0,379 kN
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:

V = 6+x
M = -3x+18
V = 6
M = 6x-18
V = 6-x
M = x²-12
V = 6x
M = 3x²
V = 2x
M = x²-6
Qual a força normal interna e o esforço cortante em C. Considere que C está à direita do momento binário dado.

NC = -11,9 kN
VC = -0,62 kN
NC = 12,5 kN
VC = 1,22 kN
NC = -8,5 kN
VC = -0,54 kN
NC = -8,35 kN
VC = 2,25 kN
NC = -8,3 kN
VC = -1,25 kN
Os dois garotos empurram o portão com forças de FB = 250 N e FA = 150 N como mostrado. Determine o momento de cada força em relação a C. Em que sentido o portão girará, horário ou anti-horário? Despreze a espessura do portão.

243 N.m, 389,7 N.m, o portão girará no sentido horário
243 N.m, 389,7 N.m, o portão girará no sentido anti-horário
245 N.m, 245 N.m, o portão não girará
127 N.m, 243,4 N.m, o portão girará no sentido horário
127 N.m, 243,4 N.m, o portão girará no sentido anti-horário
Determine o momento resultante produzido pelas forças em relação ao ponto O.

1,25 KN.m
2,15 KN.m
2,5 KN.m
0,98 KN.m
2,23 KN.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1<F3
F2<F3<F1
F1<F2<F3
F1<F3<F2
F2<F1<F3
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).


(W =0,138 kN)
W = 0,478 kN
W = 0,289 kN
W = 0,401 kN
W = 0,379 kN
Quais as funções em relação a x em relação ao momento fletor e esforço cortante da situação abaixo:

V = 6+x
M = -3x+18
V = 6
M = 6x-18
V = 6-x
M = x²-12
V = 6x
M = 3x²
V = 2x
M = x²-6
Qual a força normal interna e o esforço cortante em C. Considere que C está à direita do momento binário dado.

NC = -11,9 kN
VC = -0,62 kN
NC = 12,5 kN
VC = 1,22 kN
NC = -8,5 kN
VC = -0,54 kN
NC = -8,35 kN
VC = 2,25 kN
NC = -8,3 kN
VC = -1,25 kN
Os dois garotos empurram o portão com forças de FB = 250 N e FA = 150 N como mostrado. Determine o momento de cada força em relação a C. Em que sentido o portão girará, horário ou anti-horário? Despreze a espessura do portão.

243 N.m, 389,7 N.m, o portão girará no sentido horário
243 N.m, 389,7 N.m, o portão girará no sentido anti-horário
245 N.m, 245 N.m, o portão não girará
127 N.m, 243,4 N.m, o portão girará no sentido horário
127 N.m, 243,4 N.m, o portão girará no sentido anti-horário
Determine o momento resultante produzido pelas forças em relação ao ponto O.

1,25 KN.m
2,15 KN.m
2,5 KN.m
0,98 KN.m
2,23 KN.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1<F3
F2<F3<F1
F1<F2<F3
F1<F3<F2
F2<F1<F3
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).


V = 6+x
M = -3x+18
V = 6
M = 6x-18
V = 6-x
M = x²-12
V = 6x
M = 3x²
V = 2x
M = x²-6
Qual a força normal interna e o esforço cortante em C. Considere que C está à direita do momento binário dado.

NC = -11,9 kN
VC = -0,62 kN
NC = 12,5 kN
VC = 1,22 kN
NC = -8,5 kN
VC = -0,54 kN
NC = -8,35 kN
VC = 2,25 kN
NC = -8,3 kN
VC = -1,25 kN
Os dois garotos empurram o portão com forças de FB = 250 N e FA = 150 N como mostrado. Determine o momento de cada força em relação a C. Em que sentido o portão girará, horário ou anti-horário? Despreze a espessura do portão.

243 N.m, 389,7 N.m, o portão girará no sentido horário
243 N.m, 389,7 N.m, o portão girará no sentido anti-horário
245 N.m, 245 N.m, o portão não girará
127 N.m, 243,4 N.m, o portão girará no sentido horário
127 N.m, 243,4 N.m, o portão girará no sentido anti-horário
Determine o momento resultante produzido pelas forças em relação ao ponto O.

1,25 KN.m
2,15 KN.m
2,5 KN.m
0,98 KN.m
2,23 KN.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1<F3
F2<F3<F1
F1<F2<F3
F1<F3<F2
F2<F1<F3
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).


NC = -11,9 kN
VC = -0,62 kN
NC = 12,5 kN
VC = 1,22 kN
NC = -8,5 kN
VC = -0,54 kN
NC = -8,35 kN
VC = 2,25 kN
NC = -8,3 kN
VC = -1,25 kN
Os dois garotos empurram o portão com forças de FB = 250 N e FA = 150 N como mostrado. Determine o momento de cada força em relação a C. Em que sentido o portão girará, horário ou anti-horário? Despreze a espessura do portão.

243 N.m, 389,7 N.m, o portão girará no sentido horário
243 N.m, 389,7 N.m, o portão girará no sentido anti-horário
245 N.m, 245 N.m, o portão não girará
127 N.m, 243,4 N.m, o portão girará no sentido horário
127 N.m, 243,4 N.m, o portão girará no sentido anti-horário
Determine o momento resultante produzido pelas forças em relação ao ponto O.

1,25 KN.m
2,15 KN.m
2,5 KN.m
0,98 KN.m
2,23 KN.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1<F3
F2<F3<F1
F1<F2<F3
F1<F3<F2
F2<F1<F3
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).


243 N.m, 389,7 N.m, o portão girará no sentido horário
243 N.m, 389,7 N.m, o portão girará no sentido anti-horário
245 N.m, 245 N.m, o portão não girará
127 N.m, 243,4 N.m, o portão girará no sentido horário
127 N.m, 243,4 N.m, o portão girará no sentido anti-horário
Determine o momento resultante produzido pelas forças em relação ao ponto O.

1,25 KN.m
2,15 KN.m
2,5 KN.m
0,98 KN.m
2,23 KN.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1<F3
F2<F3<F1
F1<F2<F3
F1<F3<F2
F2<F1<F3
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).


1,25 KN.m
2,15 KN.m
2,5 KN.m
0,98 KN.m
2,23 KN.m
É correto afirmar em relação as intensidades das forças F1, F2 e F3, de modo que a partícula seja mantida em equilíbrio, que:

F2=F1<F3
F2<F3<F1
F1<F2<F3
F1<F3<F2
F2<F1<F3
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).


F2=F1<F3
F2<F3<F1
F1<F2<F3
F1<F3<F2
F2<F1<F3
Uma região R tem o formato de um trapézio ( r // s ) cuja base maior mede 240 cm e base menor 100 cm, conforme mostra a figura a seguir,( Considerar a origem dos eixos sendo o canto inferior esquerdo da figura):

O centroide CG da região R é dado por:
(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).


(128,36 ; 38,82)
(124,63 ; 38,82)
(124,63 ; 38,28)
(128,63 ; 36,28)
(128,63 ; 38,82)
Com base na treliça abaixo, determine a força na barra AB. Dado( RAy =9,44 KN).