MECÂNICA GERAL
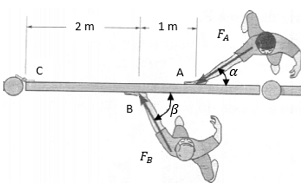
Dois garotos empurram o portão conforme mostrado. Se o garoto em B exerce uma força FB = 120 N, determine o valor aproximado da intensidade da força FA, que o garoto em A precisa exercer para que o portão não gire. Considere Alpha igual a 30° e Beta igual a 45°, despreze a espessura do portão.
189,45 N
200,55 N
113,14 N
148,87 N
138,56 N
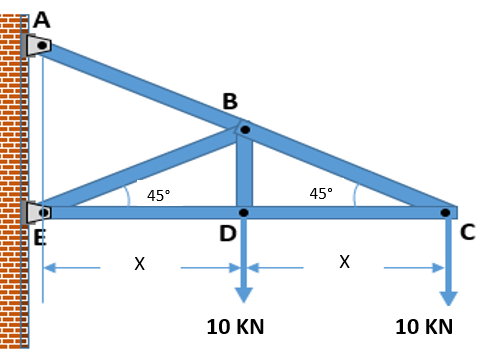
as forças normais FBC e FBD do esquema abaixo, são respectivamente:
14,14 KN e 10 KN
10 KN e - 13 KN
-14,14 KN e 13 KN
- 10 KN e 12 KN
-14,14 KN e - 10 KN
O cabo BD exerce no poste AC uma força P dirigida ao longo de BD. Se P tem uma componente de 150N perpendicular ao poste AC, então o valor da sua componente ao longo da linha AC será aproximadamente igual a
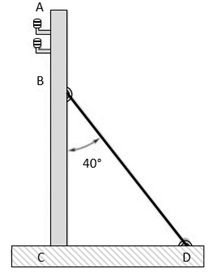
Dados: sen 40° = cos50° = 0,6428 e sen 50° = cos40° = 0,7661
195,82 N
178,75 N
189,45 N
213,50 N
199,57 N
Considere a figura a seguir,
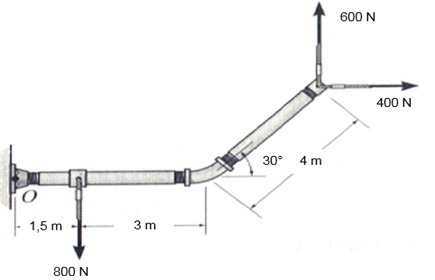
O momento resultante produzido pelas forças em relação ao ponto O é aproximadamente
2,44 KN
1,29 KN
2,25 KN
2,77 KN
1,38 KN
Duas forças atuam sobre o gancho mostrado na figura. Especifique os ângulos (α,β,γ) diretores coordenados aproximados de F2, de modo que a força resultante FR atue ao longo do eixo y positivo e tenha intensidade de 700 N.
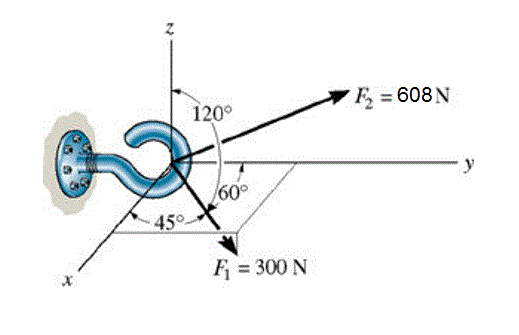
78°, 91° e 145°
63°, 163° e 123°
110°, 25° e 76°
46°, 28° e 34°
92°, 27° e 124°
A estrutura mostrada na figura está submetida a uma força horizontal. Determine a intensidade aproximada dos componentes dessa força, paralela e perpendicular ao elemento AB.
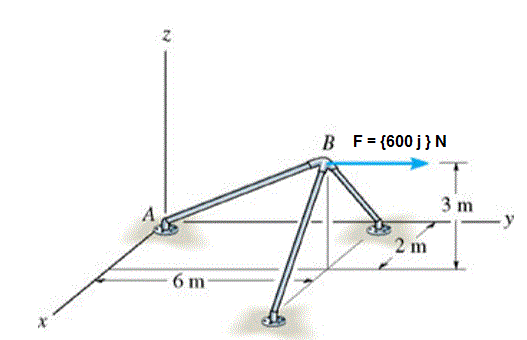
F// = 538 N
F_|_ = 345 N
F// = 498 N
F_|_ = 289 N
F// = 457 N
F_|_ = 290 N
F// = 514 N
F_|_ = 310 N
F// = 417 N
F_|_ = 280 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:
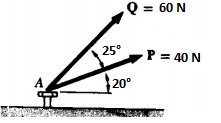
89,9 N e 22°
97,7 N e 30°
89,9 N e 35°
97,7 N e 35 °
68,5 N e 30°
O pendente de reboque AB está submetido à força de 50 kN exercida por um rebocador. Determine a força em cada um dos cabos de amarração, BC e BD, se o navio está se movendo para frente em velocidade constante.
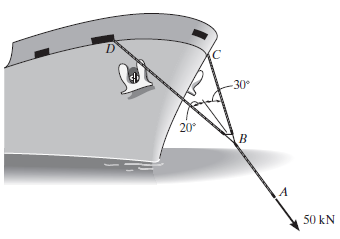
TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.
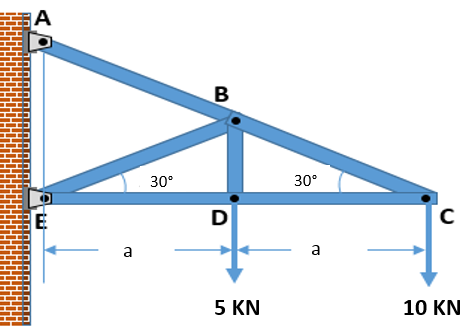
F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.
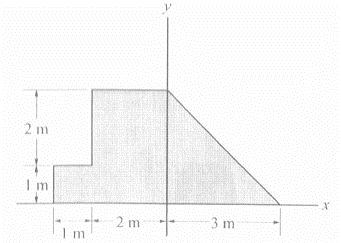

189,45 N
200,55 N
113,14 N
148,87 N
138,56 N
as forças normais FBC e FBD do esquema abaixo, são respectivamente:

14,14 KN e 10 KN
10 KN e - 13 KN
-14,14 KN e 13 KN
- 10 KN e 12 KN
-14,14 KN e - 10 KN
O cabo BD exerce no poste AC uma força P dirigida ao longo de BD. Se P tem uma componente de 150N perpendicular ao poste AC, então o valor da sua componente ao longo da linha AC será aproximadamente igual a

Dados: sen 40° = cos50° = 0,6428 e sen 50° = cos40° = 0,7661
195,82 N
178,75 N
189,45 N
213,50 N
199,57 N
Considere a figura a seguir,

O momento resultante produzido pelas forças em relação ao ponto O é aproximadamente
2,44 KN
1,29 KN
2,25 KN
2,77 KN
1,38 KN
Duas forças atuam sobre o gancho mostrado na figura. Especifique os ângulos (α,β,γ) diretores coordenados aproximados de F2, de modo que a força resultante FR atue ao longo do eixo y positivo e tenha intensidade de 700 N.

78°, 91° e 145°
63°, 163° e 123°
110°, 25° e 76°
46°, 28° e 34°
92°, 27° e 124°
A estrutura mostrada na figura está submetida a uma força horizontal. Determine a intensidade aproximada dos componentes dessa força, paralela e perpendicular ao elemento AB.

F// = 538 N
F_|_ = 345 N
F// = 498 N
F_|_ = 289 N
F// = 457 N
F_|_ = 290 N
F// = 514 N
F_|_ = 310 N
F// = 417 N
F_|_ = 280 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

89,9 N e 22°
97,7 N e 30°
89,9 N e 35°
97,7 N e 35 °
68,5 N e 30°
O pendente de reboque AB está submetido à força de 50 kN exercida por um rebocador. Determine a força em cada um dos cabos de amarração, BC e BD, se o navio está se movendo para frente em velocidade constante.

TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.

F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.


14,14 KN e 10 KN
10 KN e - 13 KN
-14,14 KN e 13 KN
- 10 KN e 12 KN
-14,14 KN e - 10 KN
O cabo BD exerce no poste AC uma força P dirigida ao longo de BD. Se P tem uma componente de 150N perpendicular ao poste AC, então o valor da sua componente ao longo da linha AC será aproximadamente igual a

Dados: sen 40° = cos50° = 0,6428 e sen 50° = cos40° = 0,7661
195,82 N
178,75 N
189,45 N
213,50 N
199,57 N
Considere a figura a seguir,

O momento resultante produzido pelas forças em relação ao ponto O é aproximadamente
2,44 KN
1,29 KN
2,25 KN
2,77 KN
1,38 KN
Duas forças atuam sobre o gancho mostrado na figura. Especifique os ângulos (α,β,γ) diretores coordenados aproximados de F2, de modo que a força resultante FR atue ao longo do eixo y positivo e tenha intensidade de 700 N.

78°, 91° e 145°
63°, 163° e 123°
110°, 25° e 76°
46°, 28° e 34°
92°, 27° e 124°
A estrutura mostrada na figura está submetida a uma força horizontal. Determine a intensidade aproximada dos componentes dessa força, paralela e perpendicular ao elemento AB.

F// = 538 N
F_|_ = 345 N
F// = 498 N
F_|_ = 289 N
F// = 457 N
F_|_ = 290 N
F// = 514 N
F_|_ = 310 N
F// = 417 N
F_|_ = 280 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

89,9 N e 22°
97,7 N e 30°
89,9 N e 35°
97,7 N e 35 °
68,5 N e 30°
O pendente de reboque AB está submetido à força de 50 kN exercida por um rebocador. Determine a força em cada um dos cabos de amarração, BC e BD, se o navio está se movendo para frente em velocidade constante.

TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.

F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.


195,82 N
178,75 N
189,45 N
213,50 N
199,57 N
Considere a figura a seguir,

O momento resultante produzido pelas forças em relação ao ponto O é aproximadamente
2,44 KN
1,29 KN
2,25 KN
2,77 KN
1,38 KN
Duas forças atuam sobre o gancho mostrado na figura. Especifique os ângulos (α,β,γ) diretores coordenados aproximados de F2, de modo que a força resultante FR atue ao longo do eixo y positivo e tenha intensidade de 700 N.

78°, 91° e 145°
63°, 163° e 123°
110°, 25° e 76°
46°, 28° e 34°
92°, 27° e 124°
A estrutura mostrada na figura está submetida a uma força horizontal. Determine a intensidade aproximada dos componentes dessa força, paralela e perpendicular ao elemento AB.

F// = 538 N
F_|_ = 345 N
F// = 498 N
F_|_ = 289 N
F// = 457 N
F_|_ = 290 N
F// = 514 N
F_|_ = 310 N
F// = 417 N
F_|_ = 280 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

89,9 N e 22°
97,7 N e 30°
89,9 N e 35°
97,7 N e 35 °
68,5 N e 30°
O pendente de reboque AB está submetido à força de 50 kN exercida por um rebocador. Determine a força em cada um dos cabos de amarração, BC e BD, se o navio está se movendo para frente em velocidade constante.

TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.

F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.


2,44 KN
1,29 KN
2,25 KN
2,77 KN
1,38 KN
Duas forças atuam sobre o gancho mostrado na figura. Especifique os ângulos (α,β,γ) diretores coordenados aproximados de F2, de modo que a força resultante FR atue ao longo do eixo y positivo e tenha intensidade de 700 N.

78°, 91° e 145°
63°, 163° e 123°
110°, 25° e 76°
46°, 28° e 34°
92°, 27° e 124°
A estrutura mostrada na figura está submetida a uma força horizontal. Determine a intensidade aproximada dos componentes dessa força, paralela e perpendicular ao elemento AB.

F// = 538 N
F_|_ = 345 N
F// = 498 N
F_|_ = 289 N
F// = 457 N
F_|_ = 290 N
F// = 514 N
F_|_ = 310 N
F// = 417 N
F_|_ = 280 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

89,9 N e 22°
97,7 N e 30°
89,9 N e 35°
97,7 N e 35 °
68,5 N e 30°
O pendente de reboque AB está submetido à força de 50 kN exercida por um rebocador. Determine a força em cada um dos cabos de amarração, BC e BD, se o navio está se movendo para frente em velocidade constante.

TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.

F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.


78°, 91° e 145°
63°, 163° e 123°
110°, 25° e 76°
46°, 28° e 34°
92°, 27° e 124°
A estrutura mostrada na figura está submetida a uma força horizontal. Determine a intensidade aproximada dos componentes dessa força, paralela e perpendicular ao elemento AB.

F// = 538 N
F_|_ = 345 N
F// = 498 N
F_|_ = 289 N
F// = 457 N
F_|_ = 290 N
F// = 514 N
F_|_ = 310 N
F// = 417 N
F_|_ = 280 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

89,9 N e 22°
97,7 N e 30°
89,9 N e 35°
97,7 N e 35 °
68,5 N e 30°
O pendente de reboque AB está submetido à força de 50 kN exercida por um rebocador. Determine a força em cada um dos cabos de amarração, BC e BD, se o navio está se movendo para frente em velocidade constante.

TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.

F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.


F// = 538 N
F_|_ = 345 N
F// = 498 N
F_|_ = 289 N
F// = 457 N
F_|_ = 290 N
F// = 514 N
F_|_ = 310 N
F// = 417 N
F_|_ = 280 N
As forças P e Q agem sobre um parafuso A, conforme figura abaixo. O valor da resultante e a direção são aproximadamente:

89,9 N e 22°
97,7 N e 30°
89,9 N e 35°
97,7 N e 35 °
68,5 N e 30°
O pendente de reboque AB está submetido à força de 50 kN exercida por um rebocador. Determine a força em cada um dos cabos de amarração, BC e BD, se o navio está se movendo para frente em velocidade constante.

TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.

F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.


89,9 N e 22°
97,7 N e 30°
89,9 N e 35°
97,7 N e 35 °
68,5 N e 30°
O pendente de reboque AB está submetido à força de 50 kN exercida por um rebocador. Determine a força em cada um dos cabos de amarração, BC e BD, se o navio está se movendo para frente em velocidade constante.

TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.

F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.


TBC = 20,8 kN, TBD = 40 kN
TBC = 12,3 kN, TBD = 24,5 kN
TBC = 14,3 kN, TBD = 29,6 kN
TBC = 22,3 kN, TBD = 32,6 kN
TBC = 43 kN, TBD = 28,6 kN
Calcule a força normal FCD e marque a opção correta.

F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.


F CD = 13,5 KN Compressão.
F CD = 12,43 KN Tração.
F CD = 15,5 KN Tração.
F CD = 17,32 KN Compressão.
F CD = 18,24 KN Compressão
Localize o centróide da área da placa mostrada abaixo.

