MATEMÁTICA INSTRUMENTAL
Jorge investiu R$ 800, 00 em um fundo cuja rentabilidade é de 2% ao mês. O valor acumulado, em R$, ao final de 10 meses é de aproximadamente:
1175,80
875,50
975,20
775,20
925,80
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,032x
f(x) = 0,032x -100
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = - 0,004x +100
Seja a uma função afim cuja forma é y = ax + b com a e b números reais. Se f(2) = 5 e f(-1)= -8, então a função f(x) pode ser representada por:
%7D%7D%7D%3D%5Cfrac%7B%7B-%7B11%7D%7Bx%7D-%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B13%7D%7Bx%7D%2B%7B11%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B13%7D%7Bx%7D-%7B11%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B11%7D%7Bx%7D%2B%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B-%7B11%7D%7Bx%7D%2B%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
O clima do Paraná está dividido em três tipos: no litoral e nas porções mais baixas do planalto, o clima é subtropical com chuvas bem distribuídas durante o ano e verões quentes; na porção mais elevada no estado, as chuvas são bem distribuídas durante o ano e os verões são amenos; por sua vez, no extremo noroeste do estado os verões são quentes e os invernos bem secos.
Disponível em<http://www.turismo.pr.gov.br/modules/conteudo/conteudo.php?conteudo=393>Acesso em 09/08/2017.
Em certo ano numa cidade do estado do Paraná, durante os dez primeiros dias do mês de julho de determinado ano, a temperatura, em °C, foi decrescendo de forma linear conforme a função  , em que t é o tempo medido em dias (onde t é maior ou igual a 1 e menor ou igual a 10) e T(t) é a temperatura em graus Celsius (°C).
, em que t é o tempo medido em dias (onde t é maior ou igual a 1 e menor ou igual a 10) e T(t) é a temperatura em graus Celsius (°C).
Nessas condições, pode-se afirmar que
no dia 8 de julho, a temperatura nessa cidade foi de 5°C.
no dia 10 de julho, a temperatura nessa cidade foi de 1°C.
no dia 4 de julho, a temperatura nessa cidade foi de 6°C.
no dia 2 de julho, a temperatura nessa cidade foi de 8°C.
no dia 1 de julho, a temperatura nessa cidade foi de 9°C.
Um tanque cuja capacidade total é de 2000 litros está completamente cheio de água às 8 horas. Entretanto, um furo na base provocou o vazamento constante do líquido. Sabendo que exatamente às 14 horas do mesmo dia o tanque continha 1760 litros, o tempo gasto para que o tanque atinja a metade da sua capacidade é de
30 h
10 h
15 h
25 h
20 h
Seja f(x) uma função afim cuja forma é f(x) = ax + b com a e b números reais e a diferente de 0. Se f(1) = 2 e f(-1)= -4, desta forma a função será representada por:
f(x) = x + 3
f(x) = 3x - 1
f(x) = 3x + 1
f(x) = x +1
f(x) = x -1
Dado o sistema de equações lineares 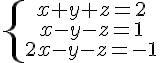 , podemos afirmar que
, podemos afirmar que
x = y.
Não existe solução.
x=2z
x=2; y =1 e z = 0
S = {1,2,3}.
Sejam a, b e c números reais positivos, com 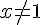 . Sobre a função logarítmica, analise os seguintes itens:
. Sobre a função logarítmica, analise os seguintes itens:
I.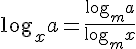
II. %7D%3D%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D-%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D)
III.%7D%3D%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D%5Cright)%7D.%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D%5Cright)%7D)
É correto o que se afirma em:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR 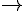 IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
1175,80
875,50
975,20
775,20
925,80
Muita gente já experimentou na prática a diferença que a altitude faz no tempo de fervura da água. Quanto mais alto estivermos em relação ao nível do mar, mais rapidamente a água entrará em ebulição. O valor da temperatura de ebulição da água é influenciado pela pressão atmosférica. Sabendo disso, analise a tabela, a seguir, que mostra a temperatura de ebulição da água em alguns locais em função da altitude:
Altitude (m)
Ponto de Ebulição da água (°C)
0
100
500
98
1000
96
Analisando os dados acima, podemos concluir que os mesmos satisfazem a função do tipo y = ax+b, em que x representa a altitude e y o ponto de ebulição.
A opção que representa a função y = f(x) é:
f(x) = - 0,032x
f(x) = 0,032x -100
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = - 0,004x +100
Seja a uma função afim cuja forma é y = ax + b com a e b números reais. Se f(2) = 5 e f(-1)= -8, então a função f(x) pode ser representada por:
%7D%7D%7D%3D%5Cfrac%7B%7B-%7B11%7D%7Bx%7D-%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B13%7D%7Bx%7D%2B%7B11%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B13%7D%7Bx%7D-%7B11%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B11%7D%7Bx%7D%2B%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B-%7B11%7D%7Bx%7D%2B%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
O clima do Paraná está dividido em três tipos: no litoral e nas porções mais baixas do planalto, o clima é subtropical com chuvas bem distribuídas durante o ano e verões quentes; na porção mais elevada no estado, as chuvas são bem distribuídas durante o ano e os verões são amenos; por sua vez, no extremo noroeste do estado os verões são quentes e os invernos bem secos.
Disponível em<http://www.turismo.pr.gov.br/modules/conteudo/conteudo.php?conteudo=393>Acesso em 09/08/2017.
Em certo ano numa cidade do estado do Paraná, durante os dez primeiros dias do mês de julho de determinado ano, a temperatura, em °C, foi decrescendo de forma linear conforme a função  , em que t é o tempo medido em dias (onde t é maior ou igual a 1 e menor ou igual a 10) e T(t) é a temperatura em graus Celsius (°C).
, em que t é o tempo medido em dias (onde t é maior ou igual a 1 e menor ou igual a 10) e T(t) é a temperatura em graus Celsius (°C).
Nessas condições, pode-se afirmar que
no dia 8 de julho, a temperatura nessa cidade foi de 5°C.
no dia 10 de julho, a temperatura nessa cidade foi de 1°C.
no dia 4 de julho, a temperatura nessa cidade foi de 6°C.
no dia 2 de julho, a temperatura nessa cidade foi de 8°C.
no dia 1 de julho, a temperatura nessa cidade foi de 9°C.
Um tanque cuja capacidade total é de 2000 litros está completamente cheio de água às 8 horas. Entretanto, um furo na base provocou o vazamento constante do líquido. Sabendo que exatamente às 14 horas do mesmo dia o tanque continha 1760 litros, o tempo gasto para que o tanque atinja a metade da sua capacidade é de
30 h
10 h
15 h
25 h
20 h
Seja f(x) uma função afim cuja forma é f(x) = ax + b com a e b números reais e a diferente de 0. Se f(1) = 2 e f(-1)= -4, desta forma a função será representada por:
f(x) = x + 3
f(x) = 3x - 1
f(x) = 3x + 1
f(x) = x +1
f(x) = x -1
Dado o sistema de equações lineares 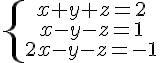 , podemos afirmar que
, podemos afirmar que
x = y.
Não existe solução.
x=2z
x=2; y =1 e z = 0
S = {1,2,3}.
Sejam a, b e c números reais positivos, com 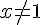 . Sobre a função logarítmica, analise os seguintes itens:
. Sobre a função logarítmica, analise os seguintes itens:
I.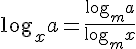
II. %7D%3D%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D-%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D)
III.%7D%3D%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D%5Cright)%7D.%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D%5Cright)%7D)
É correto o que se afirma em:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR 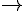 IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
f(x) = - 0,032x
f(x) = 0,032x -100
f(x) = 0,08x +100
f(x) = - 0,04x +100
f(x) = - 0,004x +100
Seja a uma função afim cuja forma é y = ax + b com a e b números reais. Se f(2) = 5 e f(-1)= -8, então a função f(x) pode ser representada por:
%7D%7D%7D%3D%5Cfrac%7B%7B-%7B11%7D%7Bx%7D-%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B13%7D%7Bx%7D%2B%7B11%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B13%7D%7Bx%7D-%7B11%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B%7B11%7D%7Bx%7D%2B%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
%7D%7D%7D%3D%5Cfrac%7B%7B-%7B11%7D%7Bx%7D%2B%7B13%7D%7D%7D%7B%7B3%7D%7D) .
.
O clima do Paraná está dividido em três tipos: no litoral e nas porções mais baixas do planalto, o clima é subtropical com chuvas bem distribuídas durante o ano e verões quentes; na porção mais elevada no estado, as chuvas são bem distribuídas durante o ano e os verões são amenos; por sua vez, no extremo noroeste do estado os verões são quentes e os invernos bem secos.
Disponível em<http://www.turismo.pr.gov.br/modules/conteudo/conteudo.php?conteudo=393>Acesso em 09/08/2017.
Em certo ano numa cidade do estado do Paraná, durante os dez primeiros dias do mês de julho de determinado ano, a temperatura, em °C, foi decrescendo de forma linear conforme a função  , em que t é o tempo medido em dias (onde t é maior ou igual a 1 e menor ou igual a 10) e T(t) é a temperatura em graus Celsius (°C).
, em que t é o tempo medido em dias (onde t é maior ou igual a 1 e menor ou igual a 10) e T(t) é a temperatura em graus Celsius (°C).
Nessas condições, pode-se afirmar que
no dia 8 de julho, a temperatura nessa cidade foi de 5°C.
no dia 10 de julho, a temperatura nessa cidade foi de 1°C.
no dia 4 de julho, a temperatura nessa cidade foi de 6°C.
no dia 2 de julho, a temperatura nessa cidade foi de 8°C.
no dia 1 de julho, a temperatura nessa cidade foi de 9°C.
Um tanque cuja capacidade total é de 2000 litros está completamente cheio de água às 8 horas. Entretanto, um furo na base provocou o vazamento constante do líquido. Sabendo que exatamente às 14 horas do mesmo dia o tanque continha 1760 litros, o tempo gasto para que o tanque atinja a metade da sua capacidade é de
30 h
10 h
15 h
25 h
20 h
Seja f(x) uma função afim cuja forma é f(x) = ax + b com a e b números reais e a diferente de 0. Se f(1) = 2 e f(-1)= -4, desta forma a função será representada por:
f(x) = x + 3
f(x) = 3x - 1
f(x) = 3x + 1
f(x) = x +1
f(x) = x -1
Dado o sistema de equações lineares 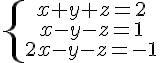 , podemos afirmar que
, podemos afirmar que
x = y.
Não existe solução.
x=2z
x=2; y =1 e z = 0
S = {1,2,3}.
Sejam a, b e c números reais positivos, com 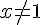 . Sobre a função logarítmica, analise os seguintes itens:
. Sobre a função logarítmica, analise os seguintes itens:
I.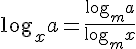
II. %7D%3D%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D-%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D)
III.%7D%3D%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D%5Cright)%7D.%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D%5Cright)%7D)
É correto o que se afirma em:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR 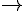 IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
.
.
.
.
.
O clima do Paraná está dividido em três tipos: no litoral e nas porções mais baixas do planalto, o clima é subtropical com chuvas bem distribuídas durante o ano e verões quentes; na porção mais elevada no estado, as chuvas são bem distribuídas durante o ano e os verões são amenos; por sua vez, no extremo noroeste do estado os verões são quentes e os invernos bem secos.
Disponível em<http://www.turismo.pr.gov.br/modules/conteudo/conteudo.php?conteudo=393>Acesso em 09/08/2017.
Em certo ano numa cidade do estado do Paraná, durante os dez primeiros dias do mês de julho de determinado ano, a temperatura, em °C, foi decrescendo de forma linear conforme a função  , em que t é o tempo medido em dias (onde t é maior ou igual a 1 e menor ou igual a 10) e T(t) é a temperatura em graus Celsius (°C).
, em que t é o tempo medido em dias (onde t é maior ou igual a 1 e menor ou igual a 10) e T(t) é a temperatura em graus Celsius (°C).
Nessas condições, pode-se afirmar que
no dia 8 de julho, a temperatura nessa cidade foi de 5°C.
no dia 10 de julho, a temperatura nessa cidade foi de 1°C.
no dia 4 de julho, a temperatura nessa cidade foi de 6°C.
no dia 2 de julho, a temperatura nessa cidade foi de 8°C.
no dia 1 de julho, a temperatura nessa cidade foi de 9°C.
Um tanque cuja capacidade total é de 2000 litros está completamente cheio de água às 8 horas. Entretanto, um furo na base provocou o vazamento constante do líquido. Sabendo que exatamente às 14 horas do mesmo dia o tanque continha 1760 litros, o tempo gasto para que o tanque atinja a metade da sua capacidade é de
30 h
10 h
15 h
25 h
20 h
Seja f(x) uma função afim cuja forma é f(x) = ax + b com a e b números reais e a diferente de 0. Se f(1) = 2 e f(-1)= -4, desta forma a função será representada por:
f(x) = x + 3
f(x) = 3x - 1
f(x) = 3x + 1
f(x) = x +1
f(x) = x -1
Dado o sistema de equações lineares 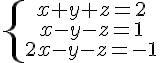 , podemos afirmar que
, podemos afirmar que
x = y.
Não existe solução.
x=2z
x=2; y =1 e z = 0
S = {1,2,3}.
Sejam a, b e c números reais positivos, com 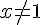 . Sobre a função logarítmica, analise os seguintes itens:
. Sobre a função logarítmica, analise os seguintes itens:
I.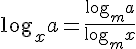
II. %7D%3D%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D-%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D)
III.%7D%3D%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D%5Cright)%7D.%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D%5Cright)%7D)
É correto o que se afirma em:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR 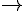 IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
no dia 8 de julho, a temperatura nessa cidade foi de 5°C.
no dia 10 de julho, a temperatura nessa cidade foi de 1°C.
no dia 4 de julho, a temperatura nessa cidade foi de 6°C.
no dia 2 de julho, a temperatura nessa cidade foi de 8°C.
no dia 1 de julho, a temperatura nessa cidade foi de 9°C.
Um tanque cuja capacidade total é de 2000 litros está completamente cheio de água às 8 horas. Entretanto, um furo na base provocou o vazamento constante do líquido. Sabendo que exatamente às 14 horas do mesmo dia o tanque continha 1760 litros, o tempo gasto para que o tanque atinja a metade da sua capacidade é de
30 h
10 h
15 h
25 h
20 h
Seja f(x) uma função afim cuja forma é f(x) = ax + b com a e b números reais e a diferente de 0. Se f(1) = 2 e f(-1)= -4, desta forma a função será representada por:
f(x) = x + 3
f(x) = 3x - 1
f(x) = 3x + 1
f(x) = x +1
f(x) = x -1
Dado o sistema de equações lineares 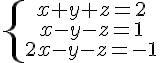 , podemos afirmar que
, podemos afirmar que
x = y.
Não existe solução.
x=2z
x=2; y =1 e z = 0
S = {1,2,3}.
Sejam a, b e c números reais positivos, com 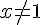 . Sobre a função logarítmica, analise os seguintes itens:
. Sobre a função logarítmica, analise os seguintes itens:
I.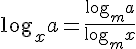
II. %7D%3D%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D-%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D)
III.%7D%3D%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D%5Cright)%7D.%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D%5Cright)%7D)
É correto o que se afirma em:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR  IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
30 h
10 h
15 h
25 h
20 h
Seja f(x) uma função afim cuja forma é f(x) = ax + b com a e b números reais e a diferente de 0. Se f(1) = 2 e f(-1)= -4, desta forma a função será representada por:
f(x) = x + 3
f(x) = 3x - 1
f(x) = 3x + 1
f(x) = x +1
f(x) = x -1
Dado o sistema de equações lineares 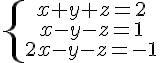 , podemos afirmar que
, podemos afirmar que
x = y.
Não existe solução.
x=2z
x=2; y =1 e z = 0
S = {1,2,3}.
Sejam a, b e c números reais positivos, com 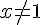 . Sobre a função logarítmica, analise os seguintes itens:
. Sobre a função logarítmica, analise os seguintes itens:
I.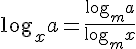
II. %7D%3D%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D-%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D)
III.%7D%3D%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D%5Cright)%7D.%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D%5Cright)%7D)
É correto o que se afirma em:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR 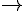 IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
f(x) = x + 3
f(x) = 3x - 1
f(x) = 3x + 1
f(x) = x +1
f(x) = x -1
Dado o sistema de equações lineares 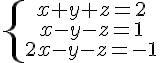 , podemos afirmar que
, podemos afirmar que
x = y.
Não existe solução.
x=2z
x=2; y =1 e z = 0
S = {1,2,3}.
Sejam a, b e c números reais positivos, com 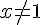 . Sobre a função logarítmica, analise os seguintes itens:
. Sobre a função logarítmica, analise os seguintes itens:
I.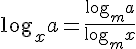
II. %7D%3D%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D-%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D)
III.%7D%3D%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D%5Cright)%7D.%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D%5Cright)%7D)
É correto o que se afirma em:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR 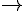 IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
x = y.
Não existe solução.
x=2z
x=2; y =1 e z = 0
S = {1,2,3}.
Sejam a, b e c números reais positivos, com 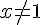 . Sobre a função logarítmica, analise os seguintes itens:
. Sobre a função logarítmica, analise os seguintes itens:
I.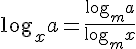
II. %7D%3D%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D-%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D)
III.%7D%3D%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Ba%7D%5Cright)%7D.%7B%5Cleft(%7B%5Clog%7D_%7B%7Bx%7D%7D%7Bb%7D%5Cright)%7D)
É correto o que se afirma em:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR 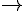 IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
I e III apenas
II apenas
I e II apenas
I apenas
I, II e III apenas
Considere a função f: IR 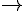 IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
IR definida por f(x) = 2x +5 , analise as afirmativas a seguir:
I. A função representada é decrescente, pois a < 0;
II. O ponto onde a função intercepta o eixo y é ( 0, 3);
III. O ponto onde a função intercepta o eixo x é (- 5/2, 0).
E correto o que se afirma em
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.
A função afim representada por L(t) = at + b, onde L expressa o lucro de uma empresa, em milhões de reais e o t indica o tempo em meses, de um determinado período. Nessas condições, sabendo que L(2) = 200 e L(4) = 340. O lucro obtido por essa empresa, no período de dois anos será de:
I, apenas.
I, II e III.
I e III, apenas.
II, apenas.
III, apenas.