MATEMÁTICA III
Um móvel parte da origem do arco na circunferência trigonométrica e percorre 111 915°. O número de voltas completas e o quadrante em que está a extremidade do arco pode ser indicado respectivamente em:
310 ; 1°
290 ; 4°
310 ; 4°
290 ; 3°
310 ; 2°
Com 2500 voltas efetuadas pelos pneus, o automóvel percorre 3454 metros. Adote  .
.
O raio dos pneus das rodas é exatamente igual a:
25 cm
0,16 cm
22 cm
16 cm
0, 22 cm
A figura a seguir demarca alguns ângulos do ciclo trigonométrico,

Podemos afirmar que,
I) A + N = 380°
II) P – N = 90°
III) N – K = 150°
IV) C = 150°
Assinale a opção verdadeira:
II e III são verdadeiras
IV é falsa
I e II são falsas
I e IV são falsas
II é verdadeiro
Se %7D%7D%7D%3D%7B33%7D) e
e  então o valor de
então o valor de  é exatamente:
é exatamente:
0,1
0,3
0,4
0,33
0,2
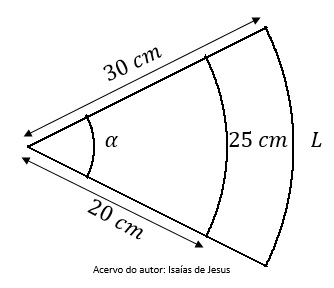
Dada uma circunferência de centro O, raio r e dois pontos A e B pertencentes à circunferência, temos que a distância entre os pontos assinalados é um arco de circunferência. O comprimento de um arco é proporcional à medida do ângulo central dado por: .
.
O comprimento de um arco com ângulo central igual a 30º, contido numa circunferência de raio 2 cm é aproximadamente
1,10 cm
1,85 cm
1,55 cm
2,09 cm
1,05 cm
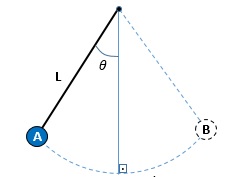
Considere a figura a seguir:
Os valores de L e  são respectivamente:
são respectivamente:
35 cm e 1,25 rad.
37,5 cm e 1,25 rad.
37,5 cm e 12,5 rad.
37,5 cm e 1,5 rad.
35 cm e 1 rad.
O domínio e imagem da função y = f(x) = sec(x) são respectivamente:
 e
e ![Im = ]-oo,1]uu[1,+oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e ![Im = ]-oo, -1[ uu]1,+oo]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5Cleft%5B%5Ccup%5Cright%5D%7D%7B1%7D%2C%2B%5Cinfty%7B%5C%5D%7D)
 e
e ![Im=]-oo,-1] uu [1, +oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e 
 e
e ![Im=[-1,1]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5Cleft%5B-%7B1%7D%2C%7B1%7D%5Cright%5D%7D)
A função tangente é obtida considerando uma volta completa no ciclo trigonométrico. O que podemos afirmar sobre os valores da tg(900) e tg(2700), respectivamente?
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,
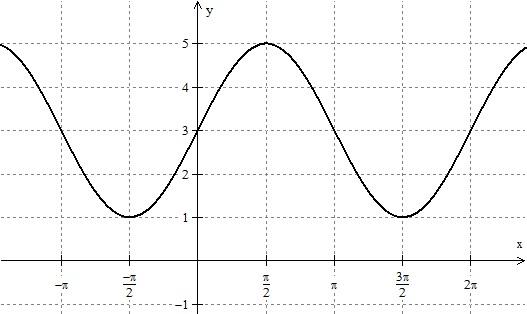
O gráfico dado corresponde à função:
310 ; 1°
290 ; 4°
310 ; 4°
290 ; 3°
310 ; 2°
Com 2500 voltas efetuadas pelos pneus, o automóvel percorre 3454 metros. Adote  .
.
O raio dos pneus das rodas é exatamente igual a:
25 cm
0,16 cm
22 cm
16 cm
0, 22 cm
A figura a seguir demarca alguns ângulos do ciclo trigonométrico,

Podemos afirmar que,
I) A + N = 380°
II) P – N = 90°
III) N – K = 150°
IV) C = 150°
Assinale a opção verdadeira:
II e III são verdadeiras
IV é falsa
I e II são falsas
I e IV são falsas
II é verdadeiro
Se %7D%7D%7D%3D%7B33%7D) e
e  então o valor de
então o valor de  é exatamente:
é exatamente:
0,1
0,3
0,4
0,33
0,2
Dada uma circunferência de centro O, raio r e dois pontos A e B pertencentes à circunferência, temos que a distância entre os pontos assinalados é um arco de circunferência. O comprimento de um arco é proporcional à medida do ângulo central dado por: .
.
O comprimento de um arco com ângulo central igual a 30º, contido numa circunferência de raio 2 cm é aproximadamente
1,10 cm
1,85 cm
1,55 cm
2,09 cm
1,05 cm
Considere a figura a seguir:

Os valores de L e  são respectivamente:
são respectivamente:
35 cm e 1,25 rad.
37,5 cm e 1,25 rad.
37,5 cm e 12,5 rad.
37,5 cm e 1,5 rad.
35 cm e 1 rad.
O domínio e imagem da função y = f(x) = sec(x) são respectivamente:
 e
e ![Im = ]-oo,1]uu[1,+oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e ![Im = ]-oo, -1[ uu]1,+oo]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5Cleft%5B%5Ccup%5Cright%5D%7D%7B1%7D%2C%2B%5Cinfty%7B%5C%5D%7D)
 e
e ![Im=]-oo,-1] uu [1, +oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e 
 e
e ![Im=[-1,1]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5Cleft%5B-%7B1%7D%2C%7B1%7D%5Cright%5D%7D)
A função tangente é obtida considerando uma volta completa no ciclo trigonométrico. O que podemos afirmar sobre os valores da tg(900) e tg(2700), respectivamente?
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,

O gráfico dado corresponde à função:
25 cm
0,16 cm
22 cm
16 cm
0, 22 cm
A figura a seguir demarca alguns ângulos do ciclo trigonométrico,

Podemos afirmar que,
I) A + N = 380°
II) P – N = 90°
III) N – K = 150°
IV) C = 150°
Assinale a opção verdadeira:
II e III são verdadeiras
IV é falsa
I e II são falsas
I e IV são falsas
II é verdadeiro
Se %7D%7D%7D%3D%7B33%7D) e
e  então o valor de
então o valor de  é exatamente:
é exatamente:
0,1
0,3
0,4
0,33
0,2
Dada uma circunferência de centro O, raio r e dois pontos A e B pertencentes à circunferência, temos que a distância entre os pontos assinalados é um arco de circunferência. O comprimento de um arco é proporcional à medida do ângulo central dado por: .
.
O comprimento de um arco com ângulo central igual a 30º, contido numa circunferência de raio 2 cm é aproximadamente
1,10 cm
1,85 cm
1,55 cm
2,09 cm
1,05 cm
Considere a figura a seguir:

Os valores de L e  são respectivamente:
são respectivamente:
35 cm e 1,25 rad.
37,5 cm e 1,25 rad.
37,5 cm e 12,5 rad.
37,5 cm e 1,5 rad.
35 cm e 1 rad.
O domínio e imagem da função y = f(x) = sec(x) são respectivamente:
 e
e ![Im = ]-oo,1]uu[1,+oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e ![Im = ]-oo, -1[ uu]1,+oo]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5Cleft%5B%5Ccup%5Cright%5D%7D%7B1%7D%2C%2B%5Cinfty%7B%5C%5D%7D)
 e
e ![Im=]-oo,-1] uu [1, +oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e 
 e
e ![Im=[-1,1]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5Cleft%5B-%7B1%7D%2C%7B1%7D%5Cright%5D%7D)
A função tangente é obtida considerando uma volta completa no ciclo trigonométrico. O que podemos afirmar sobre os valores da tg(900) e tg(2700), respectivamente?
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,

O gráfico dado corresponde à função:

II e III são verdadeiras
IV é falsa
I e II são falsas
I e IV são falsas
II é verdadeiro
Se %7D%7D%7D%3D%7B33%7D) e
e  então o valor de
então o valor de  é exatamente:
é exatamente:
0,1
0,3
0,4
0,33
0,2
Dada uma circunferência de centro O, raio r e dois pontos A e B pertencentes à circunferência, temos que a distância entre os pontos assinalados é um arco de circunferência. O comprimento de um arco é proporcional à medida do ângulo central dado por: .
.
O comprimento de um arco com ângulo central igual a 30º, contido numa circunferência de raio 2 cm é aproximadamente
1,10 cm
1,85 cm
1,55 cm
2,09 cm
1,05 cm
Considere a figura a seguir:

Os valores de L e  são respectivamente:
são respectivamente:
35 cm e 1,25 rad.
37,5 cm e 1,25 rad.
37,5 cm e 12,5 rad.
37,5 cm e 1,5 rad.
35 cm e 1 rad.
O domínio e imagem da função y = f(x) = sec(x) são respectivamente:
 e
e ![Im = ]-oo,1]uu[1,+oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e ![Im = ]-oo, -1[ uu]1,+oo]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5Cleft%5B%5Ccup%5Cright%5D%7D%7B1%7D%2C%2B%5Cinfty%7B%5C%5D%7D)
 e
e ![Im=]-oo,-1] uu [1, +oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e 
 e
e ![Im=[-1,1]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5Cleft%5B-%7B1%7D%2C%7B1%7D%5Cright%5D%7D)
A função tangente é obtida considerando uma volta completa no ciclo trigonométrico. O que podemos afirmar sobre os valores da tg(900) e tg(2700), respectivamente?
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,

O gráfico dado corresponde à função:
0,1
0,3
0,4
0,33
0,2
Dada uma circunferência de centro O, raio r e dois pontos A e B pertencentes à circunferência, temos que a distância entre os pontos assinalados é um arco de circunferência. O comprimento de um arco é proporcional à medida do ângulo central dado por: .
.
O comprimento de um arco com ângulo central igual a 30º, contido numa circunferência de raio 2 cm é aproximadamente
1,10 cm
1,85 cm
1,55 cm
2,09 cm
1,05 cm
Considere a figura a seguir:

Os valores de L e  são respectivamente:
são respectivamente:
35 cm e 1,25 rad.
37,5 cm e 1,25 rad.
37,5 cm e 12,5 rad.
37,5 cm e 1,5 rad.
35 cm e 1 rad.
O domínio e imagem da função y = f(x) = sec(x) são respectivamente:
 e
e ![Im = ]-oo,1]uu[1,+oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e ![Im = ]-oo, -1[ uu]1,+oo]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5Cleft%5B%5Ccup%5Cright%5D%7D%7B1%7D%2C%2B%5Cinfty%7B%5C%5D%7D)
 e
e ![Im=]-oo,-1] uu [1, +oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e 
 e
e ![Im=[-1,1]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5Cleft%5B-%7B1%7D%2C%7B1%7D%5Cright%5D%7D)
A função tangente é obtida considerando uma volta completa no ciclo trigonométrico. O que podemos afirmar sobre os valores da tg(900) e tg(2700), respectivamente?
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,

O gráfico dado corresponde à função:
1,10 cm
1,85 cm
1,55 cm
2,09 cm
1,05 cm
Considere a figura a seguir:

Os valores de L e  são respectivamente:
são respectivamente:
35 cm e 1,25 rad.
37,5 cm e 1,25 rad.
37,5 cm e 12,5 rad.
37,5 cm e 1,5 rad.
35 cm e 1 rad.
O domínio e imagem da função y = f(x) = sec(x) são respectivamente:
 e
e ![Im = ]-oo,1]uu[1,+oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e ![Im = ]-oo, -1[ uu]1,+oo]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5Cleft%5B%5Ccup%5Cright%5D%7D%7B1%7D%2C%2B%5Cinfty%7B%5C%5D%7D)
 e
e ![Im=]-oo,-1] uu [1, +oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e 
 e
e ![Im=[-1,1]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5Cleft%5B-%7B1%7D%2C%7B1%7D%5Cright%5D%7D)
A função tangente é obtida considerando uma volta completa no ciclo trigonométrico. O que podemos afirmar sobre os valores da tg(900) e tg(2700), respectivamente?
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,

O gráfico dado corresponde à função:

35 cm e 1,25 rad.
37,5 cm e 1,25 rad.
37,5 cm e 12,5 rad.
37,5 cm e 1,5 rad.
35 cm e 1 rad.
O domínio e imagem da função y = f(x) = sec(x) são respectivamente:
 e
e ![Im = ]-oo,1]uu[1,+oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e ![Im = ]-oo, -1[ uu]1,+oo]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5Cleft%5B%5Ccup%5Cright%5D%7D%7B1%7D%2C%2B%5Cinfty%7B%5C%5D%7D)
 e
e ![Im=]-oo,-1] uu [1, +oo[](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B1%7D%7B%5C%5D%7D%5Ccup%7B%5Cleft%5B%7B1%7D%2C%2B%5Cinfty%7B%5B%7D%5Cright.%7D)
 e
e 
 e
e ![Im=[-1,1]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5Cleft%5B-%7B1%7D%2C%7B1%7D%5Cright%5D%7D)
A função tangente é obtida considerando uma volta completa no ciclo trigonométrico. O que podemos afirmar sobre os valores da tg(900) e tg(2700), respectivamente?
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,

O gráfico dado corresponde à função:
A função tangente é obtida considerando uma volta completa no ciclo trigonométrico. O que podemos afirmar sobre os valores da tg(900) e tg(2700), respectivamente?
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,

O gráfico dado corresponde à função:
tg(900) = 1 e tg(2700) = 1
tg(900) = 1 e tg(2700) = - 1
tg(900) = 1 e tg(2700) = 0
tg(900) não existe e tg(2700) não existe
tg(900) = 0 e tg(2700) = - 1
Considere o gráfico abaixo,

O gráfico dado corresponde à função: