MATEMÁTICA III
Sabendo que senx = -3/5 e cosx = 4/5, então:
e secx = 5/4.
e tgx = 1.
e tgx = -3/4.
e cotgx = -4/3 .
e cossecx = -5/3.
Observe o gráfico apresentado a seguir e defina seu Período e Imagem.
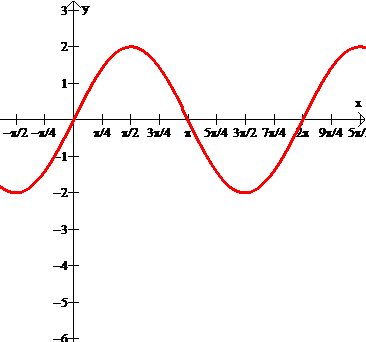
Período 
e Imagem=[-2,2]
Período 
e Imagem=[1,2]
Período 
e Imagem=[-2,2]
Período e Imagem=[-1,2]
Período e Imagem=[-2,2]
Sendo senx = -1/2, com x no terceiro quadrante, então é correto afirmar que:
tgx > senx > cosx
senx > tgx > cosx
cosx > tgx > senx
senx > cosx > tgx
cosx > senx > tgx
Um pêndulo de um relógio tem comprimento L metros e executa o movimento de A para B indicado na figura.
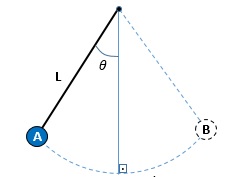
Se L = 0,6 m e 
= 40° então o comprimento do arco AB é aproximadamente:
Adote: 
.
0,042 m
83,7 cm
83,7 m
0,837 cm
8,37 m
Um trabalhador precisa fazer cercar um terreno, a figura que representa as dimensões do terreno segue abaixo:
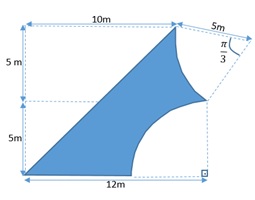
O perímetro desse terreno é aproximadamente
Obs. o comprimento angular pi/3 = 60°.
31 metros.
34 metros.
41 metros.
38 metros.
40 metros.
O gráfico a seguir, representa a função:
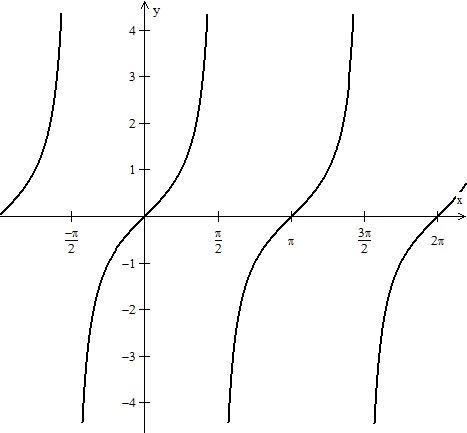
y = tg(x)
y = cos(x)
y = cotg(x)
y = - cotg(x)
y = - tg(x)
Sendo 
e 
com x no 4° quadrante, então:
M = - 5
M = 5
M = 1/5
M = -1/5
M = 25
Seja 
o comprimento de um arco dado por 
em que, 
é a medida em graus de um arco e 
o raio de uma circunferência, determine o comprimento de um arco de 72° que tem 20 cm de raio.
A resposta aproximada está na opção:
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
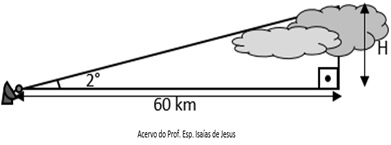
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
e secx = 5/4.
e tgx = 1.
e tgx = -3/4.
e cotgx = -4/3 .
e cossecx = -5/3.
Observe o gráfico apresentado a seguir e defina seu Período e Imagem.
Período e Imagem=[-2,2]
Período e Imagem=[1,2]
Período e Imagem=[-2,2]
Período e Imagem=[-1,2]
Período e Imagem=[-2,2]
Sendo senx = -1/2, com x no terceiro quadrante, então é correto afirmar que:
tgx > senx > cosx
senx > tgx > cosx
cosx > tgx > senx
senx > cosx > tgx
cosx > senx > tgx
Um pêndulo de um relógio tem comprimento L metros e executa o movimento de A para B indicado na figura.
Se L = 0,6 m e = 40° então o comprimento do arco AB é aproximadamente:
Adote: .
0,042 m
83,7 cm
83,7 m
0,837 cm
8,37 m
Um trabalhador precisa fazer cercar um terreno, a figura que representa as dimensões do terreno segue abaixo:
O perímetro desse terreno é aproximadamente
Obs. o comprimento angular pi/3 = 60°.
31 metros.
34 metros.
41 metros.
38 metros.
40 metros.
O gráfico a seguir, representa a função:
y = tg(x)
y = cos(x)
y = cotg(x)
y = - cotg(x)
y = - tg(x)
Sendo e com x no 4° quadrante, então:
M = - 5
M = 5
M = 1/5
M = -1/5
M = 25
Seja o comprimento de um arco dado por em que, é a medida em graus de um arco e o raio de uma circunferência, determine o comprimento de um arco de 72° que tem 20 cm de raio.
A resposta aproximada está na opção:
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
Período e Imagem=[-2,2]
Período e Imagem=[1,2]
Período e Imagem=[-2,2]
Período e Imagem=[-1,2]
Período e Imagem=[-2,2]
Sendo senx = -1/2, com x no terceiro quadrante, então é correto afirmar que:
tgx > senx > cosx
senx > tgx > cosx
cosx > tgx > senx
senx > cosx > tgx
cosx > senx > tgx
Um pêndulo de um relógio tem comprimento L metros e executa o movimento de A para B indicado na figura.
Se L = 0,6 m e = 40° então o comprimento do arco AB é aproximadamente:
Adote: .
0,042 m
83,7 cm
83,7 m
0,837 cm
8,37 m
Um trabalhador precisa fazer cercar um terreno, a figura que representa as dimensões do terreno segue abaixo:
O perímetro desse terreno é aproximadamente
Obs. o comprimento angular pi/3 = 60°.
31 metros.
34 metros.
41 metros.
38 metros.
40 metros.
O gráfico a seguir, representa a função:
y = tg(x)
y = cos(x)
y = cotg(x)
y = - cotg(x)
y = - tg(x)
Sendo e com x no 4° quadrante, então:
M = - 5
M = 5
M = 1/5
M = -1/5
M = 25
Seja o comprimento de um arco dado por em que, é a medida em graus de um arco e o raio de uma circunferência, determine o comprimento de um arco de 72° que tem 20 cm de raio.
A resposta aproximada está na opção:
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
tgx > senx > cosx
senx > tgx > cosx
cosx > tgx > senx
senx > cosx > tgx
cosx > senx > tgx
Um pêndulo de um relógio tem comprimento L metros e executa o movimento de A para B indicado na figura.
Se L = 0,6 m e = 40° então o comprimento do arco AB é aproximadamente:
Adote: .
0,042 m
83,7 cm
83,7 m
0,837 cm
8,37 m
Um trabalhador precisa fazer cercar um terreno, a figura que representa as dimensões do terreno segue abaixo:
O perímetro desse terreno é aproximadamente
Obs. o comprimento angular pi/3 = 60°.
31 metros.
34 metros.
41 metros.
38 metros.
40 metros.
O gráfico a seguir, representa a função:
y = tg(x)
y = cos(x)
y = cotg(x)
y = - cotg(x)
y = - tg(x)
Sendo e com x no 4° quadrante, então:
M = - 5
M = 5
M = 1/5
M = -1/5
M = 25
Seja o comprimento de um arco dado por em que, é a medida em graus de um arco e o raio de uma circunferência, determine o comprimento de um arco de 72° que tem 20 cm de raio.
A resposta aproximada está na opção:
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
0,042 m
83,7 cm
83,7 m
0,837 cm
8,37 m
Um trabalhador precisa fazer cercar um terreno, a figura que representa as dimensões do terreno segue abaixo:
O perímetro desse terreno é aproximadamente
Obs. o comprimento angular pi/3 = 60°.
31 metros.
34 metros.
41 metros.
38 metros.
40 metros.
O gráfico a seguir, representa a função:
y = tg(x)
y = cos(x)
y = cotg(x)
y = - cotg(x)
y = - tg(x)
Sendo e com x no 4° quadrante, então:
M = - 5
M = 5
M = 1/5
M = -1/5
M = 25
Seja o comprimento de um arco dado por em que, é a medida em graus de um arco e o raio de uma circunferência, determine o comprimento de um arco de 72° que tem 20 cm de raio.
A resposta aproximada está na opção:
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
31 metros.
34 metros.
41 metros.
38 metros.
40 metros.
O gráfico a seguir, representa a função:
y = tg(x)
y = cos(x)
y = cotg(x)
y = - cotg(x)
y = - tg(x)
Sendo e com x no 4° quadrante, então:
M = - 5
M = 5
M = 1/5
M = -1/5
M = 25
Seja o comprimento de um arco dado por em que, é a medida em graus de um arco e o raio de uma circunferência, determine o comprimento de um arco de 72° que tem 20 cm de raio.
A resposta aproximada está na opção:
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
y = tg(x)
y = cos(x)
y = cotg(x)
y = - cotg(x)
y = - tg(x)
Sendo e com x no 4° quadrante, então:
M = - 5
M = 5
M = 1/5
M = -1/5
M = 25
Seja o comprimento de um arco dado por em que, é a medida em graus de um arco e o raio de uma circunferência, determine o comprimento de um arco de 72° que tem 20 cm de raio.
A resposta aproximada está na opção:
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
M = - 5
M = 5
M = 1/5
M = -1/5
M = 25
Seja o comprimento de um arco dado por em que, é a medida em graus de um arco e o raio de uma circunferência, determine o comprimento de um arco de 72° que tem 20 cm de raio.
A resposta aproximada está na opção:
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
20, 34 cm
19, 43 cm
25,13 cm
26, 74 cm
24, 63 cm
Um radar mede a altura de uma nuvem em relação ao solo, para previsões meteorológicas e orientar aviões para que se evitem turbulências, e, consequentemente, acidentes.
Conforme figura abaixo:
A altura H da nuvem detectada pelo radar é aproximadamente:
(Dados: sen 2º = 0,03489, cos 2º= 0,99939 e tg 2º=0,03492).
.jpg)