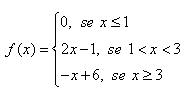MATEMÁTICA II
Suponha que, em janeiro de 2017, o PIB (Produto Interno Bruto) de um país seja de 700 bilhões de dólares. Se o PIB crescer 2% ao ano, de forma cumulativa, o PIB do país em janeiro de 2022, será de aproximadamente:
793 bilhões.
779 bilhões.
772,9 bilhões.
723,1 bilhões.
463,6 bilhões.
Determinados bens, principalmente objetos de uso contínuo, sofrem desvalorização comercial em função do desgaste natural ao longo do tempo. O estado de conservação desses objetos influencia na venda futura, condicionando valores acima dos índices percentuais de depreciação.
O cálculo da depreciação de um objeto é realizado de acordo com uma taxa percentual de desvalorização anual.
Considere que a expressão matemática a seguir represente o valor depreciado:

Vd = valor depreciado ; Vp = valor pago ; i = taxa de depreciação ; t = tempo decorrido em anos ; Qr = quilômetro rodado
O valor de um automóvel novo é exatamente R$ 40.000,00. Considerando que a taxa de depreciação desse automóvel é equivalente a 9% ao ano, e que anualmente há previsão de rodar 10000 quilômetros. O valor em R$ do automóvel daqui a 8 anos será aproximadamente
21360,20
22189,90
78702,50
18810,01
39350,25
Seja a função%7D%7D%7D%3D%7B2%7D%7Bx%7D-%7B3%7D) uma função bijetora, então a função f -1(x) será definida por:
uma função bijetora, então a função f -1(x) será definida por:
%7D%3D%7B2%7D%7Bx%7D%2B%7B3%7D)
%7D%3D%7B3%7D%7Bx%7D-%7B2%7D)
%7D%3D%5Cfrac%7B%7B-%7Bx%7D%2B%7B3%7D%7D%7D%7B%7B2%7D%7D)
%7D%3D%5Cfrac%7B%7B%7B3%7D%7Bx%7D-%7B2%7D%7D%7D%7B%7B2%7D%7D)
%7D%3D%5Cfrac%7B%7B%7Bx%7D%2B%7B3%7D%7D%7D%7B%7B2%7D%7D)

Se Comprar 48 livros pagarei uma quantia maior que se comprar 49 livros.
Comprando 20 livros pagarei 50% do valor que equivale a comprar 40 livros.
Comprando 30 livros pagarei um quantia de 340.
Comprar 24 livros é mais barato que comprar 25.
Comprando 20 livros pagarei um quantia de 284.
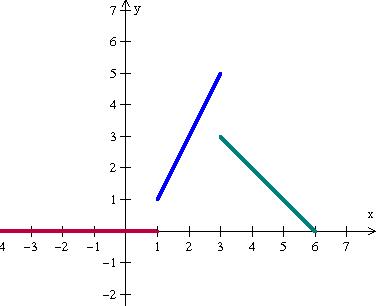
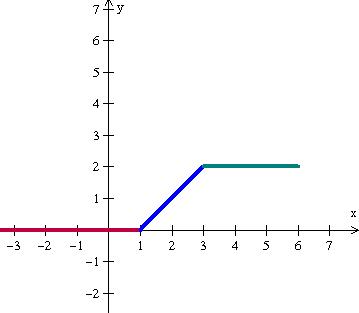
O domínio e a imagem de uma função definida em várias sentenças, é a união dos domínios e das imagens das sentenças.
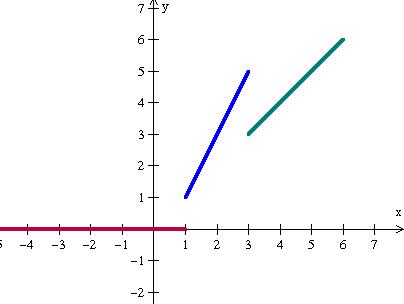
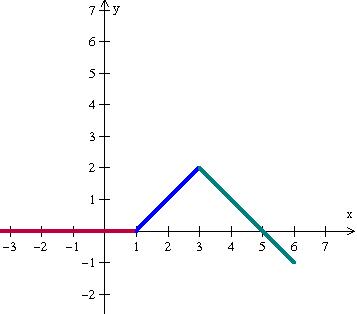
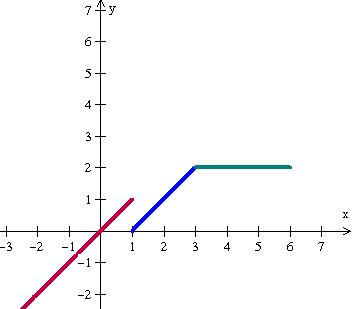
Considere a função f(x) e seu esboço gráfico:
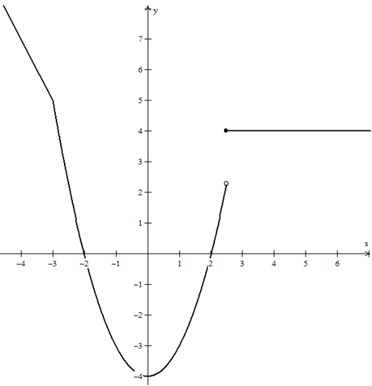
O domínio D(f) e a Im(f) são respectivamente:
793 bilhões.
779 bilhões.
772,9 bilhões.
723,1 bilhões.
463,6 bilhões.
Determinados bens, principalmente objetos de uso contínuo, sofrem desvalorização comercial em função do desgaste natural ao longo do tempo. O estado de conservação desses objetos influencia na venda futura, condicionando valores acima dos índices percentuais de depreciação.
O cálculo da depreciação de um objeto é realizado de acordo com uma taxa percentual de desvalorização anual.
Considere que a expressão matemática a seguir represente o valor depreciado:

Vd = valor depreciado ; Vp = valor pago ; i = taxa de depreciação ; t = tempo decorrido em anos ; Qr = quilômetro rodado
O valor de um automóvel novo é exatamente R$ 40.000,00. Considerando que a taxa de depreciação desse automóvel é equivalente a 9% ao ano, e que anualmente há previsão de rodar 10000 quilômetros. O valor em R$ do automóvel daqui a 8 anos será aproximadamente
21360,20
22189,90
78702,50
18810,01
39350,25
Seja a função%7D%7D%7D%3D%7B2%7D%7Bx%7D-%7B3%7D) uma função bijetora, então a função f -1(x) será definida por:
uma função bijetora, então a função f -1(x) será definida por:
%7D%3D%7B2%7D%7Bx%7D%2B%7B3%7D)
%7D%3D%7B3%7D%7Bx%7D-%7B2%7D)
%7D%3D%5Cfrac%7B%7B-%7Bx%7D%2B%7B3%7D%7D%7D%7B%7B2%7D%7D)
%7D%3D%5Cfrac%7B%7B%7B3%7D%7Bx%7D-%7B2%7D%7D%7D%7B%7B2%7D%7D)
%7D%3D%5Cfrac%7B%7B%7Bx%7D%2B%7B3%7D%7D%7D%7B%7B2%7D%7D)

Se Comprar 48 livros pagarei uma quantia maior que se comprar 49 livros.
Comprando 20 livros pagarei 50% do valor que equivale a comprar 40 livros.
Comprando 30 livros pagarei um quantia de 340.
Comprar 24 livros é mais barato que comprar 25.
Comprando 20 livros pagarei um quantia de 284.
O domínio e a imagem de uma função definida em várias sentenças, é a união dos domínios e das imagens das sentenças.
Considere a função f(x) e seu esboço gráfico:

O domínio D(f) e a Im(f) são respectivamente:
21360,20
22189,90
78702,50
18810,01
39350,25
Seja a função%7D%7D%7D%3D%7B2%7D%7Bx%7D-%7B3%7D) uma função bijetora, então a função f -1(x) será definida por:
uma função bijetora, então a função f -1(x) será definida por:
%7D%3D%7B2%7D%7Bx%7D%2B%7B3%7D)
%7D%3D%7B3%7D%7Bx%7D-%7B2%7D)
%7D%3D%5Cfrac%7B%7B-%7Bx%7D%2B%7B3%7D%7D%7D%7B%7B2%7D%7D)
%7D%3D%5Cfrac%7B%7B%7B3%7D%7Bx%7D-%7B2%7D%7D%7D%7B%7B2%7D%7D)
%7D%3D%5Cfrac%7B%7B%7Bx%7D%2B%7B3%7D%7D%7D%7B%7B2%7D%7D)

Se Comprar 48 livros pagarei uma quantia maior que se comprar 49 livros.
Comprando 20 livros pagarei 50% do valor que equivale a comprar 40 livros.
Comprando 30 livros pagarei um quantia de 340.
Comprar 24 livros é mais barato que comprar 25.
Comprando 20 livros pagarei um quantia de 284.
O domínio e a imagem de uma função definida em várias sentenças, é a união dos domínios e das imagens das sentenças.
Considere a função f(x) e seu esboço gráfico:

O domínio D(f) e a Im(f) são respectivamente:

Se Comprar 48 livros pagarei uma quantia maior que se comprar 49 livros.
Comprando 20 livros pagarei 50% do valor que equivale a comprar 40 livros.
Comprando 30 livros pagarei um quantia de 340.
Comprar 24 livros é mais barato que comprar 25.
Comprando 20 livros pagarei um quantia de 284.
O domínio e a imagem de uma função definida em várias sentenças, é a união dos domínios e das imagens das sentenças.
Considere a função f(x) e seu esboço gráfico:

O domínio D(f) e a Im(f) são respectivamente:
Se Comprar 48 livros pagarei uma quantia maior que se comprar 49 livros.
Comprando 20 livros pagarei 50% do valor que equivale a comprar 40 livros.
Comprando 30 livros pagarei um quantia de 340.
Comprar 24 livros é mais barato que comprar 25.
Comprando 20 livros pagarei um quantia de 284.
O domínio e a imagem de uma função definida em várias sentenças, é a união dos domínios e das imagens das sentenças.
Considere a função f(x) e seu esboço gráfico:

O domínio D(f) e a Im(f) são respectivamente: