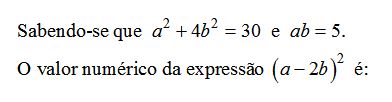MATEMÁTICA I
Simplifique a expressão






Dada a parábola de equação  , pode se dizer que as coordenadas do vértices e o conjunto imagem são respectivamente:
, pode se dizer que as coordenadas do vértices e o conjunto imagem são respectivamente:
%7D) e
e ![Im=]-oo,2]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B2%7D%7B%5C%5D%7D)
%7D) e
e 
%7D) e
e 
%7D) e
e 
%7D) e
e ![Im=]-oo,-4]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B4%7D%7B%5C%5D%7D)
A razão entre o número de meninos e meninas de uma sala de aula é de 3/2. Qual é o percentual de meninos na classe?
50%
60%
45%
30%
40%
Sejam as funções onde A = { 2; 3; 4 } e f( x) = x + 1 , calculando o conjunto imagem de f podemos concluir que:
I. O conjunto imagem é formado por B = {3; 4; 5 }.
II. O conjunto imagem é formado por A = {2; 3; 4 }.
III. O conjunto A = { 2; 3; 4 } representa o domínio dessa função.
E correto que se afirma em:
Apenas III
Apenas em I e III
I, II e III
Apenas II e III
Apenas I e II
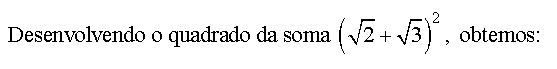
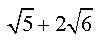
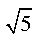
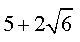
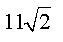
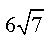
Considere que uma bola é lançada de um canhão e descreve uma trajetória de uma parábola sendo a equação  .
.
Sendo x e y medidos em metros, determine a altura máxima atingida pela bola e o alcance do disparo.
Altura máxima atingida é 40 metros e alcance igual a 4 metros.
Altura máxima atingida é 40 metros e alcance igual a 8 metros.
Altura máxima atingida é 10 metros e alcance igual a 6 metros.
Altura máxima atingida é 20 metros e alcance igual a 4 metros.
Altura máxima atingida é 20 metros e alcance igual a 8 metros.
Se x é um número real tal que %7D%3D%7B9%7D) .
.
Então, o valor de  será igual a:
será igual a:
Dada a parábola de equação  , pode se dizer que as coordenadas do vértices e o conjunto imagem são respectivamente:
, pode se dizer que as coordenadas do vértices e o conjunto imagem são respectivamente:
%7D) e
e ![Im=]-oo,2]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C%7B2%7D%7B%5C%5D%7D)
%7D) e
e 
%7D) e
e 
%7D) e
e 
%7D) e
e ![Im=]-oo,-4]](/tinyMCE3.4.4/cgi-bin/mimetex.cgi?%5Cdisplaystyle%7BI%7D%7Bm%7D%3D%7B%5C%5D%7D-%5Cinfty%2C-%7B4%7D%7B%5C%5D%7D)
A razão entre o número de meninos e meninas de uma sala de aula é de 3/2. Qual é o percentual de meninos na classe?
50%
60%
45%
30%
40%
Sejam as funções onde A = { 2; 3; 4 } e f( x) = x + 1 , calculando o conjunto imagem de f podemos concluir que:
I. O conjunto imagem é formado por B = {3; 4; 5 }.
II. O conjunto imagem é formado por A = {2; 3; 4 }.
III. O conjunto A = { 2; 3; 4 } representa o domínio dessa função.
E correto que se afirma em:
Apenas III
Apenas em I e III
I, II e III
Apenas II e III
Apenas I e II
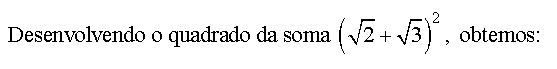
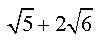
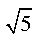
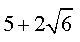
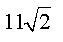
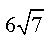
Considere que uma bola é lançada de um canhão e descreve uma trajetória de uma parábola sendo a equação  .
.
Sendo x e y medidos em metros, determine a altura máxima atingida pela bola e o alcance do disparo.
Altura máxima atingida é 40 metros e alcance igual a 4 metros.
Altura máxima atingida é 40 metros e alcance igual a 8 metros.
Altura máxima atingida é 10 metros e alcance igual a 6 metros.
Altura máxima atingida é 20 metros e alcance igual a 4 metros.
Altura máxima atingida é 20 metros e alcance igual a 8 metros.
Se x é um número real tal que %7D%3D%7B9%7D) .
.
Então, o valor de  será igual a:
será igual a:
A razão entre o número de meninos e meninas de uma sala de aula é de 3/2. Qual é o percentual de meninos na classe?
50%
60%
45%
30%
40%
Sejam as funções onde A = { 2; 3; 4 } e f( x) = x + 1 , calculando o conjunto imagem de f podemos concluir que:
I. O conjunto imagem é formado por B = {3; 4; 5 }.
II. O conjunto imagem é formado por A = {2; 3; 4 }.
III. O conjunto A = { 2; 3; 4 } representa o domínio dessa função.
E correto que se afirma em:
Apenas III
Apenas em I e III
I, II e III
Apenas II e III
Apenas I e II
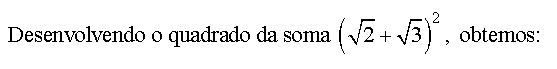
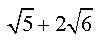
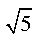
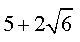
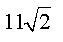
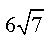
Considere que uma bola é lançada de um canhão e descreve uma trajetória de uma parábola sendo a equação  .
.
Sendo x e y medidos em metros, determine a altura máxima atingida pela bola e o alcance do disparo.
Altura máxima atingida é 40 metros e alcance igual a 4 metros.
Altura máxima atingida é 40 metros e alcance igual a 8 metros.
Altura máxima atingida é 10 metros e alcance igual a 6 metros.
Altura máxima atingida é 20 metros e alcance igual a 4 metros.
Altura máxima atingida é 20 metros e alcance igual a 8 metros.
Se x é um número real tal que %7D%3D%7B9%7D) .
.
Então, o valor de  será igual a:
será igual a:
50%
60%
45%
30%
40%
Sejam as funções onde A = { 2; 3; 4 } e f( x) = x + 1 , calculando o conjunto imagem de f podemos concluir que:
I. O conjunto imagem é formado por B = {3; 4; 5 }.
II. O conjunto imagem é formado por A = {2; 3; 4 }.
III. O conjunto A = { 2; 3; 4 } representa o domínio dessa função.
E correto que se afirma em:
Apenas III
Apenas em I e III
I, II e III
Apenas II e III
Apenas I e II
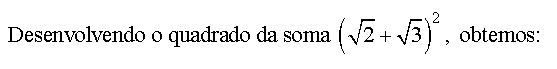
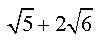
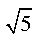
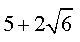
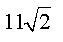
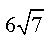
Considere que uma bola é lançada de um canhão e descreve uma trajetória de uma parábola sendo a equação  .
.
Sendo x e y medidos em metros, determine a altura máxima atingida pela bola e o alcance do disparo.
Altura máxima atingida é 40 metros e alcance igual a 4 metros.
Altura máxima atingida é 40 metros e alcance igual a 8 metros.
Altura máxima atingida é 10 metros e alcance igual a 6 metros.
Altura máxima atingida é 20 metros e alcance igual a 4 metros.
Altura máxima atingida é 20 metros e alcance igual a 8 metros.
Se x é um número real tal que %7D%3D%7B9%7D) .
.
Então, o valor de  será igual a:
será igual a:
Apenas III
Apenas em I e III
I, II e III
Apenas II e III
Apenas I e II
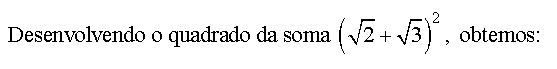
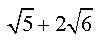
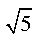
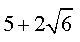
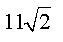
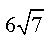
Considere que uma bola é lançada de um canhão e descreve uma trajetória de uma parábola sendo a equação  .
.
Sendo x e y medidos em metros, determine a altura máxima atingida pela bola e o alcance do disparo.
Altura máxima atingida é 40 metros e alcance igual a 4 metros.
Altura máxima atingida é 40 metros e alcance igual a 8 metros.
Altura máxima atingida é 10 metros e alcance igual a 6 metros.
Altura máxima atingida é 20 metros e alcance igual a 4 metros.
Altura máxima atingida é 20 metros e alcance igual a 8 metros.
Se x é um número real tal que %7D%3D%7B9%7D) .
.
Então, o valor de  será igual a:
será igual a:
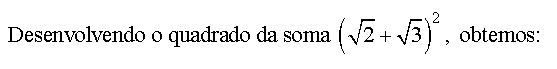
Considere que uma bola é lançada de um canhão e descreve uma trajetória de uma parábola sendo a equação  .
.
Sendo x e y medidos em metros, determine a altura máxima atingida pela bola e o alcance do disparo.
Altura máxima atingida é 40 metros e alcance igual a 4 metros.
Altura máxima atingida é 40 metros e alcance igual a 8 metros.
Altura máxima atingida é 10 metros e alcance igual a 6 metros.
Altura máxima atingida é 20 metros e alcance igual a 4 metros.
Altura máxima atingida é 20 metros e alcance igual a 8 metros.
Se x é um número real tal que %7D%3D%7B9%7D) .
.
Então, o valor de  será igual a:
será igual a:
Altura máxima atingida é 40 metros e alcance igual a 4 metros.
Altura máxima atingida é 40 metros e alcance igual a 8 metros.
Altura máxima atingida é 10 metros e alcance igual a 6 metros.
Altura máxima atingida é 20 metros e alcance igual a 4 metros.
Altura máxima atingida é 20 metros e alcance igual a 8 metros.