MÉTODOS QUANTITATIVOS
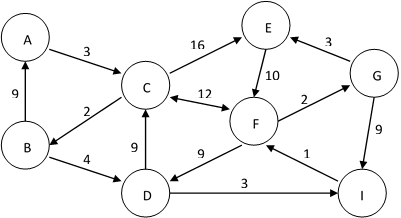
Observando a rede, determinar o menor caminho de A para G:

45
21
39
35
27
Observando a rede, determinar o menor caminho de G para B:
24
26
12
30
18
Considere o seguinte problema de programação linear, onde:
- X1 = produção da peça 1
- X2 = produção da peça 2
- Função objetivo: Max Z = 1900X1 + 2100X2
Sujeito a:
- 100X1 + 200X2 ≤ 500
- 4X1 + 2X2 ≤ 20
- 2X1 + 3X2 ≤ 10
- X1≥ 0 e X2≥ 0
É correto dizer:
Esse sistema não possui soluções viáveis
É impossível produzir 3 peças X1 e 2 peças X2
Esse problema tem várias soluções ótimas
É possível produzir 3 peças X1 e 2 peças X2
Produzir 1 peça X1 e 1 peça X2 é uma solução inviável
As modelagens matemáticas são de suma importância para o auxílio do processo de tomada de decisão. Julgue as sentenças abaixo em Verdadeiro (V) ou Falso (F):
I) Para tomarmos decisões de consequências difíceis
II) Para conhecer os processos
III) Para modificar algo que precisa ser modificado
IV) Para levantar custos
V) Para definir metas de produção
Assinale a sequência correta:
F - V - V - V - F
F - F - F - F - V
V - V - F - V - F
V - F - F - F - F
V - F - F - V - F
Observando a rede, determinar o menor caminho de A para I:

14
19
12
24
08
Abaixo estão apresentadas, fora de ordem, as cinco fases num projeto de resolução de problemas:
I) Obtenção da solução
II) Teste do modelo e avaliação da solução
III) Formulação do problema
IV) Implantação e acompanhamento da solução (manutenção)
V) Construção do modelo
Classifique-as corretamente e, em seguida, marque a alternativa que contém a sequência correta das fases:
3 - 5 - 1 - 2 - 4
3 - 5 - 2 - 1 - 4
4 - 5 - 1 - 2 - 3
1 - 2 - 3 - 4 - 5
3 - 2 - 1 - 5 - 4
Dado o seguinte problema de programação linear:
- maxZ = 16X1 + 6X2 + 15X3
- 10x1 + 3x2 + 2x3 ≤ 1200
- 5x1 + 2x2 + 5x3 ≤ 2000
- x1, x2, x3 ≥ 0
Podemos admitir que é Verdadeira a afirmativa:
A solução X1≥10, X2≥100, X3≥300 é uma solução viável
A solução X1=10, X2=100, X3=300 é uma solução viável
A solução X1≥10, X2=1000, X3=3000 é uma solução viável
A solução X1=100, X2=100, X3=300 é uma solução viável
A solução X1≤10, X2=100, X3≥300 é uma solução viável
Os modelos, como representações de situações reais, são úteis para auxiliar o processo de tomada de decisão. Segundo LACHTERMACHER, há três tipos de modelos: os modelos físicos, os modelos análogos e os modelos matemáticos ou simbólicos. Considerando as características dos modelos, julgue as seguintes afirmações:
I) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo análogo.
II) O projeto arquitetônico de uma residência de 100 m², projeto esse composto por um conjunto de desenhos de arquitetura, é um modelo simbólico.
III) As equações e, em que: demanda por residências de 100 m² no ano de 2017 em Araraquara-SP, preço médio de uma residência de 100 m² no ano de 2017 em Araraquara-SP; oferta de residências de 100 m² no ano de 2017 em Uberaba, são parâmetros, representam um modelo simbólico.
IV) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo físico.
Estão corretas apenas as afirmações:

45
21
39
35
27
Observando a rede, determinar o menor caminho de G para B:

24
26
12
30
18
Considere o seguinte problema de programação linear, onde:
- X1 = produção da peça 1
- X2 = produção da peça 2
- Função objetivo: Max Z = 1900X1 + 2100X2
Sujeito a:
- 100X1 + 200X2 ≤ 500
- 4X1 + 2X2 ≤ 20
- 2X1 + 3X2 ≤ 10
- X1≥ 0 e X2≥ 0
É correto dizer:
Esse sistema não possui soluções viáveis
É impossível produzir 3 peças X1 e 2 peças X2
Esse problema tem várias soluções ótimas
É possível produzir 3 peças X1 e 2 peças X2
Produzir 1 peça X1 e 1 peça X2 é uma solução inviável
As modelagens matemáticas são de suma importância para o auxílio do processo de tomada de decisão. Julgue as sentenças abaixo em Verdadeiro (V) ou Falso (F):
I) Para tomarmos decisões de consequências difíceis
II) Para conhecer os processos
III) Para modificar algo que precisa ser modificado
IV) Para levantar custos
V) Para definir metas de produção
Assinale a sequência correta:
F - V - V - V - F
F - F - F - F - V
V - V - F - V - F
V - F - F - F - F
V - F - F - V - F
Observando a rede, determinar o menor caminho de A para I:

14
19
12
24
08
Abaixo estão apresentadas, fora de ordem, as cinco fases num projeto de resolução de problemas:
I) Obtenção da solução
II) Teste do modelo e avaliação da solução
III) Formulação do problema
IV) Implantação e acompanhamento da solução (manutenção)
V) Construção do modelo
Classifique-as corretamente e, em seguida, marque a alternativa que contém a sequência correta das fases:
3 - 5 - 1 - 2 - 4
3 - 5 - 2 - 1 - 4
4 - 5 - 1 - 2 - 3
1 - 2 - 3 - 4 - 5
3 - 2 - 1 - 5 - 4
Dado o seguinte problema de programação linear:
- maxZ = 16X1 + 6X2 + 15X3
- 10x1 + 3x2 + 2x3 ≤ 1200
- 5x1 + 2x2 + 5x3 ≤ 2000
- x1, x2, x3 ≥ 0
Podemos admitir que é Verdadeira a afirmativa:
A solução X1≥10, X2≥100, X3≥300 é uma solução viável
A solução X1=10, X2=100, X3=300 é uma solução viável
A solução X1≥10, X2=1000, X3=3000 é uma solução viável
A solução X1=100, X2=100, X3=300 é uma solução viável
A solução X1≤10, X2=100, X3≥300 é uma solução viável
Os modelos, como representações de situações reais, são úteis para auxiliar o processo de tomada de decisão. Segundo LACHTERMACHER, há três tipos de modelos: os modelos físicos, os modelos análogos e os modelos matemáticos ou simbólicos. Considerando as características dos modelos, julgue as seguintes afirmações:
I) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo análogo.
II) O projeto arquitetônico de uma residência de 100 m², projeto esse composto por um conjunto de desenhos de arquitetura, é um modelo simbólico.
III) As equações e, em que: demanda por residências de 100 m² no ano de 2017 em Araraquara-SP, preço médio de uma residência de 100 m² no ano de 2017 em Araraquara-SP; oferta de residências de 100 m² no ano de 2017 em Uberaba, são parâmetros, representam um modelo simbólico.
IV) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo físico.
Estão corretas apenas as afirmações:

24
26
12
30
18
Considere o seguinte problema de programação linear, onde:
- X1 = produção da peça 1
- X2 = produção da peça 2
- Função objetivo: Max Z = 1900X1 + 2100X2
Sujeito a:
- 100X1 + 200X2 ≤ 500
- 4X1 + 2X2 ≤ 20
- 2X1 + 3X2 ≤ 10
- X1≥ 0 e X2≥ 0
É correto dizer:
Esse sistema não possui soluções viáveis
É impossível produzir 3 peças X1 e 2 peças X2
Esse problema tem várias soluções ótimas
É possível produzir 3 peças X1 e 2 peças X2
Produzir 1 peça X1 e 1 peça X2 é uma solução inviável
As modelagens matemáticas são de suma importância para o auxílio do processo de tomada de decisão. Julgue as sentenças abaixo em Verdadeiro (V) ou Falso (F):
I) Para tomarmos decisões de consequências difíceis
II) Para conhecer os processos
III) Para modificar algo que precisa ser modificado
IV) Para levantar custos
V) Para definir metas de produção
Assinale a sequência correta:
F - V - V - V - F
F - F - F - F - V
V - V - F - V - F
V - F - F - F - F
V - F - F - V - F
Observando a rede, determinar o menor caminho de A para I:

14
19
12
24
08
Abaixo estão apresentadas, fora de ordem, as cinco fases num projeto de resolução de problemas:
I) Obtenção da solução
II) Teste do modelo e avaliação da solução
III) Formulação do problema
IV) Implantação e acompanhamento da solução (manutenção)
V) Construção do modelo
Classifique-as corretamente e, em seguida, marque a alternativa que contém a sequência correta das fases:
3 - 5 - 1 - 2 - 4
3 - 5 - 2 - 1 - 4
4 - 5 - 1 - 2 - 3
1 - 2 - 3 - 4 - 5
3 - 2 - 1 - 5 - 4
Dado o seguinte problema de programação linear:
- maxZ = 16X1 + 6X2 + 15X3
- 10x1 + 3x2 + 2x3 ≤ 1200
- 5x1 + 2x2 + 5x3 ≤ 2000
- x1, x2, x3 ≥ 0
Podemos admitir que é Verdadeira a afirmativa:
A solução X1≥10, X2≥100, X3≥300 é uma solução viável
A solução X1=10, X2=100, X3=300 é uma solução viável
A solução X1≥10, X2=1000, X3=3000 é uma solução viável
A solução X1=100, X2=100, X3=300 é uma solução viável
A solução X1≤10, X2=100, X3≥300 é uma solução viável
Os modelos, como representações de situações reais, são úteis para auxiliar o processo de tomada de decisão. Segundo LACHTERMACHER, há três tipos de modelos: os modelos físicos, os modelos análogos e os modelos matemáticos ou simbólicos. Considerando as características dos modelos, julgue as seguintes afirmações:
I) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo análogo.
II) O projeto arquitetônico de uma residência de 100 m², projeto esse composto por um conjunto de desenhos de arquitetura, é um modelo simbólico.
III) As equações e, em que: demanda por residências de 100 m² no ano de 2017 em Araraquara-SP, preço médio de uma residência de 100 m² no ano de 2017 em Araraquara-SP; oferta de residências de 100 m² no ano de 2017 em Uberaba, são parâmetros, representam um modelo simbólico.
IV) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo físico.
Estão corretas apenas as afirmações:
Esse sistema não possui soluções viáveis
É impossível produzir 3 peças X1 e 2 peças X2
Esse problema tem várias soluções ótimas
É possível produzir 3 peças X1 e 2 peças X2
Produzir 1 peça X1 e 1 peça X2 é uma solução inviável
As modelagens matemáticas são de suma importância para o auxílio do processo de tomada de decisão. Julgue as sentenças abaixo em Verdadeiro (V) ou Falso (F):
I) Para tomarmos decisões de consequências difíceis
II) Para conhecer os processos
III) Para modificar algo que precisa ser modificado
IV) Para levantar custos
V) Para definir metas de produção
Assinale a sequência correta:
F - V - V - V - F
F - F - F - F - V
V - V - F - V - F
V - F - F - F - F
V - F - F - V - F
Observando a rede, determinar o menor caminho de A para I:

14
19
12
24
08
Abaixo estão apresentadas, fora de ordem, as cinco fases num projeto de resolução de problemas:
I) Obtenção da solução
II) Teste do modelo e avaliação da solução
III) Formulação do problema
IV) Implantação e acompanhamento da solução (manutenção)
V) Construção do modelo
Classifique-as corretamente e, em seguida, marque a alternativa que contém a sequência correta das fases:
3 - 5 - 1 - 2 - 4
3 - 5 - 2 - 1 - 4
4 - 5 - 1 - 2 - 3
1 - 2 - 3 - 4 - 5
3 - 2 - 1 - 5 - 4
Dado o seguinte problema de programação linear:
- maxZ = 16X1 + 6X2 + 15X3
- 10x1 + 3x2 + 2x3 ≤ 1200
- 5x1 + 2x2 + 5x3 ≤ 2000
- x1, x2, x3 ≥ 0
Podemos admitir que é Verdadeira a afirmativa:
A solução X1≥10, X2≥100, X3≥300 é uma solução viável
A solução X1=10, X2=100, X3=300 é uma solução viável
A solução X1≥10, X2=1000, X3=3000 é uma solução viável
A solução X1=100, X2=100, X3=300 é uma solução viável
A solução X1≤10, X2=100, X3≥300 é uma solução viável
Os modelos, como representações de situações reais, são úteis para auxiliar o processo de tomada de decisão. Segundo LACHTERMACHER, há três tipos de modelos: os modelos físicos, os modelos análogos e os modelos matemáticos ou simbólicos. Considerando as características dos modelos, julgue as seguintes afirmações:
I) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo análogo.
II) O projeto arquitetônico de uma residência de 100 m², projeto esse composto por um conjunto de desenhos de arquitetura, é um modelo simbólico.
III) As equações e, em que: demanda por residências de 100 m² no ano de 2017 em Araraquara-SP, preço médio de uma residência de 100 m² no ano de 2017 em Araraquara-SP; oferta de residências de 100 m² no ano de 2017 em Uberaba, são parâmetros, representam um modelo simbólico.
IV) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo físico.
Estão corretas apenas as afirmações:
F - V - V - V - F
F - F - F - F - V
V - V - F - V - F
V - F - F - F - F
V - F - F - V - F
Observando a rede, determinar o menor caminho de A para I:

14
19
12
24
08
Abaixo estão apresentadas, fora de ordem, as cinco fases num projeto de resolução de problemas:
I) Obtenção da solução
II) Teste do modelo e avaliação da solução
III) Formulação do problema
IV) Implantação e acompanhamento da solução (manutenção)
V) Construção do modelo
Classifique-as corretamente e, em seguida, marque a alternativa que contém a sequência correta das fases:
3 - 5 - 1 - 2 - 4
3 - 5 - 2 - 1 - 4
4 - 5 - 1 - 2 - 3
1 - 2 - 3 - 4 - 5
3 - 2 - 1 - 5 - 4
Dado o seguinte problema de programação linear:
- maxZ = 16X1 + 6X2 + 15X3
- 10x1 + 3x2 + 2x3 ≤ 1200
- 5x1 + 2x2 + 5x3 ≤ 2000
- x1, x2, x3 ≥ 0
Podemos admitir que é Verdadeira a afirmativa:
A solução X1≥10, X2≥100, X3≥300 é uma solução viável
A solução X1=10, X2=100, X3=300 é uma solução viável
A solução X1≥10, X2=1000, X3=3000 é uma solução viável
A solução X1=100, X2=100, X3=300 é uma solução viável
A solução X1≤10, X2=100, X3≥300 é uma solução viável
Os modelos, como representações de situações reais, são úteis para auxiliar o processo de tomada de decisão. Segundo LACHTERMACHER, há três tipos de modelos: os modelos físicos, os modelos análogos e os modelos matemáticos ou simbólicos. Considerando as características dos modelos, julgue as seguintes afirmações:
I) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo análogo.
II) O projeto arquitetônico de uma residência de 100 m², projeto esse composto por um conjunto de desenhos de arquitetura, é um modelo simbólico.
III) As equações e, em que: demanda por residências de 100 m² no ano de 2017 em Araraquara-SP, preço médio de uma residência de 100 m² no ano de 2017 em Araraquara-SP; oferta de residências de 100 m² no ano de 2017 em Uberaba, são parâmetros, representam um modelo simbólico.
IV) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo físico.
Estão corretas apenas as afirmações:

14
19
12
24
08
Abaixo estão apresentadas, fora de ordem, as cinco fases num projeto de resolução de problemas:
I) Obtenção da solução
II) Teste do modelo e avaliação da solução
III) Formulação do problema
IV) Implantação e acompanhamento da solução (manutenção)
V) Construção do modelo
Classifique-as corretamente e, em seguida, marque a alternativa que contém a sequência correta das fases:
3 - 5 - 1 - 2 - 4
3 - 5 - 2 - 1 - 4
4 - 5 - 1 - 2 - 3
1 - 2 - 3 - 4 - 5
3 - 2 - 1 - 5 - 4
Dado o seguinte problema de programação linear:
- maxZ = 16X1 + 6X2 + 15X3
- 10x1 + 3x2 + 2x3 ≤ 1200
- 5x1 + 2x2 + 5x3 ≤ 2000
- x1, x2, x3 ≥ 0
Podemos admitir que é Verdadeira a afirmativa:
A solução X1≥10, X2≥100, X3≥300 é uma solução viável
A solução X1=10, X2=100, X3=300 é uma solução viável
A solução X1≥10, X2=1000, X3=3000 é uma solução viável
A solução X1=100, X2=100, X3=300 é uma solução viável
A solução X1≤10, X2=100, X3≥300 é uma solução viável
Os modelos, como representações de situações reais, são úteis para auxiliar o processo de tomada de decisão. Segundo LACHTERMACHER, há três tipos de modelos: os modelos físicos, os modelos análogos e os modelos matemáticos ou simbólicos. Considerando as características dos modelos, julgue as seguintes afirmações:
I) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo análogo.
II) O projeto arquitetônico de uma residência de 100 m², projeto esse composto por um conjunto de desenhos de arquitetura, é um modelo simbólico.
III) As equações e, em que: demanda por residências de 100 m² no ano de 2017 em Araraquara-SP, preço médio de uma residência de 100 m² no ano de 2017 em Araraquara-SP; oferta de residências de 100 m² no ano de 2017 em Uberaba, são parâmetros, representam um modelo simbólico.
IV) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo físico.
Estão corretas apenas as afirmações:
3 - 5 - 1 - 2 - 4
3 - 5 - 2 - 1 - 4
4 - 5 - 1 - 2 - 3
1 - 2 - 3 - 4 - 5
3 - 2 - 1 - 5 - 4
Dado o seguinte problema de programação linear:
- maxZ = 16X1 + 6X2 + 15X3
- 10x1 + 3x2 + 2x3 ≤ 1200
- 5x1 + 2x2 + 5x3 ≤ 2000
- x1, x2, x3 ≥ 0
Podemos admitir que é Verdadeira a afirmativa:
A solução X1≥10, X2≥100, X3≥300 é uma solução viável
A solução X1=10, X2=100, X3=300 é uma solução viável
A solução X1≥10, X2=1000, X3=3000 é uma solução viável
A solução X1=100, X2=100, X3=300 é uma solução viável
A solução X1≤10, X2=100, X3≥300 é uma solução viável
Os modelos, como representações de situações reais, são úteis para auxiliar o processo de tomada de decisão. Segundo LACHTERMACHER, há três tipos de modelos: os modelos físicos, os modelos análogos e os modelos matemáticos ou simbólicos. Considerando as características dos modelos, julgue as seguintes afirmações:
I) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo análogo.
II) O projeto arquitetônico de uma residência de 100 m², projeto esse composto por um conjunto de desenhos de arquitetura, é um modelo simbólico.
III) As equações e, em que: demanda por residências de 100 m² no ano de 2017 em Araraquara-SP, preço médio de uma residência de 100 m² no ano de 2017 em Araraquara-SP; oferta de residências de 100 m² no ano de 2017 em Uberaba, são parâmetros, representam um modelo simbólico.
IV) A maquete de residências de 100 m² a serem construídas no bairro Vila Xavier, em Araraquara-SP, no ano de 2017, é um modelo físico.
Estão corretas apenas as afirmações:
A solução X1≥10, X2≥100, X3≥300 é uma solução viável
A solução X1=10, X2=100, X3=300 é uma solução viável
A solução X1≥10, X2=1000, X3=3000 é uma solução viável
A solução X1=100, X2=100, X3=300 é uma solução viável
A solução X1≤10, X2=100, X3≥300 é uma solução viável