GEOMETRIA ANALÍTICA
Encontre uma equação para parábola de vértice V(3, -2), eixo paralelo ao dos y e parâmetro p = 1.
(x - 2)2 = 2(y + 3)
(y - 3)2 = 2(x + 2)
(y + 3)2 = 2(x - 2)
(x - 3)2 = 2(y + 2)
(x + 3)2 = 2(y - 2)
A equação da vetorial da reta que é a interseção dos planos II para I 
r: (x,y,z) = (-3,2,1) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(-1,1,3)
r: (x,y,z) = (3,2,0) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(1,1,1)
Dados os vetores a=(2,-1,1), b=(1,-1,0) e c=(x,1,-3) assinale a alternativa que contém o(s) valor(es) de x, para que o volume do paralelepípedo definido pelos vetores a, b e c seja igual a 1?
x=2
x=6 ou x=-3
x=-5 ou x=-3
x=5
x=5 ou x=3
Qual das alternativas abaixo representa o versor de V = (3, -4)?
%7D "((3)/(5),(-4)/(5))")
%7D "((3)/(5),(4)/(5))")
%7D "((5)/(3),(-4)/(3))")
%7D "((-3)/(5),(-4)/(5))")
%7D "((-3)/(5),(4)/(5))")
Sabendo que |u| = 4 e |v| = 2, cujo ângulo entre eles é 120°, encontre o valor do módulo de u + v.
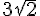
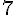
Sejam ar , as e at , respectivamente, as inclinações das retas r, s, e t representadas na figura, a seguir.
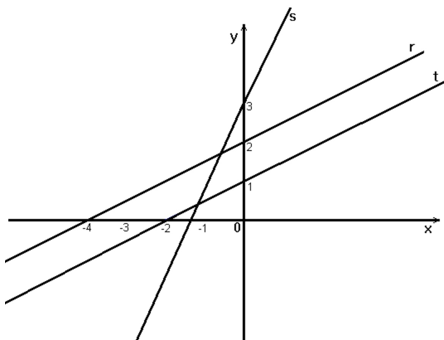
É correto o que se afirma em
as < ar = at
ar = at < as
ar = at = as
as < ar < at
ar < at < as
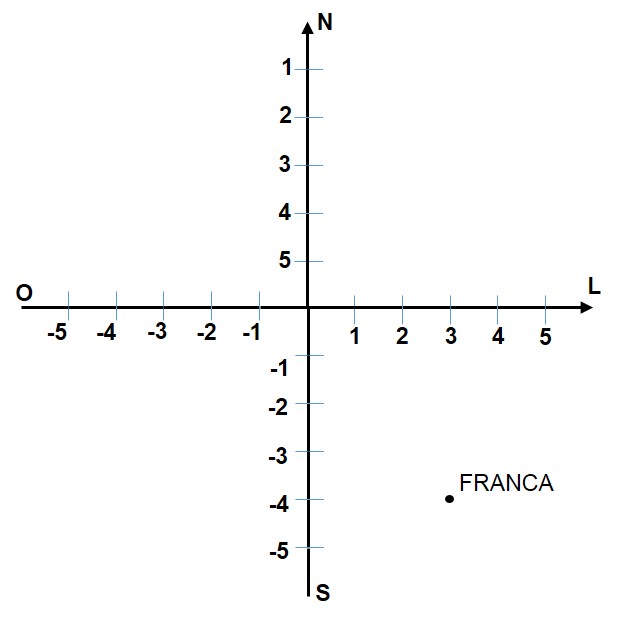
José e sua família estão planejando suas férias. Eles moram em Franca, São Paulo, e pretendem visitar Anápolis, Goiás, passando antes por Uberaba, Minas Gerais. Considerando uma representação dessas três cidades em um plano cartesiano, tendo Franca no ponto (3, 4), as localizações das outras cidades serão assim definidas: para ir de Franca a Uberaba eles irão percorrer três unidades de medida no sentido Oeste e quatro no sentido Norte. Após o passeio em Uberaba, José irá dirigir cinco unidades de medida no sentido Norte e mais duas no sentido Oeste, pois é o caminho que ele considera mais perto para chegar a Anápolis. Considerando a opção de José, em que ponto do plano Anápolis está localizada?
(5, 2)
(2, 5)
(2, 5)
(5, 2)
(0, 0)
Calcule o ângulo entre as retas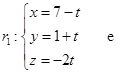 
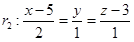e assinale a alternativa correspondente.
90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por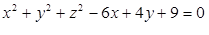 
. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use 
= 3,14.
(x - 2)2 = 2(y + 3)
(y - 3)2 = 2(x + 2)
(y + 3)2 = 2(x - 2)
(x - 3)2 = 2(y + 2)
(x + 3)2 = 2(y - 2)
A equação da vetorial da reta que é a interseção dos planos II para I
r: (x,y,z) = (-3,2,1) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(-1,1,3)
r: (x,y,z) = (3,2,0) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(1,1,1)
Dados os vetores a=(2,-1,1), b=(1,-1,0) e c=(x,1,-3) assinale a alternativa que contém o(s) valor(es) de x, para que o volume do paralelepípedo definido pelos vetores a, b e c seja igual a 1?
x=2
x=6 ou x=-3
x=-5 ou x=-3
x=5
x=5 ou x=3
Qual das alternativas abaixo representa o versor de V = (3, -4)?
Sabendo que |u| = 4 e |v| = 2, cujo ângulo entre eles é 120°, encontre o valor do módulo de u + v.
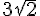
Sejam ar , as e at , respectivamente, as inclinações das retas r, s, e t representadas na figura, a seguir.
É correto o que se afirma em
as < ar = at
ar = at < as
ar = at = as
as < ar < at
ar < at < as
José e sua família estão planejando suas férias. Eles moram em Franca, São Paulo, e pretendem visitar Anápolis, Goiás, passando antes por Uberaba, Minas Gerais. Considerando uma representação dessas três cidades em um plano cartesiano, tendo Franca no ponto (3, 4), as localizações das outras cidades serão assim definidas: para ir de Franca a Uberaba eles irão percorrer três unidades de medida no sentido Oeste e quatro no sentido Norte. Após o passeio em Uberaba, José irá dirigir cinco unidades de medida no sentido Norte e mais duas no sentido Oeste, pois é o caminho que ele considera mais perto para chegar a Anápolis. Considerando a opção de José, em que ponto do plano Anápolis está localizada?
(5, 2)
(2, 5)
(2, 5)
(5, 2)
(0, 0)
Calcule o ângulo entre as retas 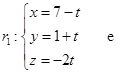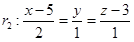e assinale a alternativa correspondente.
90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por 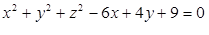. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use = 3,14.
r: (x,y,z) = (-3,2,1) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(-1,1,3)
r: (x,y,z) = (3,2,0) + t(-1,1,1)
r: (x,y,z) = (-3,2,0) + t(1,1,1)
Dados os vetores a=(2,-1,1), b=(1,-1,0) e c=(x,1,-3) assinale a alternativa que contém o(s) valor(es) de x, para que o volume do paralelepípedo definido pelos vetores a, b e c seja igual a 1?
x=2
x=6 ou x=-3
x=-5 ou x=-3
x=5
x=5 ou x=3
Qual das alternativas abaixo representa o versor de V = (3, -4)?
Sabendo que |u| = 4 e |v| = 2, cujo ângulo entre eles é 120°, encontre o valor do módulo de u + v.
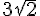
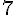
Sejam ar , as e at , respectivamente, as inclinações das retas r, s, e t representadas na figura, a seguir.
É correto o que se afirma em
as < ar = at
ar = at < as
ar = at = as
as < ar < at
ar < at < as
José e sua família estão planejando suas férias. Eles moram em Franca, São Paulo, e pretendem visitar Anápolis, Goiás, passando antes por Uberaba, Minas Gerais. Considerando uma representação dessas três cidades em um plano cartesiano, tendo Franca no ponto (3, 4), as localizações das outras cidades serão assim definidas: para ir de Franca a Uberaba eles irão percorrer três unidades de medida no sentido Oeste e quatro no sentido Norte. Após o passeio em Uberaba, José irá dirigir cinco unidades de medida no sentido Norte e mais duas no sentido Oeste, pois é o caminho que ele considera mais perto para chegar a Anápolis. Considerando a opção de José, em que ponto do plano Anápolis está localizada?
(5, 2)
(2, 5)
(2, 5)
(5, 2)
(0, 0)
Calcule o ângulo entre as retas 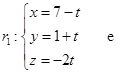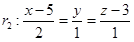e assinale a alternativa correspondente.
90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por 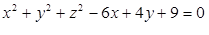. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use = 3,14.
x=2
x=6 ou x=-3
x=-5 ou x=-3
x=5
x=5 ou x=3
Qual das alternativas abaixo representa o versor de V = (3, -4)?
Sabendo que |u| = 4 e |v| = 2, cujo ângulo entre eles é 120°, encontre o valor do módulo de u + v.
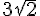
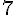
Sejam ar , as e at , respectivamente, as inclinações das retas r, s, e t representadas na figura, a seguir.
É correto o que se afirma em
as < ar = at
ar = at < as
ar = at = as
as < ar < at
ar < at < as
José e sua família estão planejando suas férias. Eles moram em Franca, São Paulo, e pretendem visitar Anápolis, Goiás, passando antes por Uberaba, Minas Gerais. Considerando uma representação dessas três cidades em um plano cartesiano, tendo Franca no ponto (3, 4), as localizações das outras cidades serão assim definidas: para ir de Franca a Uberaba eles irão percorrer três unidades de medida no sentido Oeste e quatro no sentido Norte. Após o passeio em Uberaba, José irá dirigir cinco unidades de medida no sentido Norte e mais duas no sentido Oeste, pois é o caminho que ele considera mais perto para chegar a Anápolis. Considerando a opção de José, em que ponto do plano Anápolis está localizada?
(5, 2)
(2, 5)
(2, 5)
(5, 2)
(0, 0)
Calcule o ângulo entre as retas 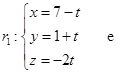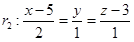e assinale a alternativa correspondente.
90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por 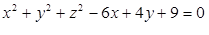. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use = 3,14.
Sabendo que |u| = 4 e |v| = 2, cujo ângulo entre eles é 120°, encontre o valor do módulo de u + v.
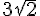
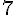
Sejam ar , as e at , respectivamente, as inclinações das retas r, s, e t representadas na figura, a seguir.
É correto o que se afirma em
as < ar = at
ar = at < as
ar = at = as
as < ar < at
ar < at < as
José e sua família estão planejando suas férias. Eles moram em Franca, São Paulo, e pretendem visitar Anápolis, Goiás, passando antes por Uberaba, Minas Gerais. Considerando uma representação dessas três cidades em um plano cartesiano, tendo Franca no ponto (3, 4), as localizações das outras cidades serão assim definidas: para ir de Franca a Uberaba eles irão percorrer três unidades de medida no sentido Oeste e quatro no sentido Norte. Após o passeio em Uberaba, José irá dirigir cinco unidades de medida no sentido Norte e mais duas no sentido Oeste, pois é o caminho que ele considera mais perto para chegar a Anápolis. Considerando a opção de José, em que ponto do plano Anápolis está localizada?
(5, 2)
(2, 5)
(2, 5)
(5, 2)
(0, 0)
Calcule o ângulo entre as retas 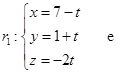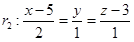e assinale a alternativa correspondente.
90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por 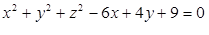. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use = 3,14.
Sejam ar , as e at , respectivamente, as inclinações das retas r, s, e t representadas na figura, a seguir.
É correto o que se afirma em
as < ar = at
ar = at < as
ar = at = as
as < ar < at
ar < at < as
José e sua família estão planejando suas férias. Eles moram em Franca, São Paulo, e pretendem visitar Anápolis, Goiás, passando antes por Uberaba, Minas Gerais. Considerando uma representação dessas três cidades em um plano cartesiano, tendo Franca no ponto (3, 4), as localizações das outras cidades serão assim definidas: para ir de Franca a Uberaba eles irão percorrer três unidades de medida no sentido Oeste e quatro no sentido Norte. Após o passeio em Uberaba, José irá dirigir cinco unidades de medida no sentido Norte e mais duas no sentido Oeste, pois é o caminho que ele considera mais perto para chegar a Anápolis. Considerando a opção de José, em que ponto do plano Anápolis está localizada?
(5, 2)
(2, 5)
(2, 5)
(5, 2)
(0, 0)
Calcule o ângulo entre as retas 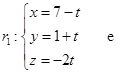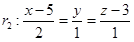e assinale a alternativa correspondente.
90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por 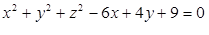. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use = 3,14.
as < ar = at
ar = at < as
ar = at = as
as < ar < at
ar < at < as
José e sua família estão planejando suas férias. Eles moram em Franca, São Paulo, e pretendem visitar Anápolis, Goiás, passando antes por Uberaba, Minas Gerais. Considerando uma representação dessas três cidades em um plano cartesiano, tendo Franca no ponto (3, 4), as localizações das outras cidades serão assim definidas: para ir de Franca a Uberaba eles irão percorrer três unidades de medida no sentido Oeste e quatro no sentido Norte. Após o passeio em Uberaba, José irá dirigir cinco unidades de medida no sentido Norte e mais duas no sentido Oeste, pois é o caminho que ele considera mais perto para chegar a Anápolis. Considerando a opção de José, em que ponto do plano Anápolis está localizada?
(5, 2)
(2, 5)
(2, 5)
(5, 2)
(0, 0)
Calcule o ângulo entre as retas 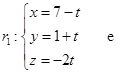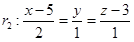e assinale a alternativa correspondente.
90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por 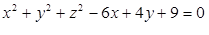. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use = 3,14.
(5, 2)
(2, 5)
(2, 5)
(5, 2)
(0, 0)
Calcule o ângulo entre as retas 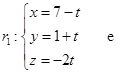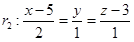e assinale a alternativa correspondente.
90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por 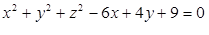. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use = 3,14.
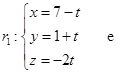
e assinale a alternativa correspondente.90º
65º
70º
60º
45º
Considerando a equação da superfície expressa por 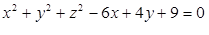. Assinale a alternativa correta.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Considerando que uma esfera tem raio igual a 15 cm assinale a alternativa que expressa o seu volume e sua área, respectivamente. Use = 3,14.
. Assinale a alternativa correta.Refere-se a uma superfície cilíndrica de centro de coordenadas (3, -2, 0) e raio igual a 4.
Refere-se a uma superfície cônica de centro de coordenadas (-3, -2, 0) e raio igual a 4.
Refere-se a uma superfície esférica de centro de coordenadas (3, 2, 0) e raio igual a 2.
Refere-se a uma superfície esférica de centro de coordenadas (3, -2, 0) e raio igual a 2.
Refere-se a uma superfície cilíndrica de centro de coordenadas (3, 2, 0) e raio igual a 2.