GEOMETRIA ANALÍTICA
Considere uma hipérbole com a excentricidade e= e os vértices são A1(2,0) e A2(–2,0). Assinale a alternativa que contém as coordenadas cartesianas do foco desta hipérbole.
e os vértices são A1(2,0) e A2(–2,0). Assinale a alternativa que contém as coordenadas cartesianas do foco desta hipérbole.
%7D%2C%7B%5Cleft(%7B0%7D%2C%7B2%7D%5Csqrt%7B%7B%7B5%7D%7D%7D%5Cright)%7D)
%7D%2C%7B%5Cleft(%7B0%7D%2C%7B2%7D%5Csqrt%7B%7B%7B5%7D%7D%7D%5Cright)%7D)
%7D%2C%7B%5Cleft(%7B2%7D%5Csqrt%7B%7B%7B5%7D%7D%7D%2C%7B0%7D%5Cright)%7D)
%7D%2C%7B%5Cleft(%7B2%7D%5Csqrt%7B%7B%7B5%7D%7D%7D%2C%7B0%7D%5Cright)%7D)
%7D%2C%7B%5Cleft(%7B0%7D%2C%7B0%7D%5Cright)%7D)
Sabendo que o plano  é determinado pelos pontos A(1,-1,2), B(2,1,-3) e C(-1,-2,6), assinale a alternativa que representa a equação geral de
é determinado pelos pontos A(1,-1,2), B(2,1,-3) e C(-1,-2,6), assinale a alternativa que representa a equação geral de  .
.
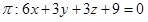
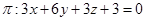
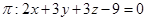
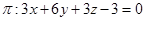
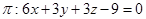
Dados os vetores u = (1, 1, -1) e v = (2, -3, 4) qual a área do paralelogramo determinado por u e v?








O produto escalar entre u e v considerando u=(3,3,3) e v=(-1,-5,4) está corretamente expresso na alternativa
2
-1
4
-6
6
As grandezas físicas são classificadas pelo critério do que é necessário para a sua total compreensão. As escalares exigem o módulo e a unidade de referência e as vetoriais exigem o módulo, a direção e o sentido. Neste sentido, classifique as grandezas em (E) escalar ou (V) vetorial.
( ) . Velocidade
( ) . Temperatura
( ) . Área
( ) . Torque
( ) . Força
É correta a sequência que corresponde a alternativa
V, V,V,E,V.
V, E,E,V,V.
V, E,V,E,V.
V, E,E,V,E.
E, E,E,V,V.
Os vetores podem ser representados, também, por meio dos versores 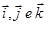 . Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja,
. Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja, 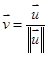 . Baseando-se nessas informações e considerando que
. Baseando-se nessas informações e considerando que pode-se concluir que o versor do vetor formado por
pode-se concluir que o versor do vetor formado por 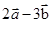 , está corretamente representado na alternativa
, está corretamente representado na alternativa
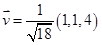
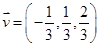
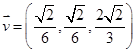

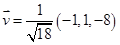
No plano cartesiano, considere os pontos A(-1, 2) e B(3, 4). Encontre a equação da reta r que passa por A e forma com o eixo das abscissas um ângulo de 45°, medido do eixo para a reta no sentido anti-horário.
y = x + 3
y = - x + 1
y = - x - 1
y = x - 1
y = x - 3
Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:
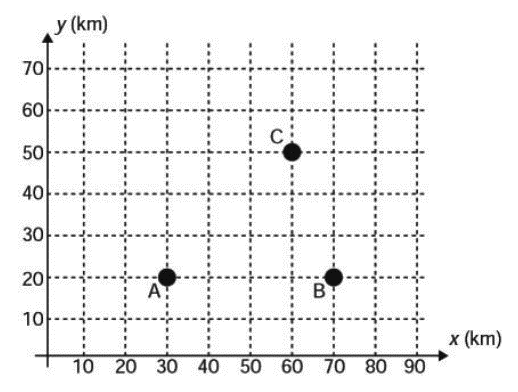
A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
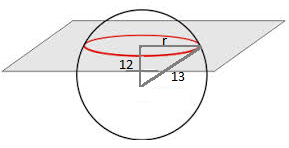
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a
Sabendo que o plano  é determinado pelos pontos A(1,-1,2), B(2,1,-3) e C(-1,-2,6), assinale a alternativa que representa a equação geral de
é determinado pelos pontos A(1,-1,2), B(2,1,-3) e C(-1,-2,6), assinale a alternativa que representa a equação geral de  .
.
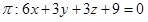
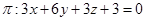
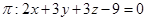
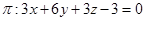
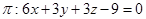
Dados os vetores u = (1, 1, -1) e v = (2, -3, 4) qual a área do paralelogramo determinado por u e v?








O produto escalar entre u e v considerando u=(3,3,3) e v=(-1,-5,4) está corretamente expresso na alternativa
2
-1
4
-6
6
As grandezas físicas são classificadas pelo critério do que é necessário para a sua total compreensão. As escalares exigem o módulo e a unidade de referência e as vetoriais exigem o módulo, a direção e o sentido. Neste sentido, classifique as grandezas em (E) escalar ou (V) vetorial.
( ) . Velocidade
( ) . Temperatura
( ) . Área
( ) . Torque
( ) . Força
É correta a sequência que corresponde a alternativa
V, V,V,E,V.
V, E,E,V,V.
V, E,V,E,V.
V, E,E,V,E.
E, E,E,V,V.
Os vetores podem ser representados, também, por meio dos versores 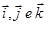 . Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja,
. Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja, 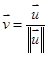 . Baseando-se nessas informações e considerando que
. Baseando-se nessas informações e considerando que pode-se concluir que o versor do vetor formado por
pode-se concluir que o versor do vetor formado por 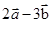 , está corretamente representado na alternativa
, está corretamente representado na alternativa
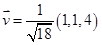
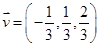
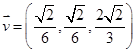

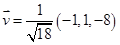
No plano cartesiano, considere os pontos A(-1, 2) e B(3, 4). Encontre a equação da reta r que passa por A e forma com o eixo das abscissas um ângulo de 45°, medido do eixo para a reta no sentido anti-horário.
y = x + 3
y = - x + 1
y = - x - 1
y = x - 1
y = x - 3
Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a

![]()
![]()
![]()
![]()
![]()
Dados os vetores u = (1, 1, -1) e v = (2, -3, 4) qual a área do paralelogramo determinado por u e v?








O produto escalar entre u e v considerando u=(3,3,3) e v=(-1,-5,4) está corretamente expresso na alternativa
2
-1
4
-6
6
As grandezas físicas são classificadas pelo critério do que é necessário para a sua total compreensão. As escalares exigem o módulo e a unidade de referência e as vetoriais exigem o módulo, a direção e o sentido. Neste sentido, classifique as grandezas em (E) escalar ou (V) vetorial.
( ) . Velocidade
( ) . Temperatura
( ) . Área
( ) . Torque
( ) . Força
É correta a sequência que corresponde a alternativa
V, V,V,E,V.
V, E,E,V,V.
V, E,V,E,V.
V, E,E,V,E.
E, E,E,V,V.
Os vetores podem ser representados, também, por meio dos versores 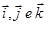 . Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja,
. Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja, 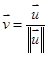 . Baseando-se nessas informações e considerando que
. Baseando-se nessas informações e considerando que pode-se concluir que o versor do vetor formado por
pode-se concluir que o versor do vetor formado por 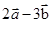 , está corretamente representado na alternativa
, está corretamente representado na alternativa
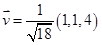
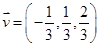
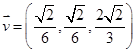

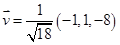
No plano cartesiano, considere os pontos A(-1, 2) e B(3, 4). Encontre a equação da reta r que passa por A e forma com o eixo das abscissas um ângulo de 45°, medido do eixo para a reta no sentido anti-horário.
y = x + 3
y = - x + 1
y = - x - 1
y = x - 1
y = x - 3
Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a

O produto escalar entre u e v considerando u=(3,3,3) e v=(-1,-5,4) está corretamente expresso na alternativa
2
-1
4
-6
6
As grandezas físicas são classificadas pelo critério do que é necessário para a sua total compreensão. As escalares exigem o módulo e a unidade de referência e as vetoriais exigem o módulo, a direção e o sentido. Neste sentido, classifique as grandezas em (E) escalar ou (V) vetorial.
( ) . Velocidade
( ) . Temperatura
( ) . Área
( ) . Torque
( ) . Força
É correta a sequência que corresponde a alternativa
V, V,V,E,V.
V, E,E,V,V.
V, E,V,E,V.
V, E,E,V,E.
E, E,E,V,V.
Os vetores podem ser representados, também, por meio dos versores 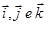 . Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja,
. Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja, 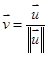 . Baseando-se nessas informações e considerando que
. Baseando-se nessas informações e considerando que pode-se concluir que o versor do vetor formado por
pode-se concluir que o versor do vetor formado por 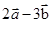 , está corretamente representado na alternativa
, está corretamente representado na alternativa
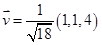
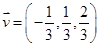
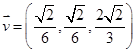

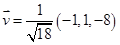
No plano cartesiano, considere os pontos A(-1, 2) e B(3, 4). Encontre a equação da reta r que passa por A e forma com o eixo das abscissas um ângulo de 45°, medido do eixo para a reta no sentido anti-horário.
y = x + 3
y = - x + 1
y = - x - 1
y = x - 1
y = x - 3
Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a

2
-1
4
-6
6
As grandezas físicas são classificadas pelo critério do que é necessário para a sua total compreensão. As escalares exigem o módulo e a unidade de referência e as vetoriais exigem o módulo, a direção e o sentido. Neste sentido, classifique as grandezas em (E) escalar ou (V) vetorial.
( ) . Velocidade
( ) . Temperatura
( ) . Área
( ) . Torque
( ) . Força
É correta a sequência que corresponde a alternativa
V, V,V,E,V.
V, E,E,V,V.
V, E,V,E,V.
V, E,E,V,E.
E, E,E,V,V.
Os vetores podem ser representados, também, por meio dos versores 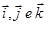 . Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja,
. Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja, 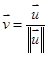 . Baseando-se nessas informações e considerando que
. Baseando-se nessas informações e considerando que pode-se concluir que o versor do vetor formado por
pode-se concluir que o versor do vetor formado por 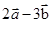 , está corretamente representado na alternativa
, está corretamente representado na alternativa
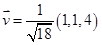
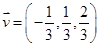
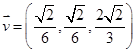

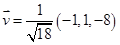
No plano cartesiano, considere os pontos A(-1, 2) e B(3, 4). Encontre a equação da reta r que passa por A e forma com o eixo das abscissas um ângulo de 45°, medido do eixo para a reta no sentido anti-horário.
y = x + 3
y = - x + 1
y = - x - 1
y = x - 1
y = x - 3
Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a

V, V,V,E,V.
V, E,E,V,V.
V, E,V,E,V.
V, E,E,V,E.
E, E,E,V,V.
Os vetores podem ser representados, também, por meio dos versores 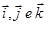 . Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja,
. Sabe-se que o versor de um vetor é a razão entre esse vetor e o seu módulo, ou seja, 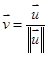 . Baseando-se nessas informações e considerando que
. Baseando-se nessas informações e considerando que pode-se concluir que o versor do vetor formado por
pode-se concluir que o versor do vetor formado por 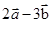 , está corretamente representado na alternativa
, está corretamente representado na alternativa
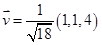
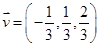
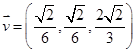

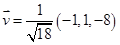
No plano cartesiano, considere os pontos A(-1, 2) e B(3, 4). Encontre a equação da reta r que passa por A e forma com o eixo das abscissas um ângulo de 45°, medido do eixo para a reta no sentido anti-horário.
y = x + 3
y = - x + 1
y = - x - 1
y = x - 1
y = x - 3
Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a

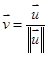 . Baseando-se nessas informações e considerando que
. Baseando-se nessas informações e considerando que![]()
![]()
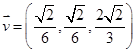

![]()
No plano cartesiano, considere os pontos A(-1, 2) e B(3, 4). Encontre a equação da reta r que passa por A e forma com o eixo das abscissas um ângulo de 45°, medido do eixo para a reta no sentido anti-horário.
y = x + 3
y = - x + 1
y = - x - 1
y = x - 1
y = x - 3
Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a

y = x + 3
y = - x + 1
y = - x - 1
y = x - 1
y = x - 3
Nos últimos anos, a televisão tem passado por uma verdadeira revolução, em termos de qualidade de imagem, som e interatividade com o telespectador. Essa transformação se deve à conversão do sinal analógico para o sinal digital. Entretanto, muitas cidades ainda não contam com essa nova tecnologia. Buscando levar esses benefícios a três cidades, uma emissora de televisão pretende construir uma nova torre de transmissão, que envie sinal às antenas A, B e C, já existentes nessas cidades. As localizações das antenas estão representadas no plano cartesiano:

A torre deve estar situada em um local equidistante das três antenas. O local adequado para a construção dessa torre corresponde ao ponto de coordenadas:
(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a


(50; 30)
(65; 35)
(45; 35)
(53; 20)
(60; 30)
Ao converter a equação polar %7D) em equação cartesiana, obtém-se:
em equação cartesiana, obtém-se:
x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a

x² + y² - 8(x+y)=0
x² + y² = 8(x-y)
x² - y² = 8(x+y)
x² + y² = x + y
x² - y² = 3(x+y)
Uma superfície esférica, de raio 13 cm, foi seccionada por um plano determinando uma circunferência, conforme ilustrado na figura. Neste caso, o raio dessa circunferência é igual a

