FUNDAMENTOS DE MATEMÁTICA ELEMENTAR

0,5.
-0,555.
-0,6428...
0,866...
0,707...
Um móvel parte da origem do arco na circunferência trigonométrica e percorre 97 845°. O número de voltas completas e o quadrante em que está a extremidade do arco pode ser indicado respectivamente em:
271 ; 4°
312 ; 3°
131 ; 4°
251 ; 2°
171 ; 2°
O gráfico a seguir, representa a função:
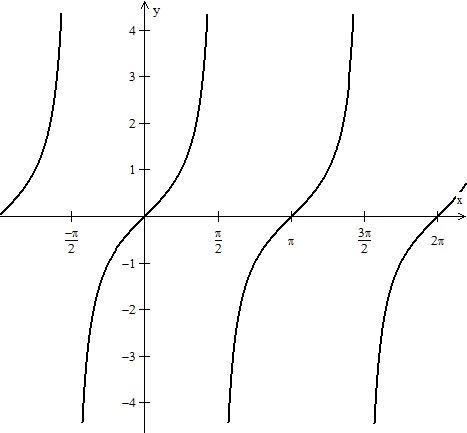
y = cos(x)
y = cotg(x)
y = tg(x)
y = - tg(x)
y = - cotg(x)

0,5.
-0,555.
-0,6428...
0,866...
0,707...
Um móvel parte da origem do arco na circunferência trigonométrica e percorre 97 845°. O número de voltas completas e o quadrante em que está a extremidade do arco pode ser indicado respectivamente em:
271 ; 4°
312 ; 3°
131 ; 4°
251 ; 2°
171 ; 2°
O gráfico a seguir, representa a função:

y = cos(x)
y = cotg(x)
y = tg(x)
y = - tg(x)
y = - cotg(x)

271 ; 4°
312 ; 3°
131 ; 4°
251 ; 2°
171 ; 2°
O gráfico a seguir, representa a função:

y = cos(x)
y = cotg(x)
y = tg(x)
y = - tg(x)
y = - cotg(x)


y = cos(x)
y = cotg(x)
y = tg(x)
y = - tg(x)
y = - cotg(x)