FUNDAMENTOS DE MATEMÁTICA ELEMENTAR
A parábola determinada pela função f: R -> R tal que f (x) = ax2 + bx + c, com a não nulo (diferente de 0), tem vértice de coordenadas (4, 2). Se o ponto de coordenadas (2, 0) pertence ao gráfico dessa função, então o produto a.b.c é igual a:
12
6
10
0,5
4
Uma empresa está realizando um balanço de vendas de um determinado produto e verifica que esse produto obtém lucro já na primeira semana de venda. O gráfico a seguir representa o lucro obtido desde o início do mês de junho até o dia 20.

O lucro (L) em função de t, obtido pela empresa pode ser representada algebricamente pela função:
f(t) = 20t - 4500
f(t) = 100t - 3000
f(t) = 150t + 4500
f(t) = 150t - 3000
f(t) = 150t + 3000

12000.
20000.
14000.
18000.
16000.

41/5
18/5
36/7
11/2
37/6
Sabendo que tg (x + y) = 33 e tg x = 3, considere a relação tg(x+y) = (tgx + tgy) / (1- tgx.tgy) e determine o valor de tg y. Esse valor é igual a:
0,3
0,4
0,5
0,1
0,2
Um caminhão custa hoje R$ 100000,00 e sofre uma desvalorização de 10% por ano de uso. Aproximadamente depois de quantos anos de uso o valor será igual a R$ 20 000,00?
Dados:
log 0,2 = - 0, 69897
log 0,9 = -0, 04576
30
20
15
19
17
Considere o ciclo a seguir,
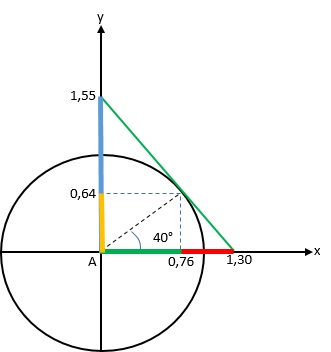
Podemos afirmar que:
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
1,3 corresponde a sen40° e 1,55 a cos40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,3 corresponde a cossec40° e 1,55 a sec40°.
Se x pertence ao 1º quadrante e cosx = 4/5 então podemos afirmar que os valores de senx, secx e cossecx são respectivamente:
12
6
10
0,5
4
Uma empresa está realizando um balanço de vendas de um determinado produto e verifica que esse produto obtém lucro já na primeira semana de venda. O gráfico a seguir representa o lucro obtido desde o início do mês de junho até o dia 20.

O lucro (L) em função de t, obtido pela empresa pode ser representada algebricamente pela função:
f(t) = 20t - 4500
f(t) = 100t - 3000
f(t) = 150t + 4500
f(t) = 150t - 3000
f(t) = 150t + 3000

12000.
20000.
14000.
18000.
16000.

41/5
18/5
36/7
11/2
37/6
Sabendo que tg (x + y) = 33 e tg x = 3, considere a relação tg(x+y) = (tgx + tgy) / (1- tgx.tgy) e determine o valor de tg y. Esse valor é igual a:
0,3
0,4
0,5
0,1
0,2
Um caminhão custa hoje R$ 100000,00 e sofre uma desvalorização de 10% por ano de uso. Aproximadamente depois de quantos anos de uso o valor será igual a R$ 20 000,00?
Dados:
log 0,2 = - 0, 69897
log 0,9 = -0, 04576
30
20
15
19
17
Considere o ciclo a seguir,

Podemos afirmar que:
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
1,3 corresponde a sen40° e 1,55 a cos40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,3 corresponde a cossec40° e 1,55 a sec40°.
Se x pertence ao 1º quadrante e cosx = 4/5 então podemos afirmar que os valores de senx, secx e cossecx são respectivamente:
f(t) = 20t - 4500
f(t) = 100t - 3000
f(t) = 150t + 4500
f(t) = 150t - 3000
f(t) = 150t + 3000

12000.
20000.
14000.
18000.
16000.

41/5
18/5
36/7
11/2
37/6
Sabendo que tg (x + y) = 33 e tg x = 3, considere a relação tg(x+y) = (tgx + tgy) / (1- tgx.tgy) e determine o valor de tg y. Esse valor é igual a:
0,3
0,4
0,5
0,1
0,2
Um caminhão custa hoje R$ 100000,00 e sofre uma desvalorização de 10% por ano de uso. Aproximadamente depois de quantos anos de uso o valor será igual a R$ 20 000,00?
Dados:
log 0,2 = - 0, 69897
log 0,9 = -0, 04576
30
20
15
19
17
Considere o ciclo a seguir,

Podemos afirmar que:
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
1,3 corresponde a sen40° e 1,55 a cos40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,3 corresponde a cossec40° e 1,55 a sec40°.
Se x pertence ao 1º quadrante e cosx = 4/5 então podemos afirmar que os valores de senx, secx e cossecx são respectivamente:
12000.
20000.
14000.
18000.
16000.

41/5
18/5
36/7
11/2
37/6
Sabendo que tg (x + y) = 33 e tg x = 3, considere a relação tg(x+y) = (tgx + tgy) / (1- tgx.tgy) e determine o valor de tg y. Esse valor é igual a:
0,3
0,4
0,5
0,1
0,2
Um caminhão custa hoje R$ 100000,00 e sofre uma desvalorização de 10% por ano de uso. Aproximadamente depois de quantos anos de uso o valor será igual a R$ 20 000,00?
Dados:
log 0,2 = - 0, 69897
log 0,9 = -0, 04576
30
20
15
19
17
Considere o ciclo a seguir,

Podemos afirmar que:
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
1,3 corresponde a sen40° e 1,55 a cos40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,3 corresponde a cossec40° e 1,55 a sec40°.
Se x pertence ao 1º quadrante e cosx = 4/5 então podemos afirmar que os valores de senx, secx e cossecx são respectivamente:

41/5
18/5
36/7
11/2
37/6
Sabendo que tg (x + y) = 33 e tg x = 3, considere a relação tg(x+y) = (tgx + tgy) / (1- tgx.tgy) e determine o valor de tg y. Esse valor é igual a:
0,3
0,4
0,5
0,1
0,2
Um caminhão custa hoje R$ 100000,00 e sofre uma desvalorização de 10% por ano de uso. Aproximadamente depois de quantos anos de uso o valor será igual a R$ 20 000,00?
Dados:
log 0,2 = - 0, 69897
log 0,9 = -0, 04576
30
20
15
19
17
Considere o ciclo a seguir,

Podemos afirmar que:
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
1,3 corresponde a sen40° e 1,55 a cos40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,3 corresponde a cossec40° e 1,55 a sec40°.
Se x pertence ao 1º quadrante e cosx = 4/5 então podemos afirmar que os valores de senx, secx e cossecx são respectivamente:
0,3
0,4
0,5
0,1
0,2
Um caminhão custa hoje R$ 100000,00 e sofre uma desvalorização de 10% por ano de uso. Aproximadamente depois de quantos anos de uso o valor será igual a R$ 20 000,00?
Dados:
log 0,2 = - 0, 69897
log 0,9 = -0, 04576
30
20
15
19
17
Considere o ciclo a seguir,

Podemos afirmar que:
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
1,3 corresponde a sen40° e 1,55 a cos40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,3 corresponde a cossec40° e 1,55 a sec40°.
Se x pertence ao 1º quadrante e cosx = 4/5 então podemos afirmar que os valores de senx, secx e cossecx são respectivamente:
30
20
15
19
17
Considere o ciclo a seguir,

Podemos afirmar que:
1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
1,3 corresponde a sen40° e 1,55 a cos40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,3 corresponde a cossec40° e 1,55 a sec40°.
Se x pertence ao 1º quadrante e cosx = 4/5 então podemos afirmar que os valores de senx, secx e cossecx são respectivamente:

1,55 corresponde a cossec40° e 1,3 a sec40°.
1,3 corresponde a sen40° e 0,76 a sec40°.
1,3 corresponde a sen40° e 1,55 a cos40°.
0,76 corresponde a sen40° e 0,64 a cos40°.
1,3 corresponde a cossec40° e 1,55 a sec40°.