FUNÇÕES COMPLEXAS
Obter a razão da PA, em que o 1º termo é -8 e o vigésimo termo é 30
2
-4
1
4
-2
Determine uma PA de quatro termos, sabendo que a soma dos dois primeiros é 29 e dos dois últimos é 89.
(7,22,36,51)
(3,28,43,46)
(9,20,35,54)
(8,21,36,51)
(7,22,37,52)
Os números complexos são escritos na sua forma algébrica da seguinte forma: a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo a = -4 + 3i , b = 5 - 6i e c = 4 - 3i , o valor de a.c + b será igual a:





Sabendo que Z é o resultado da operação, %7D-%7B%5Cleft(%7B2%7D-%7B3%7D%7Bi%7D%5Cright)%7D) , então o valor do conjugado de Z é igual a:
, então o valor do conjugado de Z é igual a:





Um terreno triangular, de esquina, tem 24 metros de frente para a rua A e 32 metros de frente para a rua B. Sabe-se que as ruas A e B formam um ângulo de 60º entre si. Com base nessas informações, determine a medida do terceiro lado do terreno. Em seguida, marque a alternativa que apresenta a resposta correta.





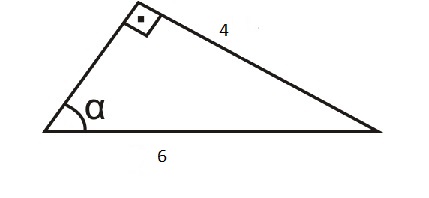
Observe o triângulo a seguir e encontre a tangente do ângulo  :
:
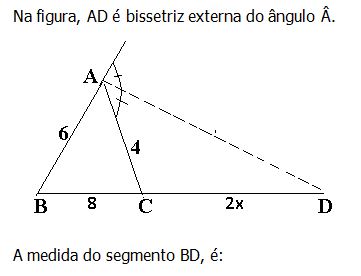
E correto que se afirma em:


`



2
-4
1
4
-2
Determine uma PA de quatro termos, sabendo que a soma dos dois primeiros é 29 e dos dois últimos é 89.
(7,22,36,51)
(3,28,43,46)
(9,20,35,54)
(8,21,36,51)
(7,22,37,52)
Os números complexos são escritos na sua forma algébrica da seguinte forma: a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo a = -4 + 3i , b = 5 - 6i e c = 4 - 3i , o valor de a.c + b será igual a:





Sabendo que Z é o resultado da operação, %7D-%7B%5Cleft(%7B2%7D-%7B3%7D%7Bi%7D%5Cright)%7D) , então o valor do conjugado de Z é igual a:
, então o valor do conjugado de Z é igual a:





Um terreno triangular, de esquina, tem 24 metros de frente para a rua A e 32 metros de frente para a rua B. Sabe-se que as ruas A e B formam um ângulo de 60º entre si. Com base nessas informações, determine a medida do terceiro lado do terreno. Em seguida, marque a alternativa que apresenta a resposta correta.





Observe o triângulo a seguir e encontre a tangente do ângulo  :
:

E correto que se afirma em:


`



(7,22,36,51)
(3,28,43,46)
(9,20,35,54)
(8,21,36,51)
(7,22,37,52)
Os números complexos são escritos na sua forma algébrica da seguinte forma: a + bi, sabemos que a e b são números reais e que o valor de a é a parte real do número complexo e que o valor de bi é a parte imaginária do número complexo. Sendo a = -4 + 3i , b = 5 - 6i e c = 4 - 3i , o valor de a.c + b será igual a:





Sabendo que Z é o resultado da operação, %7D-%7B%5Cleft(%7B2%7D-%7B3%7D%7Bi%7D%5Cright)%7D) , então o valor do conjugado de Z é igual a:
, então o valor do conjugado de Z é igual a:





Um terreno triangular, de esquina, tem 24 metros de frente para a rua A e 32 metros de frente para a rua B. Sabe-se que as ruas A e B formam um ângulo de 60º entre si. Com base nessas informações, determine a medida do terceiro lado do terreno. Em seguida, marque a alternativa que apresenta a resposta correta.





Observe o triângulo a seguir e encontre a tangente do ângulo  :
:

E correto que se afirma em:


`



Sabendo que Z é o resultado da operação, %7D-%7B%5Cleft(%7B2%7D-%7B3%7D%7Bi%7D%5Cright)%7D) , então o valor do conjugado de Z é igual a:
, então o valor do conjugado de Z é igual a:





Um terreno triangular, de esquina, tem 24 metros de frente para a rua A e 32 metros de frente para a rua B. Sabe-se que as ruas A e B formam um ângulo de 60º entre si. Com base nessas informações, determine a medida do terceiro lado do terreno. Em seguida, marque a alternativa que apresenta a resposta correta.





Observe o triângulo a seguir e encontre a tangente do ângulo  :
:

E correto que se afirma em:


`



Um terreno triangular, de esquina, tem 24 metros de frente para a rua A e 32 metros de frente para a rua B. Sabe-se que as ruas A e B formam um ângulo de 60º entre si. Com base nessas informações, determine a medida do terceiro lado do terreno. Em seguida, marque a alternativa que apresenta a resposta correta.





Observe o triângulo a seguir e encontre a tangente do ângulo  :
:

E correto que se afirma em:


`



Observe o triângulo a seguir e encontre a tangente do ângulo  :
:

E correto que se afirma em:


`




`