ESTRUTURA DE CONCRETO ARMADO II
Se em uma situação hipotética precisarmos de fazer um reforço estrutural em uma marquise, feita de uma laje em balanço, e para fazer este reforço precisarmos de fazer o escoramento, em que posição devemos colocar as escoras?
Nas laterais da marquise
no ponto central da marquise
Ao longo de toda a marquise
no final da marquise
Dimensionar a área de aço de uma escada residencial, de uma casa de alto padrão, que apresenta dois vãos paralelos e dois patamares. Os degraus tem uma altura de 16 cm e uma largura de 32 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 1,5 KN/m. Para fins de cálculo será considerado concreto C20 e aço CA-50, regularização de 1,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 12 cm; e o piso é de tábua corrida de imbuia, com espessura de 4 cm incluída a argamassa de assentamento, considere o d’ = 2,5 cm.
Obs: As medidas na planta baixa estão em metros. Utilize as mesmas para cálculo.

9,32 cm²/m
13,87 cm²/m
11,54 cm²/m
15,74 cm²/m
7,43 cm²/m
Qual é o valor do momento fletor máximo de calculo numa marquise, feita com laje em balanço com vão efetivo de 1,50 m
Dados: regularização feita de argamassa de cimento e areia com espessura de 2,5 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 4 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
Sabe-se ainda que as pessoas não têm acesso a esta marquise.
904,84 KN.cm/m
463,35 KN.cm/m
1125,30 KN.cm/m
785,63 KN.cm/m
727,30 KN.cm/m
Dimensione a área de aço de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 16 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 2 KN/m.Para fins de cálculo será considerado concreto C25 e aço CA-50, regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 12 cm; e o piso é de borracha com espessura de 5 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 2,5 cm.
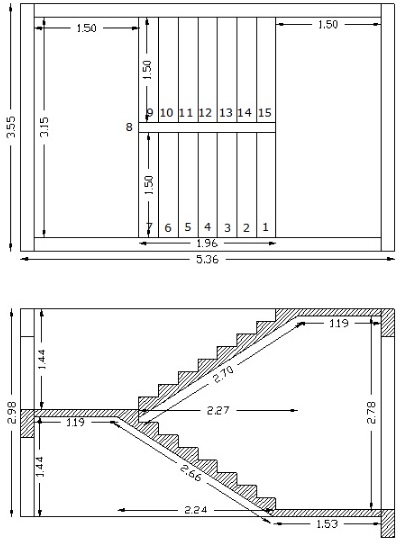
14,89 cm²
13,69 cm²
16,96 cm²
11,52 cm²
9,52 cm²
Calcule o momento fletor máximo (Mk) de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 18 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 3,2 kN/m. Regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 8 cm; e o piso é de arenito com espessura de 4 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2,5 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 3,0 cm.

32,69 KN.m/m
53,12 KN.m/m
25,76 KN.m/m
14,52 KN.m/m
45,76 KN.m/m
Qual é o valor da carga permanente de uma marquise, feita com laje em balanço.
Dados: regularização feita de argamassa de cimento e areia com espessura de 2 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 3 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
5 kN/m²
4,74 kN/m²
4,95 kN/m²
4,91 kN/m²
5,46 kN/m²
Para a viga de 25cmx60cm e Momento Fletor Característico Máximo de 415 kNm, executada com concreto Classe C30 e Aço CA-50, d'= 4cm, determine a Armadura tracionada que deverá existir para resistir ao esforço.
2,58 cm²
22,27 cm²
31,51 cm²
28,93 cm²
1,54 cm²
Considerando uma viga bi-apoiada de seção retangular com h = 40 cm, bw = 18 cm, e d’ = 3,0 cm, calcular a armadura tracionada, sabendo-se que a peça tem um vão teórico de 8 metros, carregamento total (já considerado o peso próprio) de 25 KN/m e são empregados concreto com fck = 25 MPa e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.
Nas laterais da marquise
no ponto central da marquise
Ao longo de toda a marquise
no final da marquise
Dimensionar a área de aço de uma escada residencial, de uma casa de alto padrão, que apresenta dois vãos paralelos e dois patamares. Os degraus tem uma altura de 16 cm e uma largura de 32 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 1,5 KN/m. Para fins de cálculo será considerado concreto C20 e aço CA-50, regularização de 1,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 12 cm; e o piso é de tábua corrida de imbuia, com espessura de 4 cm incluída a argamassa de assentamento, considere o d’ = 2,5 cm.
Obs: As medidas na planta baixa estão em metros. Utilize as mesmas para cálculo.

9,32 cm²/m
13,87 cm²/m
11,54 cm²/m
15,74 cm²/m
7,43 cm²/m
Qual é o valor do momento fletor máximo de calculo numa marquise, feita com laje em balanço com vão efetivo de 1,50 m
Dados: regularização feita de argamassa de cimento e areia com espessura de 2,5 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 4 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
Sabe-se ainda que as pessoas não têm acesso a esta marquise.
904,84 KN.cm/m
463,35 KN.cm/m
1125,30 KN.cm/m
785,63 KN.cm/m
727,30 KN.cm/m
Dimensione a área de aço de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 16 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 2 KN/m.Para fins de cálculo será considerado concreto C25 e aço CA-50, regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 12 cm; e o piso é de borracha com espessura de 5 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 2,5 cm.

14,89 cm²
13,69 cm²
16,96 cm²
11,52 cm²
9,52 cm²
Calcule o momento fletor máximo (Mk) de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 18 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 3,2 kN/m. Regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 8 cm; e o piso é de arenito com espessura de 4 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2,5 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 3,0 cm.

32,69 KN.m/m
53,12 KN.m/m
25,76 KN.m/m
14,52 KN.m/m
45,76 KN.m/m
Qual é o valor da carga permanente de uma marquise, feita com laje em balanço.
Dados: regularização feita de argamassa de cimento e areia com espessura de 2 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 3 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
5 kN/m²
4,74 kN/m²
4,95 kN/m²
4,91 kN/m²
5,46 kN/m²
Para a viga de 25cmx60cm e Momento Fletor Característico Máximo de 415 kNm, executada com concreto Classe C30 e Aço CA-50, d'= 4cm, determine a Armadura tracionada que deverá existir para resistir ao esforço.
2,58 cm²
22,27 cm²
31,51 cm²
28,93 cm²
1,54 cm²
Considerando uma viga bi-apoiada de seção retangular com h = 40 cm, bw = 18 cm, e d’ = 3,0 cm, calcular a armadura tracionada, sabendo-se que a peça tem um vão teórico de 8 metros, carregamento total (já considerado o peso próprio) de 25 KN/m e são empregados concreto com fck = 25 MPa e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.
9,32 cm²/m
13,87 cm²/m
11,54 cm²/m
15,74 cm²/m
7,43 cm²/m
Qual é o valor do momento fletor máximo de calculo numa marquise, feita com laje em balanço com vão efetivo de 1,50 m
Dados: regularização feita de argamassa de cimento e areia com espessura de 2,5 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 4 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
Sabe-se ainda que as pessoas não têm acesso a esta marquise.
904,84 KN.cm/m
463,35 KN.cm/m
1125,30 KN.cm/m
785,63 KN.cm/m
727,30 KN.cm/m
Dimensione a área de aço de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 16 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 2 KN/m.Para fins de cálculo será considerado concreto C25 e aço CA-50, regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 12 cm; e o piso é de borracha com espessura de 5 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 2,5 cm.

14,89 cm²
13,69 cm²
16,96 cm²
11,52 cm²
9,52 cm²
Calcule o momento fletor máximo (Mk) de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 18 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 3,2 kN/m. Regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 8 cm; e o piso é de arenito com espessura de 4 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2,5 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 3,0 cm.

32,69 KN.m/m
53,12 KN.m/m
25,76 KN.m/m
14,52 KN.m/m
45,76 KN.m/m
Qual é o valor da carga permanente de uma marquise, feita com laje em balanço.
Dados: regularização feita de argamassa de cimento e areia com espessura de 2 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 3 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
5 kN/m²
4,74 kN/m²
4,95 kN/m²
4,91 kN/m²
5,46 kN/m²
Para a viga de 25cmx60cm e Momento Fletor Característico Máximo de 415 kNm, executada com concreto Classe C30 e Aço CA-50, d'= 4cm, determine a Armadura tracionada que deverá existir para resistir ao esforço.
2,58 cm²
22,27 cm²
31,51 cm²
28,93 cm²
1,54 cm²
Considerando uma viga bi-apoiada de seção retangular com h = 40 cm, bw = 18 cm, e d’ = 3,0 cm, calcular a armadura tracionada, sabendo-se que a peça tem um vão teórico de 8 metros, carregamento total (já considerado o peso próprio) de 25 KN/m e são empregados concreto com fck = 25 MPa e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.
904,84 KN.cm/m
463,35 KN.cm/m
1125,30 KN.cm/m
785,63 KN.cm/m
727,30 KN.cm/m
Dimensione a área de aço de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 16 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 2 KN/m.Para fins de cálculo será considerado concreto C25 e aço CA-50, regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 12 cm; e o piso é de borracha com espessura de 5 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 2,5 cm.

14,89 cm²
13,69 cm²
16,96 cm²
11,52 cm²
9,52 cm²
Calcule o momento fletor máximo (Mk) de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 18 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 3,2 kN/m. Regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 8 cm; e o piso é de arenito com espessura de 4 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2,5 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 3,0 cm.

32,69 KN.m/m
53,12 KN.m/m
25,76 KN.m/m
14,52 KN.m/m
45,76 KN.m/m
Qual é o valor da carga permanente de uma marquise, feita com laje em balanço.
Dados: regularização feita de argamassa de cimento e areia com espessura de 2 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 3 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
5 kN/m²
4,74 kN/m²
4,95 kN/m²
4,91 kN/m²
5,46 kN/m²
Para a viga de 25cmx60cm e Momento Fletor Característico Máximo de 415 kNm, executada com concreto Classe C30 e Aço CA-50, d'= 4cm, determine a Armadura tracionada que deverá existir para resistir ao esforço.
2,58 cm²
22,27 cm²
31,51 cm²
28,93 cm²
1,54 cm²
Considerando uma viga bi-apoiada de seção retangular com h = 40 cm, bw = 18 cm, e d’ = 3,0 cm, calcular a armadura tracionada, sabendo-se que a peça tem um vão teórico de 8 metros, carregamento total (já considerado o peso próprio) de 25 KN/m e são empregados concreto com fck = 25 MPa e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.

14,89 cm²
13,69 cm²
16,96 cm²
11,52 cm²
9,52 cm²
Calcule o momento fletor máximo (Mk) de uma escada de um prédio residencial com 18 andares, que apresenta dois vãos paralelos, conforme figura abaixo. Os degraus tem uma altura de 18 cm e uma largura de 28 cm. No lado interno dos degraus existe um peitoril com carga correspondente a 3,2 kN/m. Regularização de 2,5 cm feita com argamassa de cimento e areia; a laje das escadas tem espessura de 8 cm; e o piso é de arenito com espessura de 4 cm incluida a argamassa de assentamento; foi rebocada na parte de baixo com gesso com espessura de 2,5 cm. Obs: Para fins de cálculo considere que o carregamento dos degraus e dos patamares esteja projetado em planta, ou seja dimensões retiradas da planta baixa e não do corte, para o calculo da laje considere o vão de eixo a eixo, considerando as lajes separadas no meio, calcule o carregamento do patamar separado do carregamento dos degraus, para o calculo da altura média do degrau considere a altura da laje somada a metade da altura do degrau, para o calculo do peso próprio do degrau multiplique a altura média pelo comprimento dos degraus em projeção, considere o d’ = 3,0 cm.

32,69 KN.m/m
53,12 KN.m/m
25,76 KN.m/m
14,52 KN.m/m
45,76 KN.m/m
Qual é o valor da carga permanente de uma marquise, feita com laje em balanço.
Dados: regularização feita de argamassa de cimento e areia com espessura de 2 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 3 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
5 kN/m²
4,74 kN/m²
4,95 kN/m²
4,91 kN/m²
5,46 kN/m²
Para a viga de 25cmx60cm e Momento Fletor Característico Máximo de 415 kNm, executada com concreto Classe C30 e Aço CA-50, d'= 4cm, determine a Armadura tracionada que deverá existir para resistir ao esforço.
2,58 cm²
22,27 cm²
31,51 cm²
28,93 cm²
1,54 cm²
Considerando uma viga bi-apoiada de seção retangular com h = 40 cm, bw = 18 cm, e d’ = 3,0 cm, calcular a armadura tracionada, sabendo-se que a peça tem um vão teórico de 8 metros, carregamento total (já considerado o peso próprio) de 25 KN/m e são empregados concreto com fck = 25 MPa e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.

32,69 KN.m/m
53,12 KN.m/m
25,76 KN.m/m
14,52 KN.m/m
45,76 KN.m/m
Qual é o valor da carga permanente de uma marquise, feita com laje em balanço.
Dados: regularização feita de argamassa de cimento e areia com espessura de 2 cm;
laje de concreto armado com 15 cm de espessura;
Reboco feito com argamassa de cal, cimento e areia com espessura de 3 cm;
impermeabilização, cujo peso específico é o mesmo do plástico em folhas, com espessura de 1 cm
5 kN/m²
4,74 kN/m²
4,95 kN/m²
4,91 kN/m²
5,46 kN/m²
Para a viga de 25cmx60cm e Momento Fletor Característico Máximo de 415 kNm, executada com concreto Classe C30 e Aço CA-50, d'= 4cm, determine a Armadura tracionada que deverá existir para resistir ao esforço.
2,58 cm²
22,27 cm²
31,51 cm²
28,93 cm²
1,54 cm²
Considerando uma viga bi-apoiada de seção retangular com h = 40 cm, bw = 18 cm, e d’ = 3,0 cm, calcular a armadura tracionada, sabendo-se que a peça tem um vão teórico de 8 metros, carregamento total (já considerado o peso próprio) de 25 KN/m e são empregados concreto com fck = 25 MPa e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.
5 kN/m²
4,74 kN/m²
4,95 kN/m²
4,91 kN/m²
5,46 kN/m²
Para a viga de 25cmx60cm e Momento Fletor Característico Máximo de 415 kNm, executada com concreto Classe C30 e Aço CA-50, d'= 4cm, determine a Armadura tracionada que deverá existir para resistir ao esforço.
2,58 cm²
22,27 cm²
31,51 cm²
28,93 cm²
1,54 cm²
Considerando uma viga bi-apoiada de seção retangular com h = 40 cm, bw = 18 cm, e d’ = 3,0 cm, calcular a armadura tracionada, sabendo-se que a peça tem um vão teórico de 8 metros, carregamento total (já considerado o peso próprio) de 25 KN/m e são empregados concreto com fck = 25 MPa e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.
2,58 cm²
22,27 cm²
31,51 cm²
28,93 cm²
1,54 cm²
Considerando uma viga bi-apoiada de seção retangular com h = 40 cm, bw = 18 cm, e d’ = 3,0 cm, calcular a armadura tracionada, sabendo-se que a peça tem um vão teórico de 8 metros, carregamento total (já considerado o peso próprio) de 25 KN/m e são empregados concreto com fck = 25 MPa e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.
9,68 cm²
24,85 cm²
11,47 cm²
21,15 cm²
31,25 cm²
Com os dados do pilar da figura abaixo, considere como sendo um pilar de extremidade. Determinar o momento fletor de cálculo de 2ª ordem pelo método do pilar-padrão com curvatura aproximada.
Concreto C25, Aço CA-50, d’ = 3cm, Nk = 450 kN, Seção 14 x 35, lex = ley = 320 cm

2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm
Calcular a altura útil (mínima) que a viga de base 14 cm terá que atingir para que não necessite de armadura de compressão. Considere a profundidade de LN de acordo com as condições de Dutilidade apresentada na NBR 6118/2014.
Dados: concreto C-20, momento característico (Mk)= 285 KN.m e aço CA-50.
2057,14 KN.cm
2540,85 KN.cm
3024,52 KN.cm
1845,67 KN.cm
3250,50 KN.cm