ESTATÍSTICA INFERENCIAL
Em uma equação de regressão envolvendo 30 observações, foi obtida a seguinte equação de regressão estimada:
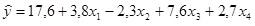
Qual o valor estimado de y quando x1 = 10, x2 = 5, x3 = 1 e x4 = 2? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
80,20.
102,30.
57,10.
48,90.
32,40.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 306.).
Os dados de perfil de audiência coletados no web site da ESPN Sportszone mostraram que 26% dos usuários eram mulheres (USA Today, 20 de janeiro de 1998). Considere que essa porcentagem foi baseada numa amostra de 400 usuários. Com uma confiança de 95%, qual a margem de erro associada com a proporção estimada de usuários que são mulheres? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 1,56%.
± 4,30%.
± 2,86%.
± 3,56%.
± 5,68%.
Na equação de regressão múltipla y = β0 + β1x1 + β2x2 + β3x3 + ε, como você testaria a hipótese conjunta β1 = β2 = β3?
Verificando o valor do coeficiente de determinação múltipla: rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse menor que 1.
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β1: se t teste for maior que t crítico, não rejeitaria a hipótese de que β1 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
Verificando o valor do coeficiente de determinação múltipla: não rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse maior que 1.
Comparando o valor da estatística F teste com o valor da estatística F crítico: se F teste for maior que F crítico, rejeitaria a hipótese β1 = β2 = β3 .
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β2: se t teste for maior que t crítico, não rejeitaria a hipótese de que β2 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 344.)
No último ano o número de almoços servidos na cantina de uma escola de ensino fundamental foi distribuído normalmente com uma média de 300 almoços por dia. No início do corrente ano, o preço de um almoço foi aumentado em 25 centavos. Uma amostra de seis dias duramente os meses de setembro, outubro e novembro forneceu o número de crianças que efetivamente almoçaram: 290, 275, 310, 260, 270 e 275. Estes dados indicam que o número médio de almoços por dia tenha caído desde o último ano? Assinale a alternativa que indica as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se o número médio de almoços caiu desde o último ano.
Ho: µ < 300 e Ha: µ ≥ 300
Ho: µ ≤ 300 e Ha: µ > 300
Ho: µ ≥ 300 e Ha: µ < 300
Ho: µ ≠ 300 e Ha: µ = 300
Ho: µ = 300 e Ha: µ ≠ 300
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
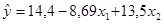, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
98,57 pontos.
28,49 pontos.
25,60 pontos.
58,46 pontos.
67,39 pontos
A equação de regressão estimada para um modelo envolvendo duas variáveis independentes e 10 observações é apresentada a seguir:
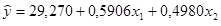
Qual o valor estimado de y quando x1 = 180 e x2 = 310? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
209,96.
119,96.
289,96.
239,96.
219,96.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
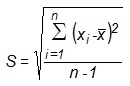
1,24 pontos.
1,19 pontos.
1,22 pontos.
1,14 pontos.
1,16 pontos.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
A empresa Instituto de Verificação de Opinião Pública entrevistou 2500 eleitores de um total de 100.000 eleitores de certo município. Do total de entrevistados, 750 afirmaram que votarão no candidato X para prefeito. A respeito dos procedimentos realizados pela empresa, julgue as seguintes afirmações:
I. A população de eleitores é igual a 100.000.
II. O tamanho da amostra é de 2.500 eleitores.
III. A proporção amostral dos eleitores que declararam votar no candidato X é de 40%.
IV. A estimativa pontual dos eleitores da população que votarão no candidato X é de 30%.
Estão corretas as afirmações:
80,20.
102,30.
57,10.
48,90.
32,40.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 306.).
Os dados de perfil de audiência coletados no web site da ESPN Sportszone mostraram que 26% dos usuários eram mulheres (USA Today, 20 de janeiro de 1998). Considere que essa porcentagem foi baseada numa amostra de 400 usuários. Com uma confiança de 95%, qual a margem de erro associada com a proporção estimada de usuários que são mulheres? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 1,56%.
± 4,30%.
± 2,86%.
± 3,56%.
± 5,68%.
Na equação de regressão múltipla y = β0 + β1x1 + β2x2 + β3x3 + ε, como você testaria a hipótese conjunta β1 = β2 = β3?
Verificando o valor do coeficiente de determinação múltipla: rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse menor que 1.
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β1: se t teste for maior que t crítico, não rejeitaria a hipótese de que β1 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
Verificando o valor do coeficiente de determinação múltipla: não rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse maior que 1.
Comparando o valor da estatística F teste com o valor da estatística F crítico: se F teste for maior que F crítico, rejeitaria a hipótese β1 = β2 = β3 .
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β2: se t teste for maior que t crítico, não rejeitaria a hipótese de que β2 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 344.)
No último ano o número de almoços servidos na cantina de uma escola de ensino fundamental foi distribuído normalmente com uma média de 300 almoços por dia. No início do corrente ano, o preço de um almoço foi aumentado em 25 centavos. Uma amostra de seis dias duramente os meses de setembro, outubro e novembro forneceu o número de crianças que efetivamente almoçaram: 290, 275, 310, 260, 270 e 275. Estes dados indicam que o número médio de almoços por dia tenha caído desde o último ano? Assinale a alternativa que indica as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se o número médio de almoços caiu desde o último ano.
Ho: µ < 300 e Ha: µ ≥ 300
Ho: µ ≤ 300 e Ha: µ > 300
Ho: µ ≥ 300 e Ha: µ < 300
Ho: µ ≠ 300 e Ha: µ = 300
Ho: µ = 300 e Ha: µ ≠ 300
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
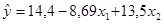, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
98,57 pontos.
28,49 pontos.
25,60 pontos.
58,46 pontos.
67,39 pontos
A equação de regressão estimada para um modelo envolvendo duas variáveis independentes e 10 observações é apresentada a seguir:
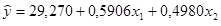
Qual o valor estimado de y quando x1 = 180 e x2 = 310? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
209,96.
119,96.
289,96.
239,96.
219,96.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
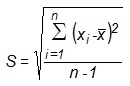
1,24 pontos.
1,19 pontos.
1,22 pontos.
1,14 pontos.
1,16 pontos.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
A empresa Instituto de Verificação de Opinião Pública entrevistou 2500 eleitores de um total de 100.000 eleitores de certo município. Do total de entrevistados, 750 afirmaram que votarão no candidato X para prefeito. A respeito dos procedimentos realizados pela empresa, julgue as seguintes afirmações:
I. A população de eleitores é igual a 100.000.
II. O tamanho da amostra é de 2.500 eleitores.
III. A proporção amostral dos eleitores que declararam votar no candidato X é de 40%.
IV. A estimativa pontual dos eleitores da população que votarão no candidato X é de 30%.
Estão corretas as afirmações:
± 1,56%.
± 4,30%.
± 2,86%.
± 3,56%.
± 5,68%.
Na equação de regressão múltipla y = β0 + β1x1 + β2x2 + β3x3 + ε, como você testaria a hipótese conjunta β1 = β2 = β3?
Verificando o valor do coeficiente de determinação múltipla: rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse menor que 1.
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β1: se t teste for maior que t crítico, não rejeitaria a hipótese de que β1 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
Verificando o valor do coeficiente de determinação múltipla: não rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse maior que 1.
Comparando o valor da estatística F teste com o valor da estatística F crítico: se F teste for maior que F crítico, rejeitaria a hipótese β1 = β2 = β3 .
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β2: se t teste for maior que t crítico, não rejeitaria a hipótese de que β2 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 344.)
No último ano o número de almoços servidos na cantina de uma escola de ensino fundamental foi distribuído normalmente com uma média de 300 almoços por dia. No início do corrente ano, o preço de um almoço foi aumentado em 25 centavos. Uma amostra de seis dias duramente os meses de setembro, outubro e novembro forneceu o número de crianças que efetivamente almoçaram: 290, 275, 310, 260, 270 e 275. Estes dados indicam que o número médio de almoços por dia tenha caído desde o último ano? Assinale a alternativa que indica as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se o número médio de almoços caiu desde o último ano.
Ho: µ < 300 e Ha: µ ≥ 300
Ho: µ ≤ 300 e Ha: µ > 300
Ho: µ ≥ 300 e Ha: µ < 300
Ho: µ ≠ 300 e Ha: µ = 300
Ho: µ = 300 e Ha: µ ≠ 300
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
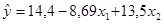, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
98,57 pontos.
28,49 pontos.
25,60 pontos.
58,46 pontos.
67,39 pontos
A equação de regressão estimada para um modelo envolvendo duas variáveis independentes e 10 observações é apresentada a seguir:
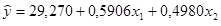
Qual o valor estimado de y quando x1 = 180 e x2 = 310? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
209,96.
119,96.
289,96.
239,96.
219,96.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
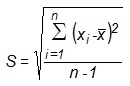
1,24 pontos.
1,19 pontos.
1,22 pontos.
1,14 pontos.
1,16 pontos.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
A empresa Instituto de Verificação de Opinião Pública entrevistou 2500 eleitores de um total de 100.000 eleitores de certo município. Do total de entrevistados, 750 afirmaram que votarão no candidato X para prefeito. A respeito dos procedimentos realizados pela empresa, julgue as seguintes afirmações:
I. A população de eleitores é igual a 100.000.
II. O tamanho da amostra é de 2.500 eleitores.
III. A proporção amostral dos eleitores que declararam votar no candidato X é de 40%.
IV. A estimativa pontual dos eleitores da população que votarão no candidato X é de 30%.
Estão corretas as afirmações:
Verificando o valor do coeficiente de determinação múltipla: rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse menor que 1.
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β1: se t teste for maior que t crítico, não rejeitaria a hipótese de que β1 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
Verificando o valor do coeficiente de determinação múltipla: não rejeitaria a hipótese β1 = β2 = β3 se o coeficiente de determinação múltipla fosse maior que 1.
Comparando o valor da estatística F teste com o valor da estatística F crítico: se F teste for maior que F crítico, rejeitaria a hipótese β1 = β2 = β3 .
Comparando o valor da estatística t de teste com o valor da estatística t crítico do coeficiente β2: se t teste for maior que t crítico, não rejeitaria a hipótese de que β2 é igual a zero e concluiria que a igualdade β1 = β2 = β3 é válida.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 344.)
No último ano o número de almoços servidos na cantina de uma escola de ensino fundamental foi distribuído normalmente com uma média de 300 almoços por dia. No início do corrente ano, o preço de um almoço foi aumentado em 25 centavos. Uma amostra de seis dias duramente os meses de setembro, outubro e novembro forneceu o número de crianças que efetivamente almoçaram: 290, 275, 310, 260, 270 e 275. Estes dados indicam que o número médio de almoços por dia tenha caído desde o último ano? Assinale a alternativa que indica as hipóteses nula (Ho) e alternativa (Ha) adequadas para testar se o número médio de almoços caiu desde o último ano.
Ho: µ < 300 e Ha: µ ≥ 300
Ho: µ ≤ 300 e Ha: µ > 300
Ho: µ ≥ 300 e Ha: µ < 300
Ho: µ ≠ 300 e Ha: µ = 300
Ho: µ = 300 e Ha: µ ≠ 300
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
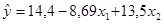, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
98,57 pontos.
28,49 pontos.
25,60 pontos.
58,46 pontos.
67,39 pontos
A equação de regressão estimada para um modelo envolvendo duas variáveis independentes e 10 observações é apresentada a seguir:
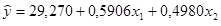
Qual o valor estimado de y quando x1 = 180 e x2 = 310? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
209,96.
119,96.
289,96.
239,96.
219,96.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
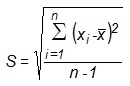
1,24 pontos.
1,19 pontos.
1,22 pontos.
1,14 pontos.
1,16 pontos.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
A empresa Instituto de Verificação de Opinião Pública entrevistou 2500 eleitores de um total de 100.000 eleitores de certo município. Do total de entrevistados, 750 afirmaram que votarão no candidato X para prefeito. A respeito dos procedimentos realizados pela empresa, julgue as seguintes afirmações:
I. A população de eleitores é igual a 100.000.
II. O tamanho da amostra é de 2.500 eleitores.
III. A proporção amostral dos eleitores que declararam votar no candidato X é de 40%.
IV. A estimativa pontual dos eleitores da população que votarão no candidato X é de 30%.
Estão corretas as afirmações:
Ho: µ < 300 e Ha: µ ≥ 300
Ho: µ ≤ 300 e Ha: µ > 300
Ho: µ ≥ 300 e Ha: µ < 300
Ho: µ ≠ 300 e Ha: µ = 300
Ho: µ = 300 e Ha: µ ≠ 300
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 501.)
O diretor de recursos humanos da Electronics Associates desenvolveu a seguinte equação de regressão estimada, relacionando a pontuação de um funcionário em um teste de satisfação no trabalho com seu tempo de serviço e seu salário.
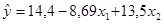, em que:
x1 = tempo de serviço (anos);
x2 = salário (dólares);
y = pontuação no teste de satisfação no trabalho (maiores valores indicam mais satisfação).
É correto afirmar que a pontuação estimada do teste de satisfação no trabalho para um funcionário que teve quatro anos de serviço e ganha US$ 6,50 por hora é igual a:
98,57 pontos.
28,49 pontos.
25,60 pontos.
58,46 pontos.
67,39 pontos
A equação de regressão estimada para um modelo envolvendo duas variáveis independentes e 10 observações é apresentada a seguir:
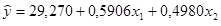
Qual o valor estimado de y quando x1 = 180 e x2 = 310? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
209,96.
119,96.
289,96.
239,96.
219,96.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
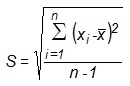
1,24 pontos.
1,19 pontos.
1,22 pontos.
1,14 pontos.
1,16 pontos.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
A empresa Instituto de Verificação de Opinião Pública entrevistou 2500 eleitores de um total de 100.000 eleitores de certo município. Do total de entrevistados, 750 afirmaram que votarão no candidato X para prefeito. A respeito dos procedimentos realizados pela empresa, julgue as seguintes afirmações:
I. A população de eleitores é igual a 100.000.
II. O tamanho da amostra é de 2.500 eleitores.
III. A proporção amostral dos eleitores que declararam votar no candidato X é de 40%.
IV. A estimativa pontual dos eleitores da população que votarão no candidato X é de 30%.
Estão corretas as afirmações:
, em que:98,57 pontos.
28,49 pontos.
25,60 pontos.
58,46 pontos.
67,39 pontos
A equação de regressão estimada para um modelo envolvendo duas variáveis independentes e 10 observações é apresentada a seguir:
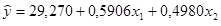
Qual o valor estimado de y quando x1 = 180 e x2 = 310? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
209,96.
119,96.
289,96.
239,96.
219,96.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
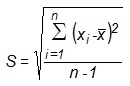
1,24 pontos.
1,19 pontos.
1,22 pontos.
1,14 pontos.
1,16 pontos.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
A empresa Instituto de Verificação de Opinião Pública entrevistou 2500 eleitores de um total de 100.000 eleitores de certo município. Do total de entrevistados, 750 afirmaram que votarão no candidato X para prefeito. A respeito dos procedimentos realizados pela empresa, julgue as seguintes afirmações:
I. A população de eleitores é igual a 100.000.
II. O tamanho da amostra é de 2.500 eleitores.
III. A proporção amostral dos eleitores que declararam votar no candidato X é de 40%.
IV. A estimativa pontual dos eleitores da população que votarão no candidato X é de 30%.
Estão corretas as afirmações:
209,96.
119,96.
289,96.
239,96.
219,96.
As notas finais da disciplina Matemática Básica para uma amostra de 20 alunos dos cursos de graduação de certa faculdade são apresentadas a seguir:
6,2 6,3 5,8
7,5 5,3 6,3
7,4 4,7 8,4
7,1 6,5 6,6
6,8 7,5 8,2
7,0 8,6 8,8
5,0 7,4
Qual a estimativa pontual do desvio padrão das notas da disciplina Matemática Básica? Faça os cálculos com quatro casas decimais e arredonde o resultado final para duas casas decimais.
Dado adicional:
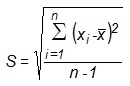
1,24 pontos.
1,19 pontos.
1,22 pontos.
1,14 pontos.
1,16 pontos.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
A empresa Instituto de Verificação de Opinião Pública entrevistou 2500 eleitores de um total de 100.000 eleitores de certo município. Do total de entrevistados, 750 afirmaram que votarão no candidato X para prefeito. A respeito dos procedimentos realizados pela empresa, julgue as seguintes afirmações:
I. A população de eleitores é igual a 100.000.
II. O tamanho da amostra é de 2.500 eleitores.
III. A proporção amostral dos eleitores que declararam votar no candidato X é de 40%.
IV. A estimativa pontual dos eleitores da população que votarão no candidato X é de 30%.
Estão corretas as afirmações:
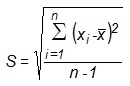
1,24 pontos.
1,19 pontos.
1,22 pontos.
1,14 pontos.
1,16 pontos.
O jornal O Correio, de Salvador, divulgou, em 08 de junho de 2016, a seguinte notícia: “Uma pesquisa de intenções de voto da Confederação Nacional de Transportes (CNT)/MDA aponta o ex-presidente Luiz Inácio Lula da Silva como o principal candidato à presidência da República em 2018. O presidente em exercício, Michel Temer, e o deputado Jair Bolsonaro (PP-RJ) ficaram empatados em quinto lugar no questionário espontâneo. Os números foram divulgados nesta quarta-feira (8).
Na intenção de voto espontânea, Lula aparece com 8,6%, seguido pelo senador Aécio Neves (5,7%), pela presidente da Rede, Marina Silva (3,8%) e pela presidente afastada, Dilma Rousseff (2,3%). Temer e Bolsonaro estão com 2,1% e Ciro Gomes, pré-candidato do PDT, aparece com 1,2%. Esta é a primeira pesquisa divulgada por um grande instituto desde o início do governo interino de Temer.
Ao todo, foram entrevistadas 2.002 pessoas, em 137 municípios de 25 estados brasileiros, entre os dias 2 e 5 de junho, com 95% de nível de confiança. ” (Disponível em http://www.correio24horas.com.br/detalhe/brasil/noticia/lula-e-favorito-dos-brasileiros-para-eleicoes-presidenciais-de-2018-diz-pesquisa. Acesso: 14/07/2016.)
Qual a margem de erro associada com a porcentagem estimada de eleitores que declararam votar no candidato Lula ao responderem o questionário espontâneo? Faça os cálculos com seis casas decimais e arredonde o resultado final para duas casas decimais.
Dados adicionais:
Z=1,96
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
A empresa Instituto de Verificação de Opinião Pública entrevistou 2500 eleitores de um total de 100.000 eleitores de certo município. Do total de entrevistados, 750 afirmaram que votarão no candidato X para prefeito. A respeito dos procedimentos realizados pela empresa, julgue as seguintes afirmações:
I. A população de eleitores é igual a 100.000.
II. O tamanho da amostra é de 2.500 eleitores.
III. A proporção amostral dos eleitores que declararam votar no candidato X é de 40%.
IV. A estimativa pontual dos eleitores da população que votarão no candidato X é de 30%.
Estão corretas as afirmações:
± 4,23%
± 5,23%
± 3,23%
± 2,23%
± 1,23%
, em que: