ELETROMAGNETISMO
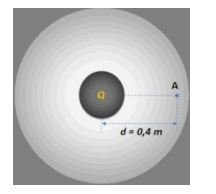
Na figura abaixo, determine aproximadamente a intensidade do potencial elétrico situado em um ponto A, sabendo que a carga elétrica do corpo vale de 6.10-9 C,
considere a constante eletrostática igual a 9.109 N.m2/C2
100 V
135 V
400 V
190 V
300 V
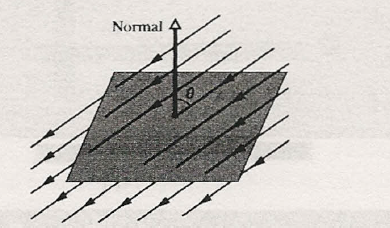
A figura abaixo mostra a superfície quadrada que tem 3,2 mm de lado e está imersa em um campo elétrico uniforme de módulo E = 1800 N/C e
com linhas de campo fazendo um ângulo de 35° com a normal, como mostra a figura.
Tome esta normal como apontando "para fora", como se a superfície fosse a tampa de uma caixa. Determine aproximadamente o fluxo elétrico em N.m2/C
através da superfície e considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
-3,256
-8,36
-0,015
-0,789
-2,56
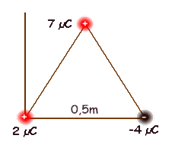
Três esferas com cargas de 2.10-6C, 7.10-6C e -4.10-6C são colocadas nos vértices de um triângulo equilátero, de 0,5 m de lado. Determinar aproximadamente a intensidade da força resultante sobre a esfera de 7.10-6C. Considere a constante eletrostática igual a 9.109 N.m²/c².
2,56 N
6,35 N
0,872 N
8,99 N
10 N
Em certa situação, temos uma placa não-condutora infinita que possui uma densidade superficial de cargas igual a +5,80 . 10-12C/m2.
Qual é aproximadamente o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga q = +1,6. 10-19C é deslocada
da superfície da placa para um ponto P situado a uma distância d = 3,56. 10-2m da superfície da placa?
considere a constante eletrostática igual a 8,99 × 109 N.m2/C2.
6.10-19 J
8.10-19 J
1,87.10-21 J
1,6.10-19 J
6.10-20 J
Determine o campo magnético em um ponto situado nas proximidades do centro de um solenóide longo de comprimento 15 cm e raio 2.50 cm e que possui 600 espiras enroladas de modo compacto. Sabendo que a corrente que passa nas espiras e igual a 8 A. Considere a permeabilidade igual a 4`pi.10-7`
0,0402 T
3 T
2 T
1,5 T
1,2 T
Determine aproximadamente intensidade de uma carga elétrica, sabendo que o campo elétrico a 50 cm de distância tem intensidade de 2N/C, considere a constante eletrostatica igual a 8, 99 · 109 Nm2/C2, sendo 1 pC = 10-12 C.
12 pC
56 pC
30 pC
40 pC
25 pC
Considere uma esfera condutora com 10 cm de raio. Sabendo que o campo elétrico a 15 cm do centro da esfera tem um módulo de 3 × 10 3 N/C e aponta para o centro da esfera, Determine aproximadamente a carga desta esfera. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
7,5 · 10-10 C
7,5 · 10-9 C
7,5 · 10-11 C
7,5 · 10-12 C
7,5 · 10-13 C
Calcule a força elétrica resultante na carga Q1= 6μC, localizada em P1(1, 2, –3), que sofre influência de Q2 = 13μC na posição P2(2 , – 4, 1) e Q3= -7μC na posição P3(3, –2,–2). Considere εr= 1,8.
Note que:


100 V
135 V
400 V
190 V
300 V
A figura abaixo mostra a superfície quadrada que tem 3,2 mm de lado e está imersa em um campo elétrico uniforme de módulo E = 1800 N/C e
com linhas de campo fazendo um ângulo de 35° com a normal, como mostra a figura.
Tome esta normal como apontando "para fora", como se a superfície fosse a tampa de uma caixa. Determine aproximadamente o fluxo elétrico em N.m2/C
através da superfície e considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .

-3,256
-8,36
-0,015
-0,789
-2,56
Três esferas com cargas de 2.10-6C, 7.10-6C e -4.10-6C são colocadas nos vértices de um triângulo equilátero, de 0,5 m de lado. Determinar aproximadamente a intensidade da força resultante sobre a esfera de 7.10-6C. Considere a constante eletrostática igual a 9.109 N.m²/c².

2,56 N
6,35 N
0,872 N
8,99 N
10 N
Em certa situação, temos uma placa não-condutora infinita que possui uma densidade superficial de cargas igual a +5,80 . 10-12C/m2.
Qual é aproximadamente o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga q = +1,6. 10-19C é deslocada
da superfície da placa para um ponto P situado a uma distância d = 3,56. 10-2m da superfície da placa?
considere a constante eletrostática igual a 8,99 × 109 N.m2/C2.
6.10-19 J
8.10-19 J
1,87.10-21 J
1,6.10-19 J
6.10-20 J
Determine o campo magnético em um ponto situado nas proximidades do centro de um solenóide longo de comprimento 15 cm e raio 2.50 cm e que possui 600 espiras enroladas de modo compacto. Sabendo que a corrente que passa nas espiras e igual a 8 A. Considere a permeabilidade igual a 4`pi.10-7`
0,0402 T
3 T
2 T
1,5 T
1,2 T
Determine aproximadamente intensidade de uma carga elétrica, sabendo que o campo elétrico a 50 cm de distância tem intensidade de 2N/C, considere a constante eletrostatica igual a 8, 99 · 109 Nm2/C2, sendo 1 pC = 10-12 C.
12 pC
56 pC
30 pC
40 pC
25 pC
Considere uma esfera condutora com 10 cm de raio. Sabendo que o campo elétrico a 15 cm do centro da esfera tem um módulo de 3 × 10 3 N/C e aponta para o centro da esfera, Determine aproximadamente a carga desta esfera. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
7,5 · 10-10 C
7,5 · 10-9 C
7,5 · 10-11 C
7,5 · 10-12 C
7,5 · 10-13 C
Calcule a força elétrica resultante na carga Q1= 6μC, localizada em P1(1, 2, –3), que sofre influência de Q2 = 13μC na posição P2(2 , – 4, 1) e Q3= -7μC na posição P3(3, –2,–2). Considere εr= 1,8.
Note que:

-3,256
-8,36
-0,015
-0,789
-2,56
Três esferas com cargas de 2.10-6C, 7.10-6C e -4.10-6C são colocadas nos vértices de um triângulo equilátero, de 0,5 m de lado. Determinar aproximadamente a intensidade da força resultante sobre a esfera de 7.10-6C. Considere a constante eletrostática igual a 9.109 N.m²/c².

2,56 N
6,35 N
0,872 N
8,99 N
10 N
Em certa situação, temos uma placa não-condutora infinita que possui uma densidade superficial de cargas igual a +5,80 . 10-12C/m2.
Qual é aproximadamente o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga q = +1,6. 10-19C é deslocada
da superfície da placa para um ponto P situado a uma distância d = 3,56. 10-2m da superfície da placa?
considere a constante eletrostática igual a 8,99 × 109 N.m2/C2.
6.10-19 J
8.10-19 J
1,87.10-21 J
1,6.10-19 J
6.10-20 J
Determine o campo magnético em um ponto situado nas proximidades do centro de um solenóide longo de comprimento 15 cm e raio 2.50 cm e que possui 600 espiras enroladas de modo compacto. Sabendo que a corrente que passa nas espiras e igual a 8 A. Considere a permeabilidade igual a 4`pi.10-7`
0,0402 T
3 T
2 T
1,5 T
1,2 T
Determine aproximadamente intensidade de uma carga elétrica, sabendo que o campo elétrico a 50 cm de distância tem intensidade de 2N/C, considere a constante eletrostatica igual a 8, 99 · 109 Nm2/C2, sendo 1 pC = 10-12 C.
12 pC
56 pC
30 pC
40 pC
25 pC
Considere uma esfera condutora com 10 cm de raio. Sabendo que o campo elétrico a 15 cm do centro da esfera tem um módulo de 3 × 10 3 N/C e aponta para o centro da esfera, Determine aproximadamente a carga desta esfera. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
7,5 · 10-10 C
7,5 · 10-9 C
7,5 · 10-11 C
7,5 · 10-12 C
7,5 · 10-13 C
Calcule a força elétrica resultante na carga Q1= 6μC, localizada em P1(1, 2, –3), que sofre influência de Q2 = 13μC na posição P2(2 , – 4, 1) e Q3= -7μC na posição P3(3, –2,–2). Considere εr= 1,8.
Note que:


2,56 N
6,35 N
0,872 N
8,99 N
10 N
Em certa situação, temos uma placa não-condutora infinita que possui uma densidade superficial de cargas igual a +5,80 . 10-12C/m2.
Qual é aproximadamente o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga q = +1,6. 10-19C é deslocada
da superfície da placa para um ponto P situado a uma distância d = 3,56. 10-2m da superfície da placa?
considere a constante eletrostática igual a 8,99 × 109 N.m2/C2.
6.10-19 J
8.10-19 J
1,87.10-21 J
1,6.10-19 J
6.10-20 J
Determine o campo magnético em um ponto situado nas proximidades do centro de um solenóide longo de comprimento 15 cm e raio 2.50 cm e que possui 600 espiras enroladas de modo compacto. Sabendo que a corrente que passa nas espiras e igual a 8 A. Considere a permeabilidade igual a 4`pi.10-7`
0,0402 T
3 T
2 T
1,5 T
1,2 T
Determine aproximadamente intensidade de uma carga elétrica, sabendo que o campo elétrico a 50 cm de distância tem intensidade de 2N/C, considere a constante eletrostatica igual a 8, 99 · 109 Nm2/C2, sendo 1 pC = 10-12 C.
12 pC
56 pC
30 pC
40 pC
25 pC
Considere uma esfera condutora com 10 cm de raio. Sabendo que o campo elétrico a 15 cm do centro da esfera tem um módulo de 3 × 10 3 N/C e aponta para o centro da esfera, Determine aproximadamente a carga desta esfera. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
7,5 · 10-10 C
7,5 · 10-9 C
7,5 · 10-11 C
7,5 · 10-12 C
7,5 · 10-13 C
Calcule a força elétrica resultante na carga Q1= 6μC, localizada em P1(1, 2, –3), que sofre influência de Q2 = 13μC na posição P2(2 , – 4, 1) e Q3= -7μC na posição P3(3, –2,–2). Considere εr= 1,8.
Note que:

6.10-19 J
8.10-19 J
1,87.10-21 J
1,6.10-19 J
6.10-20 J
Determine o campo magnético em um ponto situado nas proximidades do centro de um solenóide longo de comprimento 15 cm e raio 2.50 cm e que possui 600 espiras enroladas de modo compacto. Sabendo que a corrente que passa nas espiras e igual a 8 A. Considere a permeabilidade igual a 4`pi.10-7`
0,0402 T
3 T
2 T
1,5 T
1,2 T
Determine aproximadamente intensidade de uma carga elétrica, sabendo que o campo elétrico a 50 cm de distância tem intensidade de 2N/C, considere a constante eletrostatica igual a 8, 99 · 109 Nm2/C2, sendo 1 pC = 10-12 C.
12 pC
56 pC
30 pC
40 pC
25 pC
Considere uma esfera condutora com 10 cm de raio. Sabendo que o campo elétrico a 15 cm do centro da esfera tem um módulo de 3 × 10 3 N/C e aponta para o centro da esfera, Determine aproximadamente a carga desta esfera. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
7,5 · 10-10 C
7,5 · 10-9 C
7,5 · 10-11 C
7,5 · 10-12 C
7,5 · 10-13 C
Calcule a força elétrica resultante na carga Q1= 6μC, localizada em P1(1, 2, –3), que sofre influência de Q2 = 13μC na posição P2(2 , – 4, 1) e Q3= -7μC na posição P3(3, –2,–2). Considere εr= 1,8.
Note que:

0,0402 T
3 T
2 T
1,5 T
1,2 T
Determine aproximadamente intensidade de uma carga elétrica, sabendo que o campo elétrico a 50 cm de distância tem intensidade de 2N/C, considere a constante eletrostatica igual a 8, 99 · 109 Nm2/C2, sendo 1 pC = 10-12 C.
12 pC
56 pC
30 pC
40 pC
25 pC
Considere uma esfera condutora com 10 cm de raio. Sabendo que o campo elétrico a 15 cm do centro da esfera tem um módulo de 3 × 10 3 N/C e aponta para o centro da esfera, Determine aproximadamente a carga desta esfera. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
7,5 · 10-10 C
7,5 · 10-9 C
7,5 · 10-11 C
7,5 · 10-12 C
7,5 · 10-13 C
Calcule a força elétrica resultante na carga Q1= 6μC, localizada em P1(1, 2, –3), que sofre influência de Q2 = 13μC na posição P2(2 , – 4, 1) e Q3= -7μC na posição P3(3, –2,–2). Considere εr= 1,8.
Note que:

12 pC
56 pC
30 pC
40 pC
25 pC
Considere uma esfera condutora com 10 cm de raio. Sabendo que o campo elétrico a 15 cm do centro da esfera tem um módulo de 3 × 10 3 N/C e aponta para o centro da esfera, Determine aproximadamente a carga desta esfera. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
7,5 · 10-10 C
7,5 · 10-9 C
7,5 · 10-11 C
7,5 · 10-12 C
7,5 · 10-13 C
Calcule a força elétrica resultante na carga Q1= 6μC, localizada em P1(1, 2, –3), que sofre influência de Q2 = 13μC na posição P2(2 , – 4, 1) e Q3= -7μC na posição P3(3, –2,–2). Considere εr= 1,8.
Note que:

7,5 · 10-10 C
7,5 · 10-9 C
7,5 · 10-11 C
7,5 · 10-12 C
7,5 · 10-13 C