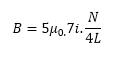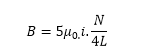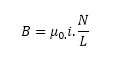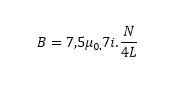ELETROMAGNETISMO
Determine aproximadamente a carga em excesso de uma esfera condutora de raio r = 0,15 m se o potencial da esfera é 1500 V e V = 0 no infinito? considere a constante eletrostática igual a 8,99.109 (SI)
2,5 · 10-8 C
2 · 10-6 C
5 · 10-7 C
4,5 · 10-7 C
7,5 · 10-5 C
Determine aproximadamente o raio da trajetória circular percorrida por uma partícula de carga elétrica igual 1,6.10-19 C e massa 9,11.10-31 kg e sujeita a um campo magnético de 0,5 T, e com uma velocidade de 3.107 m/s.
9,42.10 - 3 m
1,42.10 - 2 m
7,72.10 - 7 m
3,62.10 - 7 m
3,42.10 - 4 m
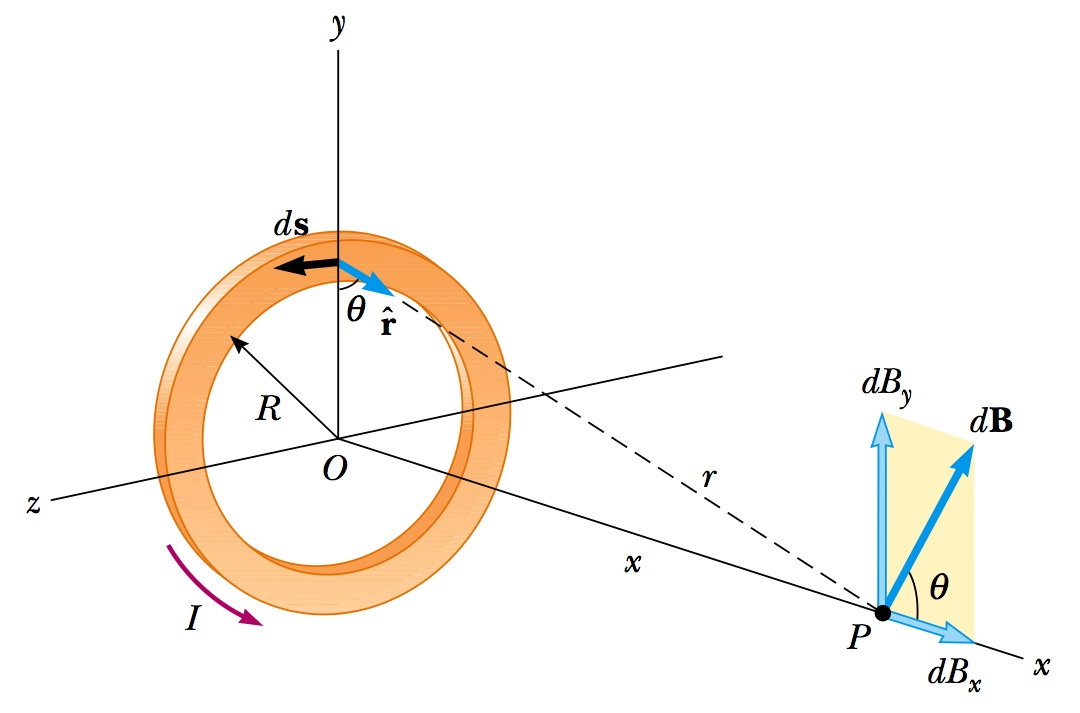
Considere um anel de fio circular de corrente ( i) , como na figura abaixo o campo magnético no ponto P no eixo x da espira devido a um elemento ds do fio e mostrada na mesma figura, Utilizando a lei de Biot-Savart, o campo magnético no centro do anel ( x = 0), produzido pela corrente no anel circular, pode ser dado por:
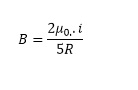
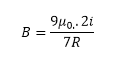
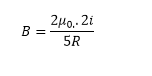
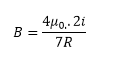
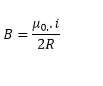
Considere o circuito mostrado na figura abaixo, que contem N espiras e comprimento L, com suas correntes atravessando o circuito. Usando a Lei de Ampere mostre que o campo magnético deste solenoide pode ser dado por:

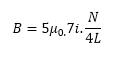
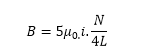
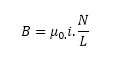

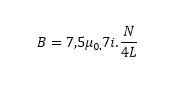
Qual é o valor da corrente da seguinte situação:
Uma barra horizontal com 0,2 m de comprimento é montada sobre uma balança e conduz uma corrente. No local da barra existe um campo magnético uniforme horizontal com módulo igual a 0,067 T e direção perpendicular à barra. A força magnética sobre a barra medida pela balança é igual a 0,13 N.
2,5 · 10-8 C
2 · 10-6 C
5 · 10-7 C
4,5 · 10-7 C
7,5 · 10-5 C
Determine aproximadamente o raio da trajetória circular percorrida por uma partícula de carga elétrica igual 1,6.10-19 C e massa 9,11.10-31 kg e sujeita a um campo magnético de 0,5 T, e com uma velocidade de 3.107 m/s.
9,42.10 - 3 m
1,42.10 - 2 m
7,72.10 - 7 m
3,62.10 - 7 m
3,42.10 - 4 m
Considere um anel de fio circular de corrente ( i) , como na figura abaixo o campo magnético no ponto P no eixo x da espira devido a um elemento ds do fio e mostrada na mesma figura, Utilizando a lei de Biot-Savart, o campo magnético no centro do anel ( x = 0), produzido pela corrente no anel circular, pode ser dado por:

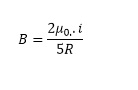
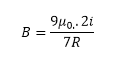
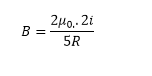
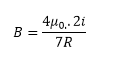
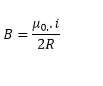
Considere o circuito mostrado na figura abaixo, que contem N espiras e comprimento L, com suas correntes atravessando o circuito. Usando a Lei de Ampere mostre que o campo magnético deste solenoide pode ser dado por:

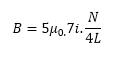
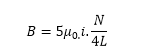
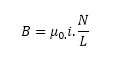

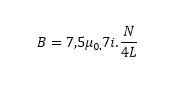
Qual é o valor da corrente da seguinte situação:
Uma barra horizontal com 0,2 m de comprimento é montada sobre uma balança e conduz uma corrente. No local da barra existe um campo magnético uniforme horizontal com módulo igual a 0,067 T e direção perpendicular à barra. A força magnética sobre a barra medida pela balança é igual a 0,13 N.
9,42.10 - 3 m
1,42.10 - 2 m
7,72.10 - 7 m
3,62.10 - 7 m
3,42.10 - 4 m
Considere um anel de fio circular de corrente ( i) , como na figura abaixo o campo magnético no ponto P no eixo x da espira devido a um elemento ds do fio e mostrada na mesma figura, Utilizando a lei de Biot-Savart, o campo magnético no centro do anel ( x = 0), produzido pela corrente no anel circular, pode ser dado por:

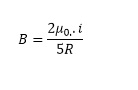
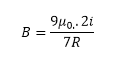
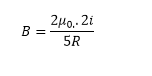
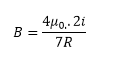
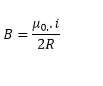
Considere o circuito mostrado na figura abaixo, que contem N espiras e comprimento L, com suas correntes atravessando o circuito. Usando a Lei de Ampere mostre que o campo magnético deste solenoide pode ser dado por:

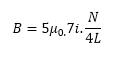
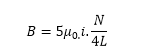
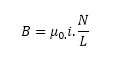

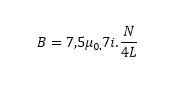
Qual é o valor da corrente da seguinte situação:
Uma barra horizontal com 0,2 m de comprimento é montada sobre uma balança e conduz uma corrente. No local da barra existe um campo magnético uniforme horizontal com módulo igual a 0,067 T e direção perpendicular à barra. A força magnética sobre a barra medida pela balança é igual a 0,13 N.

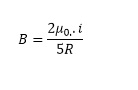
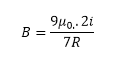
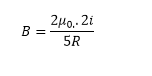
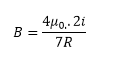
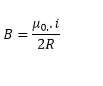
Considere o circuito mostrado na figura abaixo, que contem N espiras e comprimento L, com suas correntes atravessando o circuito. Usando a Lei de Ampere mostre que o campo magnético deste solenoide pode ser dado por:

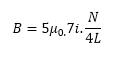
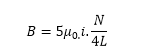
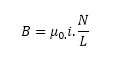

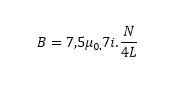
Qual é o valor da corrente da seguinte situação:
Uma barra horizontal com 0,2 m de comprimento é montada sobre uma balança e conduz uma corrente. No local da barra existe um campo magnético uniforme horizontal com módulo igual a 0,067 T e direção perpendicular à barra. A força magnética sobre a barra medida pela balança é igual a 0,13 N.