CIRCUITOS ELÉTRICOS III
Um circito RL série possui um resistor de 1Kohm e um indutor de 1mH, determine a sua constante de tempo.
10s
1s
100s
1ms
1us
Determine a contênte de tempo de um cicuito RC série o qual possui um resistor de 20Kohms em série com um capacitor de 1mf.
20ms
20 seg.
20 us
20 ps
20 ns
Um circuito RC série de primeira ordem apresenta uma tensão de entrada 4 V sendo um degrau unitário para t > 0 segundo, determine a tensão do resistor no tempo de 3 segundo(s). Sabendo que o capacitor é 3 mf e o resistor de 1 Kohms e seus valores iniciais iguais a zero.
-1.528 Volt(s)
5.886 Volt(s)
2.472 Volt(s)
0.368 Volt(s)
1.472 Volt(s)
Um circuito RC série de primeira ordem apresenta uma tensão de entrada 10 V sendo um degrau unitário para t > 0 segundo, determine a tensão do capacitor no tempo de 1 segundo(s). Sabendo que o capacitor é 2 mf e o resistor de 7 Kohms e seus valores iniciais iguais a zero.
0.230 Volt(s)
3.447 Volt(s)
0.689 Volt(s)
2.689 Volt(s)
-0.311 Volt(s)
Determine a transformada de laplace da EDO abaixo :
5 . dx(t)/dt+8 . x(t) = 7.
1.75 - 6.12 . exp(-5.60 . t)
1.88 - 3.88 . exp(-1.60 . t)
0.22 - 0.10 . exp(-5.60 . t)
0.88 - 0.88 . exp(-1.60 . t)
-1.12 - -9.12 . exp(-9.60 . t)
Determine a Transformada de Laplace de uma derivada apresentada abaixo.
F( t ) = dF( t )/dt
F( s ) = F( s ).s
F( s ) = F( s ).s - F( 0 )
F( s ) = F( 0 ).s - F( s )
F( s ) = F( 0 )/s - F( 0 )
F( s ) = F( 0 ) - F( s ).s
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 6 Kohms, indutor = 4 mH, capacitor = 3 mF.
Vc(s)/Vi(s)=1/( 12.00 u . s² + 18.00 . s + 1)
Vc(s)/Vi(s)=1/( 8.00 u . s² + 15.00 . s + 1)
Vc(s)/Vi(s)=1/( 17.00 u . s² + 24.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.40 u . s² + 3.60 . s + 1)
Vc(s)/Vi(s)=1/( 36.00 u . s² + 180.00 . s + 1)
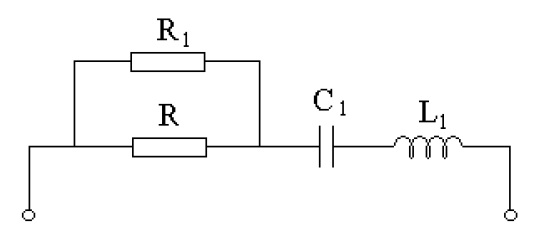
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 6 ohms , C1 = 5 F e L1 = 1 H.
4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.
10s
1s
100s
1ms
1us
Determine a contênte de tempo de um cicuito RC série o qual possui um resistor de 20Kohms em série com um capacitor de 1mf.
20ms
20 seg.
20 us
20 ps
20 ns
Um circuito RC série de primeira ordem apresenta uma tensão de entrada 4 V sendo um degrau unitário para t > 0 segundo, determine a tensão do resistor no tempo de 3 segundo(s). Sabendo que o capacitor é 3 mf e o resistor de 1 Kohms e seus valores iniciais iguais a zero.
-1.528 Volt(s)
5.886 Volt(s)
2.472 Volt(s)
0.368 Volt(s)
1.472 Volt(s)
Um circuito RC série de primeira ordem apresenta uma tensão de entrada 10 V sendo um degrau unitário para t > 0 segundo, determine a tensão do capacitor no tempo de 1 segundo(s). Sabendo que o capacitor é 2 mf e o resistor de 7 Kohms e seus valores iniciais iguais a zero.
0.230 Volt(s)
3.447 Volt(s)
0.689 Volt(s)
2.689 Volt(s)
-0.311 Volt(s)
Determine a transformada de laplace da EDO abaixo :
5 . dx(t)/dt+8 . x(t) = 7.
1.75 - 6.12 . exp(-5.60 . t)
1.88 - 3.88 . exp(-1.60 . t)
0.22 - 0.10 . exp(-5.60 . t)
0.88 - 0.88 . exp(-1.60 . t)
-1.12 - -9.12 . exp(-9.60 . t)
Determine a Transformada de Laplace de uma derivada apresentada abaixo.
F( t ) = dF( t )/dt
F( s ) = F( s ).s
F( s ) = F( s ).s - F( 0 )
F( s ) = F( 0 ).s - F( s )
F( s ) = F( 0 )/s - F( 0 )
F( s ) = F( 0 ) - F( s ).s
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 6 Kohms, indutor = 4 mH, capacitor = 3 mF.
Vc(s)/Vi(s)=1/( 12.00 u . s² + 18.00 . s + 1)
Vc(s)/Vi(s)=1/( 8.00 u . s² + 15.00 . s + 1)
Vc(s)/Vi(s)=1/( 17.00 u . s² + 24.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.40 u . s² + 3.60 . s + 1)
Vc(s)/Vi(s)=1/( 36.00 u . s² + 180.00 . s + 1)
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 6 ohms , C1 = 5 F e L1 = 1 H.

4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.
20ms
20 seg.
20 us
20 ps
20 ns
Um circuito RC série de primeira ordem apresenta uma tensão de entrada 4 V sendo um degrau unitário para t > 0 segundo, determine a tensão do resistor no tempo de 3 segundo(s). Sabendo que o capacitor é 3 mf e o resistor de 1 Kohms e seus valores iniciais iguais a zero.
-1.528 Volt(s)
5.886 Volt(s)
2.472 Volt(s)
0.368 Volt(s)
1.472 Volt(s)
Um circuito RC série de primeira ordem apresenta uma tensão de entrada 10 V sendo um degrau unitário para t > 0 segundo, determine a tensão do capacitor no tempo de 1 segundo(s). Sabendo que o capacitor é 2 mf e o resistor de 7 Kohms e seus valores iniciais iguais a zero.
0.230 Volt(s)
3.447 Volt(s)
0.689 Volt(s)
2.689 Volt(s)
-0.311 Volt(s)
Determine a transformada de laplace da EDO abaixo :
5 . dx(t)/dt+8 . x(t) = 7.
1.75 - 6.12 . exp(-5.60 . t)
1.88 - 3.88 . exp(-1.60 . t)
0.22 - 0.10 . exp(-5.60 . t)
0.88 - 0.88 . exp(-1.60 . t)
-1.12 - -9.12 . exp(-9.60 . t)
Determine a Transformada de Laplace de uma derivada apresentada abaixo.
F( t ) = dF( t )/dt
F( s ) = F( s ).s
F( s ) = F( s ).s - F( 0 )
F( s ) = F( 0 ).s - F( s )
F( s ) = F( 0 )/s - F( 0 )
F( s ) = F( 0 ) - F( s ).s
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 6 Kohms, indutor = 4 mH, capacitor = 3 mF.
Vc(s)/Vi(s)=1/( 12.00 u . s² + 18.00 . s + 1)
Vc(s)/Vi(s)=1/( 8.00 u . s² + 15.00 . s + 1)
Vc(s)/Vi(s)=1/( 17.00 u . s² + 24.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.40 u . s² + 3.60 . s + 1)
Vc(s)/Vi(s)=1/( 36.00 u . s² + 180.00 . s + 1)
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 6 ohms , C1 = 5 F e L1 = 1 H.

4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.
-1.528 Volt(s)
5.886 Volt(s)
2.472 Volt(s)
0.368 Volt(s)
1.472 Volt(s)
Um circuito RC série de primeira ordem apresenta uma tensão de entrada 10 V sendo um degrau unitário para t > 0 segundo, determine a tensão do capacitor no tempo de 1 segundo(s). Sabendo que o capacitor é 2 mf e o resistor de 7 Kohms e seus valores iniciais iguais a zero.
0.230 Volt(s)
3.447 Volt(s)
0.689 Volt(s)
2.689 Volt(s)
-0.311 Volt(s)
Determine a transformada de laplace da EDO abaixo :
5 . dx(t)/dt+8 . x(t) = 7.
1.75 - 6.12 . exp(-5.60 . t)
1.88 - 3.88 . exp(-1.60 . t)
0.22 - 0.10 . exp(-5.60 . t)
0.88 - 0.88 . exp(-1.60 . t)
-1.12 - -9.12 . exp(-9.60 . t)
Determine a Transformada de Laplace de uma derivada apresentada abaixo.
F( t ) = dF( t )/dt
F( s ) = F( s ).s
F( s ) = F( s ).s - F( 0 )
F( s ) = F( 0 ).s - F( s )
F( s ) = F( 0 )/s - F( 0 )
F( s ) = F( 0 ) - F( s ).s
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 6 Kohms, indutor = 4 mH, capacitor = 3 mF.
Vc(s)/Vi(s)=1/( 12.00 u . s² + 18.00 . s + 1)
Vc(s)/Vi(s)=1/( 8.00 u . s² + 15.00 . s + 1)
Vc(s)/Vi(s)=1/( 17.00 u . s² + 24.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.40 u . s² + 3.60 . s + 1)
Vc(s)/Vi(s)=1/( 36.00 u . s² + 180.00 . s + 1)
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 6 ohms , C1 = 5 F e L1 = 1 H.

4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.
0.230 Volt(s)
3.447 Volt(s)
0.689 Volt(s)
2.689 Volt(s)
-0.311 Volt(s)
Determine a transformada de laplace da EDO abaixo :
5 . dx(t)/dt+8 . x(t) = 7.
1.75 - 6.12 . exp(-5.60 . t)
1.88 - 3.88 . exp(-1.60 . t)
0.22 - 0.10 . exp(-5.60 . t)
0.88 - 0.88 . exp(-1.60 . t)
-1.12 - -9.12 . exp(-9.60 . t)
Determine a Transformada de Laplace de uma derivada apresentada abaixo.
F( t ) = dF( t )/dt
F( s ) = F( s ).s
F( s ) = F( s ).s - F( 0 )
F( s ) = F( 0 ).s - F( s )
F( s ) = F( 0 )/s - F( 0 )
F( s ) = F( 0 ) - F( s ).s
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 6 Kohms, indutor = 4 mH, capacitor = 3 mF.
Vc(s)/Vi(s)=1/( 12.00 u . s² + 18.00 . s + 1)
Vc(s)/Vi(s)=1/( 8.00 u . s² + 15.00 . s + 1)
Vc(s)/Vi(s)=1/( 17.00 u . s² + 24.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.40 u . s² + 3.60 . s + 1)
Vc(s)/Vi(s)=1/( 36.00 u . s² + 180.00 . s + 1)
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 6 ohms , C1 = 5 F e L1 = 1 H.

4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.
5 . dx(t)/dt+8 . x(t) = 7.
1.75 - 6.12 . exp(-5.60 . t)
1.88 - 3.88 . exp(-1.60 . t)
0.22 - 0.10 . exp(-5.60 . t)
0.88 - 0.88 . exp(-1.60 . t)
-1.12 - -9.12 . exp(-9.60 . t)
Determine a Transformada de Laplace de uma derivada apresentada abaixo.
F( t ) = dF( t )/dt
F( s ) = F( s ).s
F( s ) = F( s ).s - F( 0 )
F( s ) = F( 0 ).s - F( s )
F( s ) = F( 0 )/s - F( 0 )
F( s ) = F( 0 ) - F( s ).s
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 6 Kohms, indutor = 4 mH, capacitor = 3 mF.
Vc(s)/Vi(s)=1/( 12.00 u . s² + 18.00 . s + 1)
Vc(s)/Vi(s)=1/( 8.00 u . s² + 15.00 . s + 1)
Vc(s)/Vi(s)=1/( 17.00 u . s² + 24.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.40 u . s² + 3.60 . s + 1)
Vc(s)/Vi(s)=1/( 36.00 u . s² + 180.00 . s + 1)
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 6 ohms , C1 = 5 F e L1 = 1 H.

4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.
F( t ) = dF( t )/dt
F( s ) = F( s ).s
F( s ) = F( s ).s - F( 0 )
F( s ) = F( 0 ).s - F( s )
F( s ) = F( 0 )/s - F( 0 )
F( s ) = F( 0 ) - F( s ).s
Determine a função de transferência que relaciona a tensão de entrada Vi(t) com a tensão do capacitor Vc(s) de um circuito série de 2° ordem série, sabendo que o resistor é igual a 6 Kohms, indutor = 4 mH, capacitor = 3 mF.
Vc(s)/Vi(s)=1/( 12.00 u . s² + 18.00 . s + 1)
Vc(s)/Vi(s)=1/( 8.00 u . s² + 15.00 . s + 1)
Vc(s)/Vi(s)=1/( 17.00 u . s² + 24.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.40 u . s² + 3.60 . s + 1)
Vc(s)/Vi(s)=1/( 36.00 u . s² + 180.00 . s + 1)
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 6 ohms , C1 = 5 F e L1 = 1 H.

4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.
Vc(s)/Vi(s)=1/( 12.00 u . s² + 18.00 . s + 1)
Vc(s)/Vi(s)=1/( 8.00 u . s² + 15.00 . s + 1)
Vc(s)/Vi(s)=1/( 17.00 u . s² + 24.00 . s + 1)
Vc(s)/Vi(s)=1/( 2.40 u . s² + 3.60 . s + 1)
Vc(s)/Vi(s)=1/( 36.00 u . s² + 180.00 . s + 1)
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 6 ohms , C1 = 5 F e L1 = 1 H.

4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.

4.05 ohms
-2.95 ohms
0.35 ohms
3.15 ohms
1.05 ohms
O circuito série RCL possui seus componentes com os seguintes valores C = 7 F, L= 9 H e R = 8 ohms, determine a sua frequência natural ou de ressonância wo.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo
O circuito série RCL possui C = 7 F, L= 3 H e R = 2 ohms, considerando que no instante t=0 segundos a fonte (9 V) ligada em série é acionada, determine o valor da tenção no indutor no instante em que a fonte é acionada.
-4.87 radianos / segundo
1.13 radianos / segundo
0.13 radianos / segundo
0.25 radianos / segundo
0.03 radianos / segundo