CIRCUITOS ELÉTRICOS III
Um circuito RC série encontra-se com o capacitor inicialmente carregado com uma tensão de 5 V, sabe-se que o valor do capacitor é de 5 mF e o valor do resistor é igual á 1 Khons. Determine o valor da tensão no capacitor quando o tempo de descarregamento está em 3 segundos.
2.74 Volt(s)
0.26 Volt(s)
2.26 Volt(s)
0.74 Volt(s)
3.74 Volt(s)
O circuito série RCL abaixo apresenta C = 6 F, L= 2 H e R = 5 ohms, considerando que no instante t=0 segundos a fonte (8 V) é acionada, determine o valor da tensção no indutor no instante em que a fonte é acionada.
VL(0)=8.00 V
VL(0)=3.00 V
VL(0)=4.00 V
VL(0)=12.00 V
VL(0)=40.00 V
Determine o valor do tal para um circuito que apresenta a seguinte função a exitação zero Vc(t) = 12*exp(-1/tal*t), sabe-se que a tenção do capacitor no tempo de 13 segundos é igual a metade do valor inicial.
19.76
22.76
18.76
14.76
16.76
Determine o valor do tal para um circuito que apresenta a seguinte função a exitação zero Vc(t) = 18*exp(-1/tal*t), sabe-se que a tenção do capacitor no tempo de 25 segundos é igual a metade do valor inicial.
36.07
32.07
38.07
40.07
35.07
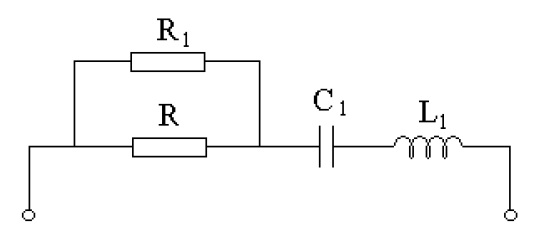
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 4 ohms , C1 = 4 F e L1 = 2 H.
4.19 ohms
1.09 ohms
2.19 ohms
-2.81 ohms
10.94 ohms
Dada a função no tempo F(t) = 2 . t³ . exp(-10 . t), determine a sua transformada de Laplace.
24/(s + 20)^4
12/(s + 10)^4
13/(s + 20)^4
3/(s + 1)^4
10/(s + 1)^4
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 11 . t² + 6, determine a sua transformada de Laplace.
(18 + 2 . s²)/s³
(20 + 4 . s²)/s³
(27 + 11 . s²)/s³
(23 + 7 . s²)/s³
(22 + 6 . s²)/s³
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 5 . t² + 7, determine a sua transformada de Laplace.
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6
2.74 Volt(s)
0.26 Volt(s)
2.26 Volt(s)
0.74 Volt(s)
3.74 Volt(s)
O circuito série RCL abaixo apresenta C = 6 F, L= 2 H e R = 5 ohms, considerando que no instante t=0 segundos a fonte (8 V) é acionada, determine o valor da tensção no indutor no instante em que a fonte é acionada.
VL(0)=8.00 V
VL(0)=3.00 V
VL(0)=4.00 V
VL(0)=12.00 V
VL(0)=40.00 V
Determine o valor do tal para um circuito que apresenta a seguinte função a exitação zero Vc(t) = 12*exp(-1/tal*t), sabe-se que a tenção do capacitor no tempo de 13 segundos é igual a metade do valor inicial.
19.76
22.76
18.76
14.76
16.76
Determine o valor do tal para um circuito que apresenta a seguinte função a exitação zero Vc(t) = 18*exp(-1/tal*t), sabe-se que a tenção do capacitor no tempo de 25 segundos é igual a metade do valor inicial.
36.07
32.07
38.07
40.07
35.07
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 4 ohms , C1 = 4 F e L1 = 2 H.

4.19 ohms
1.09 ohms
2.19 ohms
-2.81 ohms
10.94 ohms
Dada a função no tempo F(t) = 2 . t³ . exp(-10 . t), determine a sua transformada de Laplace.
24/(s + 20)^4
12/(s + 10)^4
13/(s + 20)^4
3/(s + 1)^4
10/(s + 1)^4
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 11 . t² + 6, determine a sua transformada de Laplace.
(18 + 2 . s²)/s³
(20 + 4 . s²)/s³
(27 + 11 . s²)/s³
(23 + 7 . s²)/s³
(22 + 6 . s²)/s³
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 5 . t² + 7, determine a sua transformada de Laplace.
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6
VL(0)=8.00 V
VL(0)=3.00 V
VL(0)=4.00 V
VL(0)=12.00 V
VL(0)=40.00 V
Determine o valor do tal para um circuito que apresenta a seguinte função a exitação zero Vc(t) = 12*exp(-1/tal*t), sabe-se que a tenção do capacitor no tempo de 13 segundos é igual a metade do valor inicial.
19.76
22.76
18.76
14.76
16.76
Determine o valor do tal para um circuito que apresenta a seguinte função a exitação zero Vc(t) = 18*exp(-1/tal*t), sabe-se que a tenção do capacitor no tempo de 25 segundos é igual a metade do valor inicial.
36.07
32.07
38.07
40.07
35.07
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 4 ohms , C1 = 4 F e L1 = 2 H.

4.19 ohms
1.09 ohms
2.19 ohms
-2.81 ohms
10.94 ohms
Dada a função no tempo F(t) = 2 . t³ . exp(-10 . t), determine a sua transformada de Laplace.
24/(s + 20)^4
12/(s + 10)^4
13/(s + 20)^4
3/(s + 1)^4
10/(s + 1)^4
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 11 . t² + 6, determine a sua transformada de Laplace.
(18 + 2 . s²)/s³
(20 + 4 . s²)/s³
(27 + 11 . s²)/s³
(23 + 7 . s²)/s³
(22 + 6 . s²)/s³
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 5 . t² + 7, determine a sua transformada de Laplace.
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6
19.76
22.76
18.76
14.76
16.76
Determine o valor do tal para um circuito que apresenta a seguinte função a exitação zero Vc(t) = 18*exp(-1/tal*t), sabe-se que a tenção do capacitor no tempo de 25 segundos é igual a metade do valor inicial.
36.07
32.07
38.07
40.07
35.07
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 4 ohms , C1 = 4 F e L1 = 2 H.

4.19 ohms
1.09 ohms
2.19 ohms
-2.81 ohms
10.94 ohms
Dada a função no tempo F(t) = 2 . t³ . exp(-10 . t), determine a sua transformada de Laplace.
24/(s + 20)^4
12/(s + 10)^4
13/(s + 20)^4
3/(s + 1)^4
10/(s + 1)^4
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 11 . t² + 6, determine a sua transformada de Laplace.
(18 + 2 . s²)/s³
(20 + 4 . s²)/s³
(27 + 11 . s²)/s³
(23 + 7 . s²)/s³
(22 + 6 . s²)/s³
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 5 . t² + 7, determine a sua transformada de Laplace.
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6
36.07
32.07
38.07
40.07
35.07
Para o circuito da figura abaixo, calcule o valor de R necessário para uma resposta com com amortecimento crítico. Considere R1 = 4 ohms , C1 = 4 F e L1 = 2 H.

4.19 ohms
1.09 ohms
2.19 ohms
-2.81 ohms
10.94 ohms
Dada a função no tempo F(t) = 2 . t³ . exp(-10 . t), determine a sua transformada de Laplace.
24/(s + 20)^4
12/(s + 10)^4
13/(s + 20)^4
3/(s + 1)^4
10/(s + 1)^4
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 11 . t² + 6, determine a sua transformada de Laplace.
(18 + 2 . s²)/s³
(20 + 4 . s²)/s³
(27 + 11 . s²)/s³
(23 + 7 . s²)/s³
(22 + 6 . s²)/s³
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 5 . t² + 7, determine a sua transformada de Laplace.
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6

4.19 ohms
1.09 ohms
2.19 ohms
-2.81 ohms
10.94 ohms
Dada a função no tempo F(t) = 2 . t³ . exp(-10 . t), determine a sua transformada de Laplace.
24/(s + 20)^4
12/(s + 10)^4
13/(s + 20)^4
3/(s + 1)^4
10/(s + 1)^4
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 11 . t² + 6, determine a sua transformada de Laplace.
(18 + 2 . s²)/s³
(20 + 4 . s²)/s³
(27 + 11 . s²)/s³
(23 + 7 . s²)/s³
(22 + 6 . s²)/s³
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 5 . t² + 7, determine a sua transformada de Laplace.
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6
24/(s + 20)^4
12/(s + 10)^4
13/(s + 20)^4
3/(s + 1)^4
10/(s + 1)^4
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 11 . t² + 6, determine a sua transformada de Laplace.
(18 + 2 . s²)/s³
(20 + 4 . s²)/s³
(27 + 11 . s²)/s³
(23 + 7 . s²)/s³
(22 + 6 . s²)/s³
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 5 . t² + 7, determine a sua transformada de Laplace.
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6
(18 + 2 . s²)/s³
(20 + 4 . s²)/s³
(27 + 11 . s²)/s³
(23 + 7 . s²)/s³
(22 + 6 . s²)/s³
A transformada de Laplace é um método matemático que translada uma função no domínio do tempo para o domínio da frequencia, dada a função F(t) = 5 . t² + 7, determine a sua transformada de Laplace.
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6
F(s)=(6 + 3 . s²)/s³
F(s)=(10 + 7 . s²)/s³
F(s)=(12 + 9 . s²)/s³
F(s)=(15 + 12 . s²)/s³
F(s)=(8 + 5 . s²)/s³
Dado um circuito RC ( resistor e capacitor ) série, no tempo t=0 segundos, fonte de tensão de 1 V é acoplada ao circuito causando o carregamento do capacitor, determine no instante de 6 segundos. ( Sabemos : C = 2 mF, R = 10 Kohm(s), considere todos os valores iniciais iguais a zero )
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA
Dada a EDO abaixo, de um sistema L.I.T, determine a sua transformada de Laplace. (onde x(0) = 9)
1 . dx(t)/dt + 1 . x(t) = 6
- O valor da tensão no capacitor.
- O valor da tensão no resistor.
- O valor da corrente total.
V(capacitor) = 0.78 V ,V(resistor) = 2.22 V e I(total) = 5.07 mA
V(capacitor) = -1.74 V ,V(resistor) = -5.26 V e I(total) = 5.07 mA
V(capacitor) = 0.09 V ,V(resistor) = 0.09 V e I(total) = 5.07 mA
V(capacitor) = 3.26 V ,V(resistor) = 9.74 V e I(total) = 0.07 mA
V(capacitor) = 0.26 V ,V(resistor) = 0.74 V e I(total) = 0.07 mA