CIRCUITOS ELÉTRICOS II
A figura abaixo mostra o circuito equivalente monofásico de um sistema trifásico, sequência de fases ABC, a três condutores, que alimenta duas cargas, (1) e (2). Equacionando o circuito pode-se afirmar:
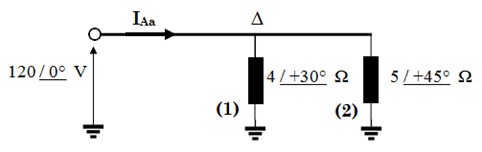
A reatância indutiva da carga (1) é igual a 2 â¦.
O defasamento da corrente que circula pela fase C do sistema é menor que 80°.
O valor, em módulo, da corrente que circula pela impedância ZAB da carga (1) é maior que 17 A.
O valor do módulo da tensão de linha na carga (2) é maior que 220 V.
O valor do módulo da corrente na linha B é menor que 50 A.
Uma fonte trifásica equilibrada, com tensão de linha igual a 240 V eficazes, fornece 8 kVA com fator de potência igual a 0,6 atrasado, para duas cargas ligadas em estrela, em paralelo. Sabendo que uma das cargas absorve 3 kW com fator de potência unitário e que a linha não possui impedância, pode-se afirmar que:
O valor do módulo da impedância da carga desconhecida é maior que 9 Ω.
O valor, em módulo, da corrente na linha é maior que 19 A.
O valor, em módulo, da corrente de fase da carga conhecida é menor que 7 A.
O fator de potência da segunda carga é igual a 0,6, atrasado.
O reativo total absorvido pela carga desconhecida é maior que 6,5 kVAr.
Uma carga equilibrada, ligada em triângulo, absorve 5 kW de um sistema trifásico cuja tensão eficaz da linha é igual a 400 V. Sendo o fator de potência da carga igual a 0,8, atrasado, é correto afirmar:
Se as três impedâncias da carga fossem ligadas em estrela o valor da potência aparente total absorvida seria igual a 1/3 do valor da ligação em triângulo.
O valor do módulo da corrente de fase na carga é menor que 5,0 A.
O valor da resistência da impedância é menor que 60 Ω.
A potência aparente trifásica absorvida pela carga é maior que 6,5 kVA.
O valor, em módulo, da queda de tensão sobre a indutância da impedância é maior que 250 V.
Um aluno encontrou uma bobina e quis determinar o valor de sua resistência interna Rbob e de sua indutância Lbob. Para tanto, conectou em série com a bobina uma resistência Rs = 10 Ω. Ele ligou o conjunto num varivolt e aplicou nele uma tensão de 36 V, eficazes, em 60 Hz. Com um voltímetro, mediu a tensão sobre o resistor, obtendo Vs = 20 V e sobre a bobina, obtendo Vbob = 22,4 V. Com os resultados obtidos fez os cálculos e concluiu que:
A tensão fasorial do varivolt deve ser escrita como Vvar = 36 /+40° V.
A bobina possui uma indutância menor que 30 mH.
A resistência da bobina é maior que 8 Ω.
A potência dissipada pelo resistor Rs é igual a 50 W.
Adotando a tensão Vs como referência, o ângulo da impedância da bobina é menor que 60°.
Determine o valor de YT.

Assinale a alternativa que corresponde a reposta.
YT=1,567 S< -50,194°
YT=0,195 S< -50,194°
YT=10,65 S< -45,65°
YT=1,567 S< +50,194°
YT=0,195 S< +50,194°
Seja o circuito paralelo mostrado na figura. A corrente fornecida pela fonte é dada por ig(t) = 5. cos (8.105 t) A. Equacionando o circuito é correto afirmar:
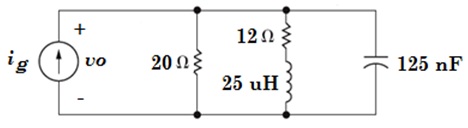
A corrente que circula pelo capacitor está adiantada da corrente da fonte de um ângulo maior que 50°.
A susceptância equivalente do circuito é indutiva e tem valor maior que 0,08 s.
Na construção do circuito equivalente, o valor da resistência equivalente é menor que 5,0 Ω.
A tensão instantânea, de regime permanente, sobre o indutor é dada por vL(t) = 44,76 cos (8.105 t - 10,2°) V.
O valor, do módulo, da tensão vo é menor que 50 V.
A figura mostra um resistor R = 2 Ω ligado em série com uma impedância Z, desconhecida. Do circuito sabe-se que o fator de potência é atrasado e que a potência média absorvida P = 300 W. É correto afirmar que:
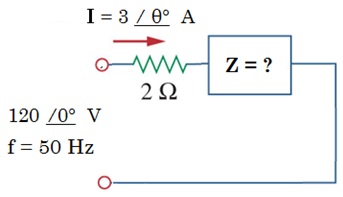
A queda de tensão fasorial sobre a impedância tem módulo menor que 110 V.
A impedância Z é composta por um único elemento, resistivo, de valor igual a 31,3 Ω.
A potência aparente absorvida pela impedância Z é maior que 400 VA.
A impedância Z pode ser composta por dois, ou mais elementos, ligados em série ou em paralelo.
O ângulo θ° da corrente é negativo e menor que 32°.
Uma carga, com impedância Zc, absorve de uma fonte de tensão senoidal de 120 V, eficazes, 12 kVA, com fator de potência 0,856. Para a carga, é correto afirmar que:
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.
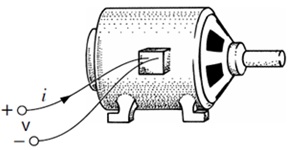
Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.

A reatância indutiva da carga (1) é igual a 2 â¦.
O defasamento da corrente que circula pela fase C do sistema é menor que 80°.
O valor, em módulo, da corrente que circula pela impedância ZAB da carga (1) é maior que 17 A.
O valor do módulo da tensão de linha na carga (2) é maior que 220 V.
O valor do módulo da corrente na linha B é menor que 50 A.
Uma fonte trifásica equilibrada, com tensão de linha igual a 240 V eficazes, fornece 8 kVA com fator de potência igual a 0,6 atrasado, para duas cargas ligadas em estrela, em paralelo. Sabendo que uma das cargas absorve 3 kW com fator de potência unitário e que a linha não possui impedância, pode-se afirmar que:
O valor do módulo da impedância da carga desconhecida é maior que 9 Ω.
O valor, em módulo, da corrente na linha é maior que 19 A.
O valor, em módulo, da corrente de fase da carga conhecida é menor que 7 A.
O fator de potência da segunda carga é igual a 0,6, atrasado.
O reativo total absorvido pela carga desconhecida é maior que 6,5 kVAr.
Uma carga equilibrada, ligada em triângulo, absorve 5 kW de um sistema trifásico cuja tensão eficaz da linha é igual a 400 V. Sendo o fator de potência da carga igual a 0,8, atrasado, é correto afirmar:
Se as três impedâncias da carga fossem ligadas em estrela o valor da potência aparente total absorvida seria igual a 1/3 do valor da ligação em triângulo.
O valor do módulo da corrente de fase na carga é menor que 5,0 A.
O valor da resistência da impedância é menor que 60 Ω.
A potência aparente trifásica absorvida pela carga é maior que 6,5 kVA.
O valor, em módulo, da queda de tensão sobre a indutância da impedância é maior que 250 V.
Um aluno encontrou uma bobina e quis determinar o valor de sua resistência interna Rbob e de sua indutância Lbob. Para tanto, conectou em série com a bobina uma resistência Rs = 10 Ω. Ele ligou o conjunto num varivolt e aplicou nele uma tensão de 36 V, eficazes, em 60 Hz. Com um voltímetro, mediu a tensão sobre o resistor, obtendo Vs = 20 V e sobre a bobina, obtendo Vbob = 22,4 V. Com os resultados obtidos fez os cálculos e concluiu que:
A tensão fasorial do varivolt deve ser escrita como Vvar = 36 /+40° V.
A bobina possui uma indutância menor que 30 mH.
A resistência da bobina é maior que 8 Ω.
A potência dissipada pelo resistor Rs é igual a 50 W.
Adotando a tensão Vs como referência, o ângulo da impedância da bobina é menor que 60°.
Determine o valor de YT.

Assinale a alternativa que corresponde a reposta.
YT=1,567 S< -50,194°
YT=0,195 S< -50,194°
YT=10,65 S< -45,65°
YT=1,567 S< +50,194°
YT=0,195 S< +50,194°
Seja o circuito paralelo mostrado na figura. A corrente fornecida pela fonte é dada por ig(t) = 5. cos (8.105 t) A. Equacionando o circuito é correto afirmar:

A corrente que circula pelo capacitor está adiantada da corrente da fonte de um ângulo maior que 50°.
A susceptância equivalente do circuito é indutiva e tem valor maior que 0,08 s.
Na construção do circuito equivalente, o valor da resistência equivalente é menor que 5,0 Ω.
A tensão instantânea, de regime permanente, sobre o indutor é dada por vL(t) = 44,76 cos (8.105 t - 10,2°) V.
O valor, do módulo, da tensão vo é menor que 50 V.
A figura mostra um resistor R = 2 Ω ligado em série com uma impedância Z, desconhecida. Do circuito sabe-se que o fator de potência é atrasado e que a potência média absorvida P = 300 W. É correto afirmar que:

A queda de tensão fasorial sobre a impedância tem módulo menor que 110 V.
A impedância Z é composta por um único elemento, resistivo, de valor igual a 31,3 Ω.
A potência aparente absorvida pela impedância Z é maior que 400 VA.
A impedância Z pode ser composta por dois, ou mais elementos, ligados em série ou em paralelo.
O ângulo θ° da corrente é negativo e menor que 32°.
Uma carga, com impedância Zc, absorve de uma fonte de tensão senoidal de 120 V, eficazes, 12 kVA, com fator de potência 0,856. Para a carga, é correto afirmar que:
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.
O valor do módulo da impedância da carga desconhecida é maior que 9 Ω.
O valor, em módulo, da corrente na linha é maior que 19 A.
O valor, em módulo, da corrente de fase da carga conhecida é menor que 7 A.
O fator de potência da segunda carga é igual a 0,6, atrasado.
O reativo total absorvido pela carga desconhecida é maior que 6,5 kVAr.
Uma carga equilibrada, ligada em triângulo, absorve 5 kW de um sistema trifásico cuja tensão eficaz da linha é igual a 400 V. Sendo o fator de potência da carga igual a 0,8, atrasado, é correto afirmar:
Se as três impedâncias da carga fossem ligadas em estrela o valor da potência aparente total absorvida seria igual a 1/3 do valor da ligação em triângulo.
O valor do módulo da corrente de fase na carga é menor que 5,0 A.
O valor da resistência da impedância é menor que 60 Ω.
A potência aparente trifásica absorvida pela carga é maior que 6,5 kVA.
O valor, em módulo, da queda de tensão sobre a indutância da impedância é maior que 250 V.
Um aluno encontrou uma bobina e quis determinar o valor de sua resistência interna Rbob e de sua indutância Lbob. Para tanto, conectou em série com a bobina uma resistência Rs = 10 Ω. Ele ligou o conjunto num varivolt e aplicou nele uma tensão de 36 V, eficazes, em 60 Hz. Com um voltímetro, mediu a tensão sobre o resistor, obtendo Vs = 20 V e sobre a bobina, obtendo Vbob = 22,4 V. Com os resultados obtidos fez os cálculos e concluiu que:
A tensão fasorial do varivolt deve ser escrita como Vvar = 36 /+40° V.
A bobina possui uma indutância menor que 30 mH.
A resistência da bobina é maior que 8 Ω.
A potência dissipada pelo resistor Rs é igual a 50 W.
Adotando a tensão Vs como referência, o ângulo da impedância da bobina é menor que 60°.
Determine o valor de YT.

Assinale a alternativa que corresponde a reposta.
YT=1,567 S< -50,194°
YT=0,195 S< -50,194°
YT=10,65 S< -45,65°
YT=1,567 S< +50,194°
YT=0,195 S< +50,194°
Seja o circuito paralelo mostrado na figura. A corrente fornecida pela fonte é dada por ig(t) = 5. cos (8.105 t) A. Equacionando o circuito é correto afirmar:

A corrente que circula pelo capacitor está adiantada da corrente da fonte de um ângulo maior que 50°.
A susceptância equivalente do circuito é indutiva e tem valor maior que 0,08 s.
Na construção do circuito equivalente, o valor da resistência equivalente é menor que 5,0 Ω.
A tensão instantânea, de regime permanente, sobre o indutor é dada por vL(t) = 44,76 cos (8.105 t - 10,2°) V.
O valor, do módulo, da tensão vo é menor que 50 V.
A figura mostra um resistor R = 2 Ω ligado em série com uma impedância Z, desconhecida. Do circuito sabe-se que o fator de potência é atrasado e que a potência média absorvida P = 300 W. É correto afirmar que:

A queda de tensão fasorial sobre a impedância tem módulo menor que 110 V.
A impedância Z é composta por um único elemento, resistivo, de valor igual a 31,3 Ω.
A potência aparente absorvida pela impedância Z é maior que 400 VA.
A impedância Z pode ser composta por dois, ou mais elementos, ligados em série ou em paralelo.
O ângulo θ° da corrente é negativo e menor que 32°.
Uma carga, com impedância Zc, absorve de uma fonte de tensão senoidal de 120 V, eficazes, 12 kVA, com fator de potência 0,856. Para a carga, é correto afirmar que:
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.
Se as três impedâncias da carga fossem ligadas em estrela o valor da potência aparente total absorvida seria igual a 1/3 do valor da ligação em triângulo.
O valor do módulo da corrente de fase na carga é menor que 5,0 A.
O valor da resistência da impedância é menor que 60 Ω.
A potência aparente trifásica absorvida pela carga é maior que 6,5 kVA.
O valor, em módulo, da queda de tensão sobre a indutância da impedância é maior que 250 V.
Um aluno encontrou uma bobina e quis determinar o valor de sua resistência interna Rbob e de sua indutância Lbob. Para tanto, conectou em série com a bobina uma resistência Rs = 10 Ω. Ele ligou o conjunto num varivolt e aplicou nele uma tensão de 36 V, eficazes, em 60 Hz. Com um voltímetro, mediu a tensão sobre o resistor, obtendo Vs = 20 V e sobre a bobina, obtendo Vbob = 22,4 V. Com os resultados obtidos fez os cálculos e concluiu que:
A tensão fasorial do varivolt deve ser escrita como Vvar = 36 /+40° V.
A bobina possui uma indutância menor que 30 mH.
A resistência da bobina é maior que 8 Ω.
A potência dissipada pelo resistor Rs é igual a 50 W.
Adotando a tensão Vs como referência, o ângulo da impedância da bobina é menor que 60°.
Determine o valor de YT.

Assinale a alternativa que corresponde a reposta.
YT=1,567 S< -50,194°
YT=0,195 S< -50,194°
YT=10,65 S< -45,65°
YT=1,567 S< +50,194°
YT=0,195 S< +50,194°
Seja o circuito paralelo mostrado na figura. A corrente fornecida pela fonte é dada por ig(t) = 5. cos (8.105 t) A. Equacionando o circuito é correto afirmar:

A corrente que circula pelo capacitor está adiantada da corrente da fonte de um ângulo maior que 50°.
A susceptância equivalente do circuito é indutiva e tem valor maior que 0,08 s.
Na construção do circuito equivalente, o valor da resistência equivalente é menor que 5,0 Ω.
A tensão instantânea, de regime permanente, sobre o indutor é dada por vL(t) = 44,76 cos (8.105 t - 10,2°) V.
O valor, do módulo, da tensão vo é menor que 50 V.
A figura mostra um resistor R = 2 Ω ligado em série com uma impedância Z, desconhecida. Do circuito sabe-se que o fator de potência é atrasado e que a potência média absorvida P = 300 W. É correto afirmar que:

A queda de tensão fasorial sobre a impedância tem módulo menor que 110 V.
A impedância Z é composta por um único elemento, resistivo, de valor igual a 31,3 Ω.
A potência aparente absorvida pela impedância Z é maior que 400 VA.
A impedância Z pode ser composta por dois, ou mais elementos, ligados em série ou em paralelo.
O ângulo θ° da corrente é negativo e menor que 32°.
Uma carga, com impedância Zc, absorve de uma fonte de tensão senoidal de 120 V, eficazes, 12 kVA, com fator de potência 0,856. Para a carga, é correto afirmar que:
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.
A tensão fasorial do varivolt deve ser escrita como Vvar = 36 /+40° V.
A bobina possui uma indutância menor que 30 mH.
A resistência da bobina é maior que 8 Ω.
A potência dissipada pelo resistor Rs é igual a 50 W.
Adotando a tensão Vs como referência, o ângulo da impedância da bobina é menor que 60°.
Determine o valor de YT.

Assinale a alternativa que corresponde a reposta.
YT=1,567 S< -50,194°
YT=0,195 S< -50,194°
YT=10,65 S< -45,65°
YT=1,567 S< +50,194°
YT=0,195 S< +50,194°
Seja o circuito paralelo mostrado na figura. A corrente fornecida pela fonte é dada por ig(t) = 5. cos (8.105 t) A. Equacionando o circuito é correto afirmar:

A corrente que circula pelo capacitor está adiantada da corrente da fonte de um ângulo maior que 50°.
A susceptância equivalente do circuito é indutiva e tem valor maior que 0,08 s.
Na construção do circuito equivalente, o valor da resistência equivalente é menor que 5,0 Ω.
A tensão instantânea, de regime permanente, sobre o indutor é dada por vL(t) = 44,76 cos (8.105 t - 10,2°) V.
O valor, do módulo, da tensão vo é menor que 50 V.
A figura mostra um resistor R = 2 Ω ligado em série com uma impedância Z, desconhecida. Do circuito sabe-se que o fator de potência é atrasado e que a potência média absorvida P = 300 W. É correto afirmar que:

A queda de tensão fasorial sobre a impedância tem módulo menor que 110 V.
A impedância Z é composta por um único elemento, resistivo, de valor igual a 31,3 Ω.
A potência aparente absorvida pela impedância Z é maior que 400 VA.
A impedância Z pode ser composta por dois, ou mais elementos, ligados em série ou em paralelo.
O ângulo θ° da corrente é negativo e menor que 32°.
Uma carga, com impedância Zc, absorve de uma fonte de tensão senoidal de 120 V, eficazes, 12 kVA, com fator de potência 0,856. Para a carga, é correto afirmar que:
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.
YT=1,567 S< -50,194°
YT=0,195 S< -50,194°
YT=10,65 S< -45,65°
YT=1,567 S< +50,194°
YT=0,195 S< +50,194°
Seja o circuito paralelo mostrado na figura. A corrente fornecida pela fonte é dada por ig(t) = 5. cos (8.105 t) A. Equacionando o circuito é correto afirmar:

A corrente que circula pelo capacitor está adiantada da corrente da fonte de um ângulo maior que 50°.
A susceptância equivalente do circuito é indutiva e tem valor maior que 0,08 s.
Na construção do circuito equivalente, o valor da resistência equivalente é menor que 5,0 Ω.
A tensão instantânea, de regime permanente, sobre o indutor é dada por vL(t) = 44,76 cos (8.105 t - 10,2°) V.
O valor, do módulo, da tensão vo é menor que 50 V.
A figura mostra um resistor R = 2 Ω ligado em série com uma impedância Z, desconhecida. Do circuito sabe-se que o fator de potência é atrasado e que a potência média absorvida P = 300 W. É correto afirmar que:

A queda de tensão fasorial sobre a impedância tem módulo menor que 110 V.
A impedância Z é composta por um único elemento, resistivo, de valor igual a 31,3 Ω.
A potência aparente absorvida pela impedância Z é maior que 400 VA.
A impedância Z pode ser composta por dois, ou mais elementos, ligados em série ou em paralelo.
O ângulo θ° da corrente é negativo e menor que 32°.
Uma carga, com impedância Zc, absorve de uma fonte de tensão senoidal de 120 V, eficazes, 12 kVA, com fator de potência 0,856. Para a carga, é correto afirmar que:
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.

A corrente que circula pelo capacitor está adiantada da corrente da fonte de um ângulo maior que 50°.
A susceptância equivalente do circuito é indutiva e tem valor maior que 0,08 s.
Na construção do circuito equivalente, o valor da resistência equivalente é menor que 5,0 Ω.
A tensão instantânea, de regime permanente, sobre o indutor é dada por vL(t) = 44,76 cos (8.105 t - 10,2°) V.
O valor, do módulo, da tensão vo é menor que 50 V.
A figura mostra um resistor R = 2 Ω ligado em série com uma impedância Z, desconhecida. Do circuito sabe-se que o fator de potência é atrasado e que a potência média absorvida P = 300 W. É correto afirmar que:

A queda de tensão fasorial sobre a impedância tem módulo menor que 110 V.
A impedância Z é composta por um único elemento, resistivo, de valor igual a 31,3 Ω.
A potência aparente absorvida pela impedância Z é maior que 400 VA.
A impedância Z pode ser composta por dois, ou mais elementos, ligados em série ou em paralelo.
O ângulo θ° da corrente é negativo e menor que 32°.
Uma carga, com impedância Zc, absorve de uma fonte de tensão senoidal de 120 V, eficazes, 12 kVA, com fator de potência 0,856. Para a carga, é correto afirmar que:
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.

A queda de tensão fasorial sobre a impedância tem módulo menor que 110 V.
A impedância Z é composta por um único elemento, resistivo, de valor igual a 31,3 Ω.
A potência aparente absorvida pela impedância Z é maior que 400 VA.
A impedância Z pode ser composta por dois, ou mais elementos, ligados em série ou em paralelo.
O ângulo θ° da corrente é negativo e menor que 32°.
Uma carga, com impedância Zc, absorve de uma fonte de tensão senoidal de 120 V, eficazes, 12 kVA, com fator de potência 0,856. Para a carga, é correto afirmar que:
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.
A potência que realiza trabalho absorvida é menor que 10 kW.
A potência reativa absorvida tem valor menor que 6 kVAr.
Sua impedância possui valor igual 1,2 Ω, mas, não é possível afirmar se é capacitiva ou indutiva.
O ângulo da corrente que circula por ela é maior que 32°.
O valor de pico da corrente que circula é maior que 150 A.
Um sinal de tensão é dado por: v(t) = 250 sen (120.pi.t + 15°) V. Para o sinal, é correto afirmar que:
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.
O valor eficaz da tensão é, aproximadamente, igual a 144 V.
Sua equação equivalente cossenoidal é escrita por v(t) = 250.cos (120.pi.t - 75°) V.
A frequência angular do sinal é igual a 60 rad/s.
O valor instantâneo da tensão, no tempo t = 0, é igual a 250 V.
O deslocamento angular do sinal corresponde a um tempo igual a 1,3 ms.
A figura mostra um motor elétrico que, quando ligado numa rede elétrica, cuja tensão alternada é descrita por v(t) = 120 sen(314,16t + 80°) V, fica sujeito à corrente elétrica alternada, descrita por i(t) = 5 cos(314,16t – 60°) A. Qual das afirmativas abaixo está correta.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.

Um amperímetro digital ligado ao motor mostraria, em seu display, uma corrente igual a 3,535 A, caso fosse fabricado para funcionar em frequência igual a 50 Hz.
O defasamento angular entre os dois sinais é maior que 3,0 ms.
A equação instantânea da corrente está escrita de forma errada, pois, uma tensão senoidal não pode gerar uma corrente cossenoidal.
A corrente no motor atinge o primeiro valor máximo negativo no instante t1 positivo, equivalente a 220°.
Os valores máximos positivos dos sinais são coincidentes, em um determinado tempo.