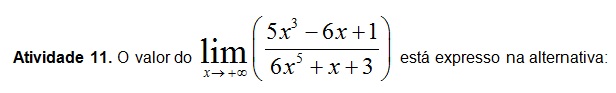CÁLCULO I

594/11
11/6
6/121
65/121
6/11
Determine o valor do limite %7D%7D%7D%7B%7B%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B4%7D%7D-%7B%7Bx%7D%7D%5E%7B%7B3%7D%7D%2B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7Bx%7D%2B%7B1%7D%5Cright)%7D%7D%7D) e, em seguida assinale a alternativa CORRETA:
e, em seguida assinale a alternativa CORRETA:
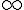
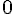
Sendo a derivada primeira da função %7D%7D%7D) dada por
dada por %7D.%7B%5Cleft(%7Bu%7D%27%5Cright)%7D) , de forma análoga, pode-se obter a derivada primeira da função
, de forma análoga, pode-se obter a derivada primeira da função %7D%7D%7D) . Assim, assinale a alternativa CORRETA que representa o resultado da derivada desta função.
. Assim, assinale a alternativa CORRETA que representa o resultado da derivada desta função.
%7D)
%7D)
%7D%7D%7D)
%7D)
%7D)
Seja y=f(x) uma função definida em 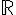 , tal que
, tal que 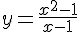 , com
, com 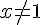 . Pela divisão polinomial da função racional apresentada tem-se que
. Pela divisão polinomial da função racional apresentada tem-se que 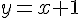 . Analise as afirmativas acerca do comportamento da função e em seguida assinale a alternativa CORRETA:
. Analise as afirmativas acerca do comportamento da função e em seguida assinale a alternativa CORRETA:
A imagem da função, aplicada a qualquer ponto do domínio sempre resultará em 2.
Quando o valor do domínio, aproxima-se de 1 pela esquerda, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se de 1 pela direita, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se a 1 pela esquerda, o valor da imagem da função aproxima-se de 2.
No ponto de restrição do domínio igual a 1, o valor da imagem da função é igual a 2.
Seja dada a função %7D.%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%5Cright)%7D) , utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
, utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
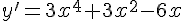
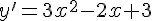
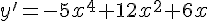
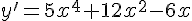
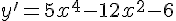
Determine o valor do limite 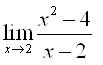 e em seguida, assinale a alternativa CORRETA.
e em seguida, assinale a alternativa CORRETA.
DICA: Utilize o método da fatoração.
-1
4
2
0
1
Ao resolver o limite %7D%7D%5E%7B%7B5%7D%7D) , utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
, utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
Assinale a alternativa CORRETA:
594/11
11/6
6/121
65/121
6/11
Determine o valor do limite %7D%7D%7D%7B%7B%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B4%7D%7D-%7B%7Bx%7D%7D%5E%7B%7B3%7D%7D%2B%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7Bx%7D%2B%7B1%7D%5Cright)%7D%7D%7D) e, em seguida assinale a alternativa CORRETA:
e, em seguida assinale a alternativa CORRETA:
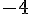
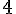
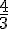
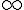
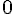
Sendo a derivada primeira da função %7D%7D%7D) dada por
dada por %7D.%7B%5Cleft(%7Bu%7D%27%5Cright)%7D) , de forma análoga, pode-se obter a derivada primeira da função
, de forma análoga, pode-se obter a derivada primeira da função %7D%7D%7D) . Assim, assinale a alternativa CORRETA que representa o resultado da derivada desta função.
. Assim, assinale a alternativa CORRETA que representa o resultado da derivada desta função.
%7D)
%7D)
%7D%7D%7D)
%7D)
%7D)
Seja y=f(x) uma função definida em 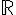 , tal que
, tal que 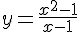 , com
, com 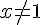 . Pela divisão polinomial da função racional apresentada tem-se que
. Pela divisão polinomial da função racional apresentada tem-se que 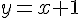 . Analise as afirmativas acerca do comportamento da função e em seguida assinale a alternativa CORRETA:
. Analise as afirmativas acerca do comportamento da função e em seguida assinale a alternativa CORRETA:
A imagem da função, aplicada a qualquer ponto do domínio sempre resultará em 2.
Quando o valor do domínio, aproxima-se de 1 pela esquerda, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se de 1 pela direita, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se a 1 pela esquerda, o valor da imagem da função aproxima-se de 2.
No ponto de restrição do domínio igual a 1, o valor da imagem da função é igual a 2.
Seja dada a função %7D.%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%5Cright)%7D) , utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
, utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
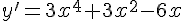
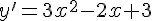
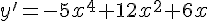
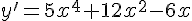
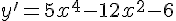
Determine o valor do limite 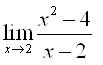 e em seguida, assinale a alternativa CORRETA.
e em seguida, assinale a alternativa CORRETA.
DICA: Utilize o método da fatoração.
-1
4
2
0
1
Ao resolver o limite %7D%7D%5E%7B%7B5%7D%7D) , utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
, utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
Assinale a alternativa CORRETA:
Sendo a derivada primeira da função %7D%7D%7D) dada por
dada por %7D.%7B%5Cleft(%7Bu%7D%27%5Cright)%7D) , de forma análoga, pode-se obter a derivada primeira da função
, de forma análoga, pode-se obter a derivada primeira da função %7D%7D%7D) . Assim, assinale a alternativa CORRETA que representa o resultado da derivada desta função.
. Assim, assinale a alternativa CORRETA que representa o resultado da derivada desta função.
%7D)
%7D)
%7D%7D%7D)
%7D)
%7D)
Seja y=f(x) uma função definida em  , tal que
, tal que 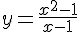 , com
, com 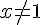 . Pela divisão polinomial da função racional apresentada tem-se que
. Pela divisão polinomial da função racional apresentada tem-se que 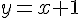 . Analise as afirmativas acerca do comportamento da função e em seguida assinale a alternativa CORRETA:
. Analise as afirmativas acerca do comportamento da função e em seguida assinale a alternativa CORRETA:
A imagem da função, aplicada a qualquer ponto do domínio sempre resultará em 2.
Quando o valor do domínio, aproxima-se de 1 pela esquerda, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se de 1 pela direita, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se a 1 pela esquerda, o valor da imagem da função aproxima-se de 2.
No ponto de restrição do domínio igual a 1, o valor da imagem da função é igual a 2.
Seja dada a função %7D.%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%5Cright)%7D) , utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
, utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
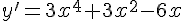
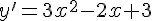
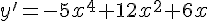
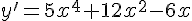
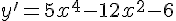
Determine o valor do limite 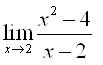 e em seguida, assinale a alternativa CORRETA.
e em seguida, assinale a alternativa CORRETA.
DICA: Utilize o método da fatoração.
-1
4
2
0
1
Ao resolver o limite %7D%7D%5E%7B%7B5%7D%7D) , utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
, utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
Assinale a alternativa CORRETA:
Seja y=f(x) uma função definida em 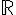 , tal que
, tal que 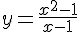 , com
, com 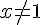 . Pela divisão polinomial da função racional apresentada tem-se que
. Pela divisão polinomial da função racional apresentada tem-se que 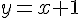 . Analise as afirmativas acerca do comportamento da função e em seguida assinale a alternativa CORRETA:
. Analise as afirmativas acerca do comportamento da função e em seguida assinale a alternativa CORRETA:
A imagem da função, aplicada a qualquer ponto do domínio sempre resultará em 2.
Quando o valor do domínio, aproxima-se de 1 pela esquerda, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se de 1 pela direita, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se a 1 pela esquerda, o valor da imagem da função aproxima-se de 2.
No ponto de restrição do domínio igual a 1, o valor da imagem da função é igual a 2.
Seja dada a função %7D.%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%5Cright)%7D) , utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
, utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
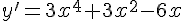
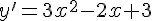
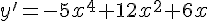
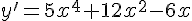
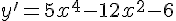
Determine o valor do limite 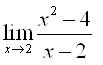 e em seguida, assinale a alternativa CORRETA.
e em seguida, assinale a alternativa CORRETA.
DICA: Utilize o método da fatoração.
-1
4
2
0
1
Ao resolver o limite %7D%7D%5E%7B%7B5%7D%7D) , utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
, utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
Assinale a alternativa CORRETA:
A imagem da função, aplicada a qualquer ponto do domínio sempre resultará em 2.
Quando o valor do domínio, aproxima-se de 1 pela esquerda, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se de 1 pela direita, o valor da imagem da função aproxima-se de 3.
Quando o valor do domínio, aproxima-se a 1 pela esquerda, o valor da imagem da função aproxima-se de 2.
No ponto de restrição do domínio igual a 1, o valor da imagem da função é igual a 2.
Seja dada a função %7D.%7B%5Cleft(%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D%2B%7B4%7D%5Cright)%7D) , utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
, utilizando a propriedade do produto, encontre a primeira derivada para esta função e, em seguida, assinale a alternativa CORRETA.
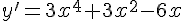
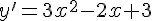
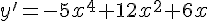
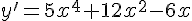
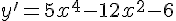
Determine o valor do limite 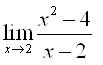 e em seguida, assinale a alternativa CORRETA.
e em seguida, assinale a alternativa CORRETA.
DICA: Utilize o método da fatoração.
-1
4
2
0
1
Ao resolver o limite %7D%7D%5E%7B%7B5%7D%7D) , utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
, utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
Assinale a alternativa CORRETA:
Determine o valor do limite 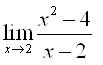 e em seguida, assinale a alternativa CORRETA.
e em seguida, assinale a alternativa CORRETA.
DICA: Utilize o método da fatoração.
-1
4
2
0
1
Ao resolver o limite %7D%7D%5E%7B%7B5%7D%7D) , utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
, utilizando os conceitos fundamentais e a definição, o valor determinado para a função no ponto de tendência indicado será?
Assinale a alternativa CORRETA:
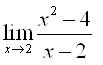 e em seguida, assinale a alternativa CORRETA.
e em seguida, assinale a alternativa CORRETA.-1
4
2
0
1